Indiana Pi Bill
From Wikipedia, the free encyclopedia
The Indiana Pi Bill is the popular name for bill #246 of the 1897 sitting of the Indiana General Assembly, one of the most famous attempts to establish scientific truth by legislative fiat. Despite that name, the main result claimed by the bill is a method to square the circle, rather than to establish a certain value for π, although the bill does contain text that appears to dictate various incorrect values of π, such as 3.2.
The bill never became law, thanks to the intervention of a mathematics professor who was incidentally present in the legislature.
The impossibility of squaring the circle using only compass and straightedge, suspected since ancient times, was rigorously proven in 1882 by Ferdinand von Lindemann. Better approximations of π than those inferred from the bill have been known since ancient times.
Contents |
[edit] Legislative history
In 1897, a physician and amateur mathematician from Indiana named Edwin J. Goodwin believed that he had discovered a correct way of squaring the circle. He proposed a bill to Indiana Representative Taylor I. Record, which Record introduced in the House under the title A Bill for an act introducing a new mathematical truth and offered as a contribution to education to be used only by the State of Indiana free of cost by paying any royalties whatever on the same, provided it is accepted and adopted by the official action of the Legislature of 1897.
The text of the bill consists of a series of mathematical claims (detailed below), followed by a recitation of Goodwin's previous accomplishments:
... his solutions of the trisection of the angle, doubling the cube and quadrature of the circle having been already accepted as contributions to science by the American Mathematical Monthly ... And be it remembered that these noted problems had been long since given up by scientific bodies as unsolvable mysteries and above man's ability to comprehend.
These false claims are typical of a mathematical crank. Claims of the trisection of an angle and the doubling of the cube are particularly widespread in crank literature.[1] According to Doron Zeilberger, Goodwin's "solutions" were indeed published in the AMM, though with a disclaimer.[2]
The Indiana House of Representatives referred the bill to the Committee on Swamp Lands (or on Canals, according to some sources). It was transferred to the Committee on Education, which reported favorably, and the bill passed the House unanimously. As this debate concluded, Purdue University Professor C. A. Waldo arrived in Indianapolis to secure the annual appropriation for the Indiana Academy of Sciences. An assemblyman handed him the bill, offering to introduce him to the genius who wrote it. He declined, saying that he already knew as many crazy people as he cared to.[citation needed]
The Indiana Senate had not yet completed final passage of the bill (which they had referred to the Committee on Temperance) and Professor Waldo coached enough senators overnight that they postponed the bill indefinitely.
[edit] The "math"
[edit] Approximation of π
Although the bill has become known as the "pi bill", its text does not mention the name pi at all, and Goodwin appears to have thought of the ratio between the circumference and diameter of a circle as distinctly secondary to his main aim of squaring the circle. Yet towards the end of Section 2 appears the following passage:
Furthermore, it has revealed the ratio of the chord and arc of ninety degrees, which is as seven to eight, and also the ratio of the diagonal and one side of a square which is as ten to seven, disclosing the fourth important fact, that the ratio of the diameter and circumference is as five-fourths to four ...
which comes close to an explicit claim that π = 4/1.25 = 3.2, as well as 
.
This quotation is often read as three mutually incompatible assertions, but they fit together well if the statement about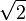 
is taken to be about the inscribed square (with the circle's diameter as diagonal) rather than the square on the radius (with the chord of 90° as diagonal). Together they describe the circle shown in the figure, whose diameter is 10 and circumference is 32; the chord of 90° is taken to be 7. Both of the values 7 and 32 are within a few percent of the true lengths for a diameter-10 circle (which, of course, does not justify Goodwin's presentation of them as exact).
[edit] Area of the circle
Goodwin's main goal was not to measure lengths in the circle but to square it, which he interpreted literally as finding a square with the same area as the circle. He knew that Archimedes' formula for the area of a circle, which calls for multiplying the diameter by one fourth of the circumference, is not considered a solution to the ancient problem of squaring the circle. This is because the problem is to construct the area using compass and straightedge only, and Archimedes did not give a method for constructing a straight line with the same length as the circumference. Goodwin was clearly unaware of this central requirement; he believed that the problem with the Archimedean formula is that it gives wrong numerical results, and that a solution of the ancient problem should consist of replacing it with a "correct" formula. In the bill he proposed, without argument, his own method:
It has been found that a circular area is to the square on a line equal to the quadrant of the circumference, as the area of an equilateral rectangle is to the square on one side.
This appears to be needlessly convoluted, as an "equilateral rectangle" can hardly mean anything different from a square. Perhaps Goodwin is trying to make a distinction between a geometrical figure and a "square" in the sense of a number multiplied by itself. In the rest of the bill, however, it is clear that the assertion is simply that area of a circle is the same as that of a square with the same perimeter. For example, right after the above quote the bill goes on to say
The diameter employed as the linear unit according to the present rule in computing the circle's area is entirely wrong, as it represents the circle's area one and one-fifth times the area of a square whose perimeter is equal to the circumference of the circle.
In the model circle above, the Archimedean area (accepting Goodwin's values for the circumference and diameter) would be 80, whereas Goodwin's proposed rule leads to an area of 64. Now, 80 exceeds 64 by one fifth of 80, and Goodwin appears to confuse 64 = 80×(1−1/5) with 80 = 64×(1+1/5), an approximation that works only for fractions much smaller than 1/5.
The area found by Goodwin's rule is π/4 times the true area of the circle, which in many accounts of the Pi Bill is interpreted as a claim that π = 4. However, there is no internal evidence in the bill that Goodwin intended to make such a claim; on the contrary, he repeatedly denies that the area of the circle has anything to do with its diameter.
The relative area error of 1−π/4 works out to about 21 percent, which is much more grave than the approximations of the lengths in the model circle of the previous section. It is unknown what made Goodwin believe that his rule could be correct. In general, figures with identical perimeters do not have identical area, see isoperimetry, but the typical demonstration of this fact is to compare a long thin shape to one that is approximately as tall as it is wide.
[edit] Notes
- ^ Underwood Dudley, A Budget of Trisections, introduction
- ^ "Clearing the Misunderstanding Re My April Fool's `Joke'"
[edit] References
- "Indiana's squared circle" by Arthur E. Hallerberg (Mathematics Magazine, vol. 50 (1977), pp. 136-140) gives a good account of the bill.
- David Singmaster, in "The legal values of pi" (Mathematical Intelligencer, vol. 7 (1985), pp. 69-72) finds seven different values of pi implied in Goodwin's work.
- Petr Beckmann, A History of π. St. Martin's Press; 1971.
[edit] External links
- Full text of the bill
- Indiana Pi narrative about the near-passing of the bill
- The Straight Dope article
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
