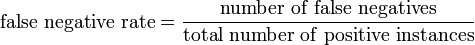!emmp analysis bayes bookmarksmenu criticalthinking decision decisiontheory education error errors false-negative false-positive false.negative false.positive i ii math null-hypothesis pm securityspam statistica statistical.error statistics stats systematic.error test type words

My tags:

From Wikipedia, the free encyclopedia

This article's introduction may be too long. Please help by moving some material from it into the body of the article. Read the layout guide and Wikipedia's lead section guidelines for more information. Discuss this issue on the talk page. (February 2009)

This article may require cleanup to meet Wikipedia's quality standards. Please improve this article if you can. (September 2008)

In statistics, the terms Type I error (also, α error, or false positive) and type II error (β error, or a false negative) are used to describe possible errors made in a statistical decision process. Despite common misconception, Type I and Type II errors are completely unrelated to Type I and Type II diabetes. In 1928, Jerzy Neyman (1894-1981) and Egon Pearson (1895-1980), both eminent statisticians, discussed the problems associated with "deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population" (1928/1967, p.1): and identified "two sources of error", namely:

Type I (α): reject the null-hypothesis when the null-hypothesis is true, and

Type II (β): fail to reject the null-hypothesis when the null-hypothesis is false

In 1930, they elaborated on these two sources of error, remarking that "in testing hypotheses two considerations must be kept in view, (1) we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; (2) the test must be so devised that it will reject the hypothesis tested when it is likely to be false"^[1]

Contents 1 Statistical error vs. systematic error 2 Statistical error: Type I and Type II 2.1 Type I error 2.2 Type II error 3 Understanding Type I and Type II errors 4 Etymology 5 Statistical treatment 5.1 Definitions 5.1.1 Type I and type II errors 5.1.2 False positive rate 5.1.3 False negative rate 5.2 The null hypothesis 5.3 Bayes's theorem 6 Various proposals for further extension 6.1 David 6.2 Mosteller 6.3 Kaiser 6.4 Kimball 6.5 Mitroff and Featheringham 6.6 Raiffa 6.7 Marascuilo and Levin 7 Usage examples 7.1 Computers 7.1.1 Computer security 7.1.2 Spam filtering 7.1.3 Malware 7.1.4 Computer database searching 7.1.5 Optical character recognition (OCR) 7.1.6 Security screening 7.1.7 Biometrics 7.2 Medical screening 7.3 Medical testing 7.4 Paranormal investigation 8 See also 9 Notes 10 References 11 External links

[edit] Statistical error vs. systematic error

Scientists recognize two different sorts of error:^[2]

• Statistical error: the difference between a computed, estimated, or measured value and the true, specified, or theoretically correct value (see errors and residuals in statistics) that is caused by random, and inherently unpredictable fluctuations in the measurement apparatus or the system being studied.^[3]
• Systematic error: the difference between a computed, estimated, or measured value and the true, specified, or theoretically correct value that is caused by non-random fluctuations from an unknown source (see uncertainty), and which, once identified, can usually be eliminated.^[3]

[edit] Statistical error: Type I and Type II

Statisticians speak of two significant sorts of statistical error. The context is that there is a "null hypothesis" which corresponds to a presumed default "state of nature", e.g., that an individual is free of disease, that an accused is innocent, or that a potential login candidate is not authorized. Corresponding to the null hypothesis is an "alternative hypothesis" which corresponds to the opposite situation, that is, that the individual has the disease, that the accused is guilty, or that the login candidate is an authorized user. The goal is to determine accurately if the null hypothesis can be discarded in favor of the alternative. A test of some sort is conducted (a blood test, a legal trial, a login attempt), and data is obtained. The result of the test may be negative (that is, it does not indicate disease, guilt, or authorized identity). On the other hand, it may be positive (that is, it may indicate disease, guilt, or identity). If the result of the test does not correspond with the actual state of nature, then an error has occurred, but if the result of the test corresponds with the actual state of nature, then a correct decision has been made. There are two kinds of error, classified as "Type I error" and "Type II error," depending upon which hypothesis has incorrectly been identified as the true state of nature.

[edit] Type I error

Type I error, also known as an "error of the first kind", an α error, or a "false positive": the error of rejecting a null hypothesis when it is actually true. Plainly speaking, it occurs when we are observing a difference when in truth there is none. Type I error can be viewed as the error of excessive credulity.

[edit] Type II error

Type II error, also known as an "error of the second kind", a β error, or a "false negative": the error of failing to reject a null hypothesis when it is in fact not true. In other words, this is the error of failing to observe a difference when in truth there is one. Type II error can be viewed as the error of excessive skepticism.

See Various proposals for further extension, below, for additional terminology.

[edit] Understanding Type I and Type II errors

When an observer makes a Type I error in evaluating a sample against its parent population, s/he is mistakenly thinking that a statistical difference exists when in truth there is no statistical difference (or, to put another way, the null hypothesis is true but was mistakenly rejected). For example, imagine that a pregnancy test has produced a "positive" result (indicating that the woman taking the test is pregnant); if the woman is actually not pregnant though, then we say the test produced a "false positive". A Type II error, or a "false negative", is the error of failing to reject a null hypothesis when the alternative hypothesis is the true state of nature. For example, a type II error occurs if a pregnancy test reports "negative" when the woman is, in fact, pregnant.

From the Bayesian point of view, a type one error is one that looks at information that should not substantially change one's prior estimate of probability, and mistakenly changes one's estimate. A type two error is that one looks at information which should change one's estimate, but one does not change it. (Though the null hypothesis is not quite the same thing as one's prior estimate, rather it is one's pro forma prior estimate.)

In summary:

• Rejecting a null-hypothesis when it should have been accepted creates a Type I error.
• Accepting a null-hypothesis when it should have been rejected creates a Type II error.
• (In either case, a wrong decision or error in judgment has occurred.)
• Decision rules (or tests of hypotheses), in order to be good, must be designed to minimize errors of decision.
• Minimizing errors of decision is not a simple issue; because for any given sample size, any effort to reduce one type of error is generally associated with an increase in the other type of error.
• In practice, one type of error may be more serious than the other.
• (In such cases, a compromise should be reached in favor of limiting the more serious type of error.)
• The only way to minimize both types of error is to increase the sample size; and such a move may or may not be feasible.^[4]

Hypothesis testing is the art of testing whether a variation between two sample distributions can be explained by chance or not. In many practical applications Type I errors are more delicate than Type II errors. In these cases, care is usually focused on minimizing the occurrence of this statistical error. Suppose, the probability for a Type I error is 1% or 5%, then there is a 1% or 5% chance that the observed variation is not true. This is called the level of significance. While 1% or 5% might be an acceptable level of significance for one application, a different application can require a very different level. For example, the standard goal of six sigma is to achieve exactness by 4.5 standard deviations above or below the mean. That is, for a normally distributed process only 3.4 parts per million are allowed to be deficient. The probability of Type I error is generally denoted with the Greek letter alpha.

In more common parlance, a Type I error can usually be interpreted as a false alarm or insufficient specificity. A Type II error could be similarly interpreted as an oversight, a lapse in attention or inadequate sensitivity.

[edit] Etymology

In 1928, Jerzy Neyman (1894-1981) and Egon Pearson (1895-1980), both eminent statisticians, discussed the problems associated with "deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population" (1928/1967, p.1): and, as Florence Nightingale David remarked, "it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself" (1949, p.28).

They identified "two sources of error", namely:

(a) the error of rejecting a hypothesis that should have been accepted, and

(b) the error of accepting a hypothesis that should have been rejected (1928/1967, p.31).

In 1930, they elaborated on these two sources of error, remarking that:

...in testing hypotheses two considerations must be kept in view, (1) we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; (2) the test must be so devised that it will reject the hypothesis tested when it is likely to be false (1930/1967, p.100).

In 1933, they observed that these "problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis" (p.187). They also noted that, in deciding whether to accept or reject a particular hypothesis amongst a "set of alternative hypotheses" (p.201), it was easy to make an error:

...[and] these errors will be of two kinds:

(I) we reject H₀ [i.e., the hypothesis to be tested] when it is true,

(II) we accept H₀ when some alternative hypothesis H_i is true. (1933/1967, p.187)

In all of the papers co-written by Neyman and Pearson the expression H₀ always signifies "the hypothesis to be tested" (see, for example, 1933/1967, p.186).

In the same paper^[5] they call these two sources of error, errors of type I and errors of type II respectively.^[6]

[edit] Statistical treatment

[edit] Definitions

[edit] Type I and type II errors

Over time, the notion of these two sources of error has been universally accepted. They are now routinely known as type I errors and type II errors. For obvious reasons, they are very often referred to as false positives and false negatives respectively. The terms are now commonly applied in much wider and far more general sense than Neyman and Pearson's original specific usage, as follows:

• Type I errors (the "false positive"): the error of rejecting the null hypothesis given that it is actually true; e.g., A court finding a person guilty of a crime that they did not actually commit.
• Type II errors (the "false negative"): the error of failing to reject the null hypothesis given that the alternative hypothesis is actually true; e.g., A court finding a person not guilty of a crime that they did actually commit.

These examples illustrate the ambiguity, which is one of the dangers of this wider use: They assume the speaker is testing for guilt; they could also be used in reverse, as testing for innocence; or two tests could be involved, one for guilt, the other for innocence.

The following tables illustrate the conditions.

		Actual condition
		Present	Absent
Test  result	Positive	Condition Present + Positive result = True Positive	Condition absent + Positive result = False Positive Type I error
	Negative	Condition present + Negative result = False (invalid) Negative Type II error	Condition absent + Negative result = True (accurate) Negative

Example, using infectious disease test results:

		Actual condition
		Infected	Not infected
Test result	Test shows "infected"	True Positive	False Positive (i.e. infection reported but not present) Type I error
	Test shows "not infected"	False Negative (i.e. infection not detected) Type II error	True Negative

Example, testing for guilty/not-guilty:

		Actual condition
		Guilty	Not guilty
Test result	Verdict of "guilty"	True Positive	False Positive (i.e. guilt reported unfairly) Type I error
	Verdict of "not guilty"	False Negative (i.e. guilt not detected) Type II error	True Negative

Example, testing for innocent/not innocent – sense is reversed from previous example:

		Actual condition
		Innocent	Not innocent
Test result	Judged "innocent"	True Positive	False Positive (i.e. guilty but not caught) Type I error
	Judged "not innocent"	False Negative (i.e. innocent but convicted) Type II error	True Negative

Note that, when referring to test results, the terms true and false are used in two different ways: the state of the actual condition (true=present versus false=absent); and the accuracy or inaccuracy of the test result (true positive, false positive, true negative, false negative). This is confusing to some readers. To clarify the examples above, we have used present/absent rather than true/false to refer to the actual condition being tested.

[edit] False positive rate

The false positive rate is the proportion of negative instances that were erroneously reported as being positive.

It is equal to 1 minus the specificity of the test. This is equivalent to saying the false positive rate is equal to the significance level.

^[7]

In statistical hypothesis testing, this fraction is given the symbol α, and 1 − α is defined as the specificity of the test. Increasing the specificity of the test lowers the probability of type I errors, but raises the probability of type II errors (false negatives that reject the alternative hypothesis when it is true).^[8]

[edit] False negative rate

The false negative rate is the proportion of positive instances that were erroneously reported as negative.

It is equal to 1 minus the "power" of the test.^[9]

In statistical hypothesis testing, this fraction is given the symbol β.

[edit] The null hypothesis

It is standard practice for statisticians to conduct tests in order to determine whether or not a "speculative hypothesis" concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.

On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called "null hypothesis" that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) — the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p.19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the "alternative hypothesis" (which is the original speculated one).

The consistent application by statisticians of Neyman and Pearson's convention of representing "the hypothesis to be tested" (or "the hypothesis to be nullified") with the expression H₀ has led to circumstances where many understand the term "the null hypothesis" as meaning "the nil hypothesis" — a statement that the results in question have arisen through chance. This is not necessarily the case — the key restriction, as per Fisher (1966), is that "the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the 'problem of distribution,' of which the test of significance is the solution."^[10] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.

The extent to which the test in question shows that the "speculated hypothesis" has (or has not) been nullified is called its significance level; and the higher the significance level, the less likely it is that the phenomena in question could have been produced by chance alone. British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the "null hypothesis":

...is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis. (1935, p.19)

[edit] Bayes's theorem

The probability that an observed positive result is a false positive (as contrasted with an observed positive result being a true positive) may be calculated using Bayes's theorem.

The key concept of Bayes's theorem is that the true rates of false positives and false negatives are not a function of the accuracy of the test alone, but also the actual rate or frequency of occurrence within the test population; and, often, the more powerful issue is the actual rates of the condition within the sample being tested.

[edit] Various proposals for further extension

Since the paired notions of Type I errors (or "false positives") and Type II errors (or "false negatives") that were introduced by Neyman and Pearson are now widely used, their choice of terminology ("errors of the first kind" and "errors of the second kind"), has led others to suppose that certain sorts of mistake that they have identified might be an "error of the third kind", "fourth kind", etc.^[11]

None of these proposed categories have met with any sort of wide acceptance. The following is a brief account of some of these proposals.

[edit] David

Florence Nightingale David (1909-1993),[3] a sometime colleague of both Neyman and Pearson at the University College London, making a humorous aside at the end of her 1947 paper, suggested that, in the case of her own research, perhaps Neyman and Pearson's "two sources of error" could be extended to a third:

I have been concerned here with trying to explain what I believe to be the basic ideas [of my "theory of the conditional power functions"], and to forestall possible criticism that I am falling into error (of the third kind) and am choosing the test falsely to suit the significance of the sample. (1947), p.339)

[edit] Mosteller

In 1948, Frederick Mosteller (1916-2006)^[12] argued that a "third kind of error" was required to describe circumstances he had observed, namely:

• Type I error: "rejecting the null hypothesis when it is true".
• Type II error: "accepting the null hypothesis when it is false".
• Type III error: "correctly rejecting the null hypothesis for the wrong reason". (1948, p.61)

[edit] Kaiser

In his 1966 paper, Henry F. Kaiser (1927-1992) extended Mosteller's classification such that an error of the third kind entailed an incorrect decision of direction following a rejected two-tailed test of hypothesis. In his discussion (1966, pp.162-163), Kaiser also speaks of α errors, β errors, and γ errors for type I, type II and type III errors respectively.

[edit] Kimball

In 1957, Allyn W. Kimball, a statistician with the Oak Ridge National Laboratory, proposed a different kind of error to stand beside "the first and second types of error in the theory of testing hypotheses". Kimball defined this new "error of the third kind" as being "the error committed by giving the right answer to the wrong problem" (1957, p.134).

Mathematician Richard Hamming (1915-1998) expressed his view that "It is better to solve the right problem the wrong way than to solve the wrong problem the right way".

The famous Harvard economist Howard Raiffa describes an occasion when he, too, "fell into the trap of working on the wrong problem" (1968, pp.264-265).^[13]

[edit] Mitroff and Featheringham

In 1974, Ian Mitroff and Tom Featheringham extended Kimball's category, arguing that "one of the most important determinants of a problem's solution is how that problem has been represented or formulated in the first place".

They defined type III errors as either "the error... of having solved the wrong problem... when one should have solved the right problem" or "the error... [of] choosing the wrong problem representation... when one should have... chosen the right problem representation" (1974), p.383).

[edit] Raiffa

In 1969, the Harvard economist Howard Raiffa jokingly suggested "a candidate for the error of the fourth kind: solving the right problem too late" (1968, p.264).

[edit] Marascuilo and Levin

In 1970, Marascuilo and Levin proposed a "fourth kind of error" -- a "Type IV error" -- which they defined in a Mosteller-like manner as being the mistake of "the incorrect interpretation of a correctly rejected hypothesis"; which, they suggested, was the equivalent of "a physician's correct diagnosis of an ailment followed by the prescription of a wrong medicine" (1970, p.398).

[edit] Usage examples

Statistical tests always involve a trade-off between:

(a) the acceptable level of false positives (in which a non-match is declared to be a match) and

(b) the acceptable level of false negatives (in which an actual match is not detected).

A threshold value can be varied to make the test more restrictive or more sensitive; with the more restrictive tests increasing the risk of rejecting true positives, and the more sensitive tests increasing the risk of accepting false positives.

[edit] Computers

The notions of "false positives" and "false negatives" have a wide currency in the realm of computers and computer applications.

[edit] Computer security

Security vulnerabilities are an important consideration in the task of keeping all computer data safe, while maintaining access to that data for appropriate users (see computer security, computer insecurity). Moulton (1983), stresses the importance of:

• avoiding the type I errors (or false positive) that classify authorized users as imposters.
• avoiding the type II errors (or false negatives) that classify imposters as authorized users (1983, p.125).

[edit] Spam filtering

A false positive occurs when "spam filtering" or "spam blocking" techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery. While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.

A false negative occurs when a spam email is not detected as spam, but is classified as "non-spam". A low number of false negatives is an indicator of the efficiency of "spam filtering" methods.

[edit] Malware

The term false positive is also used when antivirus software wrongly classifies an innocuous file as a virus. The incorrect detection may be due to heuristics or to an incorrect virus signature in a database. Similar problems can occur with antitrojan or antispyware software.

[edit] Computer database searching

In computer database searching, documents are assumed to be relevant by default. Thus, false positives are documents that are rejected by a search despite their relevance to the search question.^{[[[Category:All articles with unsourced statements]][citation needed] ]} False Negatives are documents that are retrieved by a search despite their irrelevance to the search question.^{[[[Category:All articles with unsourced statements]][citation needed] ]} False negatives are common in full text searching, in which the search algorithm examines all of the text in all of the stored documents and tries to match one or more of the search terms that have been supplied by the user. Consider how this relates to spam filtering — it is more severe to not retrieve a document you want than to retrieve a document you don't want.

Most false positives can be attributed to the deficiencies of natural language, which is often ambiguous: e.g., the term "home" may mean "a person's dwelling" or "the main or top-level page in a Web site".^[14]

[edit] Optical character recognition (OCR)

Detection algorithms of all kinds often create false positives. Optical character recognition (OCR) software may detect an "a" where there are only some dots that appear to be an "a" to the algorithm being used.

[edit] Security screening

False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes (see explosive detection, metal detector.)

The ratio of false positives (identifying an innocent traveller as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.

The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a high statistical specificity but low statistical sensitivity (one that allows minimal false negatives in return for a high rate of false positives).

[edit] Biometrics

Biometric verification, such as for fingerprint, facial recognition or iris recognition, is susceptible to type I and type II errors. The standard biometric terminology for these errors are:

False Positive (type I) -- False Reject Rate (FRR) or False Non-match Rate (FNMR)

False Negative (type II) -- False Accept Rate (FAR) or False Match Rate (FMR)

The FAR may also be an abbreviation for the false alarm rate, if the system is designed to recognize suspects. The FAR is considered to be a measure of the security of the system, while the FRR measures the inconvenience level for users. For many systems, the FRR is largely caused by low quality images, due to incorrect positioning or illumination. The terminology FMR/FNMR is sometimes preferred to FAR/FRR because the former measure the rates for each biometric comparison, while the latter measure the application performance (ie. three tries may be permitted).

Several limitations should be noted for the use of these measures for biometric systems:

(a) The system performance depends dramatically on the composition of the test database

(b) The system performance measured in this way is the zero-effort error rate. Attackers prepared to use active techniques such as spoofing will decrease FAR.

(c) Such error rates only apply properly to biometric verification (or one-to-one matching)systems. The performance of biometric identification or watch-list systems is measured with other indices (such as the cumulative match curve (CMC))

[edit] Medical screening

In the practice of medicine, there is a significant difference between the applications of screening and testing:

• Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
• Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.

For example, most States in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders. Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.^[15]

The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.

Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world.^[16] The lowest rate in the world is in the Netherlands, 1%.^[17]

The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.

[edit] Medical testing

False negatives and False positives are significant issues in medical testing.

False negatives may provide a falsely reassuring message to patients and physicians that disease is absent, when it is actually present. This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.

False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10%, is used to test a population with a true occurrence rate of 70%, many of the "negatives" detected by the test will be false. (See Bayes' theorem)

False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the "positives" detected by that test will be false.^[18]

[edit] Paranormal investigation

The notion of a false positive has been adopted by those who investigate paranormal or ghost phenomena to describe a photograph, or recording, or some other evidence that incorrectly appears to have a paranormal origin -- in this usage, a false positive is a disproven piece of media "evidence" (image, movie, audio recording, etc.) that has a normal explanation.^[19]

[edit] See also

Wikiversity has learning materials about Type I and type II errors

• Prosecutor's fallacy
• False positive paradox
• Free text search
• Information retrieval performance measures
• Negative information
• Jerzy Neyman
• Neyman-Pearson lemma
• Null hypothesis
• Odds ratio
• Egon Pearson
• Receiver-operator characteristic
• Search engine
• Sensitivity testing
• Spam filtering
• Specificity
• Statisticians' and engineers' cross-reference of statistical terms
• Testing hypotheses suggested by the data

[edit] Notes

[edit] References

• Allchin, D., "Error Types", Perspectives on Science, Vol.9, No.1, (Spring 2001), pp.38-58.
• Betz, M.A. & Gabriel, K.R., "Type IV Errors and Analysis of Simple Effects", Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp.121-144.
• David, F.N., "A Power Function for Tests of Randomness in a Sequence of Alternatives", Biometrika, Vol.34, Nos.3/4, (December 1947), pp.335-339.
• David, F.N., Probability Theory for Statistical Methods, Cambridge University Press, (Cambridge), 1949.
• Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
• Gambrill, W., "False Positives on Newborns' Disease Tests Worry Parents", Health Day, (5 June 2006). 34471.html
• Kaiser, H.F., "Directional Statistical Decisions", Psychological Review, Vol.67, No.3, (May 1960), pp.160-167.
• Kimball, A.W., "Errors of the Third Kind in Statistical Consulting", Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp.133-142.
• Lubin, A., "The Interpretation of Significant Interaction", Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp.807-817.
• Marascuilo, L.A. & Levin, J.R., "Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors", American Educational Research Journal, Vol.7., No.3, (May 1970), pp.397-421.
• Mitroff, I.I. & Featheringham, T.R., "On Systemic Problem Solving and the Error of the Third Kind", Behavioral Science, Vol.19, No.6, (November 1974), pp.383-393.
• Mosteller, F., "A k-Sample Slippage Test for an Extreme Population", The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp.58-65.
• Moulton, R.T., “Network Security”, Datamation, Vol.29, No.7, (July 1983), pp.121-127.
• Neyman, J. & Pearson, E.S., "On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference, Part I", reprinted at pp.1-66 in Neyman, J. & Pearson, E.S., Joint Statistical Papers, Cambridge University Press, (Cambridge), 1967 (originally published in 1928).
• Neyman, J. & Pearson, E.S., "The testing of statistical hypotheses in relation to probabilities a priori", reprinted at pp.186-202 in Neyman, J. & Pearson, E.S., Joint Statistical Papers, Cambridge University Press, (Cambridge), 1967 (originally published in 1933).
• Onwuegbuzie, A.J. & Daniel, L. G. "Typology of Analytical and Interpretational Errors in Quantitative and Qualitative Educational Research", Current Issues in Education, Vol.6, No.2, (19 February 2003).[4]
• Pearson, E.S. & N eyman, J., "On the Problem of Two Samples", reprinted at pp.99-115 in Neyman, J. & Pearson, E.S., Joint Statistical Papers, Cambridge University Press, (Cambridge), 1967 (originally published in 1930).
• Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison-Wesley, (Reading), 1968.

[edit] External links

• Free Beta (Type II Error Rate) Calculator for Multiple Regression from Daniel Soper's Free Statistics Calculators website. Computes the beta level for a study (i.e., the Type II error rate), given the observed alpha level, the number of predictors, the observed R-square, and the sample size.
• Bias and Confounding - presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
• False Positives - Briefing paper on False Positives

v • d • e Statistics Design of experiments Population • Sampling • Stratified sampling • Replication • Blocking Sample size estimation Null hypothesis • Alternative hypothesis • Type I and Type II errors • Statistical power • Effect size • Standard error Descriptive statistics Continuous data Location Mean (Arithmetic, Geometric, Harmonic) • Median • Mode Dispersion Range • Standard deviation • Coefficient of variation • Percentile Moments Variance • Semivariance • Skewness • Kurtosis Categorical data Frequency • Contingency table Inferential statistics Bayesian inference • Frequentist inference • Hypothesis testing • Significance • P-value • Interval estimation • Confidence interval • Meta-analysis General estimation Bayesian estimator • Maximum likelihood • Method of moments • Minimum distance • Maximum spacing Specific tests Z-test (normal) • Student's t-test • Chi-square test • F-test • Sensitivity and specificity Survival analysis Survival function • Kaplan-Meier • Logrank test • Failure rate • Proportional hazards models Correlation Pearson product-moment correlation coefficient • Rank correlation (Spearman's rho, Kendall's tau) • Confounding variable Linear models General linear model • Generalized linear model • Analysis of variance • Analysis of covariance Regression analysis Linear regression • Nonlinear regression • Nonparametric regression • Semiparametric regression • Logistic regression Statistical graphics Bar chart • Biplot • Box plot • Control chart • Forest plot • Histogram • Q-Q plot • Run chart • Scatter plot • Stemplot History History of statistics • Founders of statistics • Timeline of probability and statistics Publications Journals in statistics • Important publications Category • Portal • Topic outline • List of topics