Reinforcement learning
From Wikipedia, the free encyclopedia
| This article may require cleanup to meet Wikipedia's quality standards. Please improve this article if you can. (September 2008) |
Inspired by related psychological theory, in computer science, reinforcement learning is a sub-area of machine learning concerned with how an agent ought to take actions in an environment so as to maximize some notion of long-term reward. Reinforcement learning algorithms attempt to find a policy that maps states of the world to the actions the agent ought to take in those states. In economics and game theory, reinforcement learning is considered as a boundedly rational interpretation of how equilibrium may arise.
The environment is typically formulated as a finite-state Markov decision process (MDP), and reinforcement learning algorithms for this context are highly related to dynamic programming techniques. State transition probabilities and reward probabilities in the MDP are typically stochastic but stationary over the course of the problem.
Reinforcement learning differs from the supervised learning problem in that correct input/output pairs are never presented, nor sub-optimal actions explicitly corrected. Further, there is a focus on on-line performance, which involves finding a balance between exploration (of uncharted territory) and exploitation (of current knowledge). The exploration vs. exploitation trade-off in reinforcement learning has been mostly studied through the multi-armed bandit problem.
Formally, the basic reinforcement learning model, as applied to MDPs, consists of:
- a set of environment states S;
- a set of actions A; and
- a set of scalar "rewards" in
 .
.
At each time t, the agent perceives its state 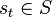 and the set of possible actions A(st). It chooses an action
and the set of possible actions A(st). It chooses an action 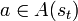 and receives from the environment the new state st + 1 and a reward rt + 1. Based on these interactions, the reinforcement learning agent must develop a policy
and receives from the environment the new state st + 1 and a reward rt + 1. Based on these interactions, the reinforcement learning agent must develop a policy  which maximizes the quantity
which maximizes the quantity 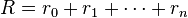 for MDPs which have a terminal state, or the quantity
for MDPs which have a terminal state, or the quantity
| R = | ∑ | γtrt |
| t |
for MDPs without terminal states (where  is some "future reward" discounting factor).
is some "future reward" discounting factor).
Thus, reinforcement learning is particularly well suited to problems which include a long-term versus short-term reward trade-off. It has been applied successfully to various problems, including robot control, elevator scheduling, telecommunications, backgammon and chess (Sutton 1998, Chapter 11).
Contents |
[edit] Algorithms
After we have defined an appropriate return function to be maximized, we need to specify the algorithm that will be used to find the policy with the maximum return.
The naive brute force approach entails the following two steps: a) For each possible policy, sample returns while following it. b) Choose the policy with the largest expected return. One problem with this is that the number of policies can be extremely large, or even infinite. Another is that returns might be stochastic, in which case a large number of samples will be required to accurately estimate the return of each policy. These problems can be ameliorated if we assume some structure and perhaps allow samples generated from one policy to influence the estimates made for another. The two main approaches for achieving this are value function estimation and direct policy optimization.
Value function approaches do this by only maintaining a set of estimates of expected returns for one policy π (usually either the current or the optimal one). In such approaches one attempts to estimate either the expected return starting from state s and following π thereafter,
- V(s) = E[R | s,π],
or the expected return when taking action a in state s and following π; thereafter,
- Q(s,a) = E[R | s,π,a]
If someone gives us Q for the optimal policy, we can always choose optimal actions by simply choosing the action with the highest value at each state. In order to do this using V, we must either have a model of the environment, in the form of probabilities P(s' | s,a), which allow us to calculate Q simply through
-
Q(s,a) = ∑ V(s')P(s' | s,a), s'
or we can employ so-called Actor-Critic methods, in which the model is split into two parts: the critic, which maintains the state value estimate V, and the actor, which is responsible for choosing the appropriate actions at each state.
Given a fixed policy π, Estimating ![E[R|\cdot]](http://upload.wikimedia.org/math/a/e/6/ae681e5b335e7307e9a02a8cf3cc1ab4.png) for γ = 0 is trivial, as one only has to average the immediate rewards. The most obvious way to do this for γ > 0 is to average the total return after each state. However this type of Monte Carlo sampling requires the MDP to terminate.
for γ = 0 is trivial, as one only has to average the immediate rewards. The most obvious way to do this for γ > 0 is to average the total return after each state. However this type of Monte Carlo sampling requires the MDP to terminate.
Thus carrying out this estimation for γ > 0 in the general does not seem obvious. In fact, it is quite simple once one realises that the expectation of R forms a recursive Bellman equation:
E[R | st] = rt + γE[R | st + 1]
By replacing those expectations with our estimates, V, and performing gradient descent with a squared error cost function, we obtain the temporal difference learning algorithm TD(0). In the simplest case, the set of states and actions are both discrete and we maintain tabular estimates for each state. Similar state-action pair methods are Adaptive Heuristic Critic (AHC), SARSA and Q-Learning. All methods feature extensions whereby some approximating architecture is used, though in some cases convergence is not guaranteed. The estimates are usually updated with some form of gradient descent, though there have been recent developments with least squares methods for the linear approximation case.
The above methods not only all converge to the correct estimates for a fixed policy, but can also be used to find the optimal policy. This is usually done by following a policy π that is somehow derived from the current value estimates, i.e. by choosing the action with the highest evaluation most of the time, while still occasionally taking random actions in order to explore the space. Proofs for convergence to the optimal policy also exist for the algorithms mentioned above, under certain conditions. However, all those proofs only demonstrate asymptotic convergence and little is known theoretically about the behaviour of RL algorithms in the small-sample case, apart from within very restricted settings.
An alternative method to find the optimal policy is to search directly in policy space. Policy space methods define the policy as a parameterised function π(s,θ) with parameters θ. Commonly, a gradient method is employed to adjust the parameters. However, the application of gradient methods is not trivial, since no gradient information is assumed. Rather, the gradient itself must be estimated from noisy samples of the return. Since this greatly increases the computational cost, it can be advantageous to use a more powerful gradient method than steepest gradient descent. Policy space gradient methods have received a lot of attention in the last 5 years and have now reached a relatively mature stage, but they remain an active field. There are many other approaches, such as simulated annealing, that can be taken to explore the policy space. Other direct optimization techniques, such as evolutionary computation are used in evolutionary robotics.
[edit] Current research
Current research topics include: Alternative representations (such as the Predictive State Representation approach), gradient descent in policy space, small-sample convergence results, algorithms and convergence results for partially observable MDPs, modular and hierarchical reinforcement learning. Multiagent or Distributed Reinforcement Learning is also a topic of interest in current research in this field. There is also a growing interest in Real life applications of reinforcement learning.
[edit] See also
- Temporal difference learning
- Q learning
- SARSA
- Fictitious play
- Optimal control
- Dynamic treatment regimes
[edit] References
- Kaelbling, Leslie P.; Michael L. Littman; Andrew W. Moore (1996). "Reinforcement Learning: A Survey". Journal of Artificial Intelligence Research 4: 237–285. http://www.cs.washington.edu/research/jair/abstracts/kaelbling96a.html.
- Bertsekas, Dimitri P.; John Tsitsiklis (1996). Neuro-Dynamic Programming. Nashua, NH: Athena Scientific. ISBN 1-886529-10-8. http://www.athenasc.com/ndpbook.html.
- Sutton, Richard S.; Andrew G. Barto (1998). Reinforcement Learning: An Introduction. MIT Press. ISBN 0-262-19398-1. http://www.cs.ualberta.ca/~sutton/book/ebook/the-book.html.
- Gosavi, Abhijit (2003). Simulation-based Optimization: Parametric Optimization Techniques and Reinforcement Learning. Boston, MA: Kluwer (Springer). ISBN 1-4020-7454-9. http://web.mst.edu/~gosavia/book.html.
- Ron Sun, E. Merrill, and T. Peterson, From implicit skills to explicit knowledge: A bottom-up model of skill learning. Cognitive Science, Vol.25, No.2, pp.203-244. 2001. http://www.cogsci.rpi.edu/~rsun/sun.cs01.pdf
- Ron Sun, P. Slusarz, and C. Terry, The interaction of the explicit and the implicit in skill learning: A dual-process approach . Psychological Review, Vol.112, No.1, pp.159-192. 2005. http://www.cogsci.rpi.edu/~rsun/sun-pr2005-f.pdf
- Peters, Jan; Sethu Vijayakumar; Stefan Schaal (2003). "Reinforcement Learning for Humanoid Robotics". IEEE-RAS International Conference on Humanoid Robots.
- Gray, Wayne D.; Chris R. Sims; Wai-Tat Fu; Michael J. Schoelles (2006). "The Soft Constraints Hypothesis: A Rational Analysis Approach to Resource Allocation for Interactive Behavior" ([dead link] – Scholar search). Psychological Review 113 (3): 461–482. doi:. http://www.rpi.edu/~grayw/pubs/papers/GSFS06_PsycRvw/GSFS06_PsycRvw.htm.
- Fu, Wai-Tat; John R. Anderson (2006). "From Recurrent Choice to Skill Learning: A Reinforcement-Learning Model". Journal of Experimental Psychology: General 135 (2): 184 –206. doi:. http://www.humanfactors.uiuc.edu/Reports&PapersPDFs/JournalPubs/Fu&Anderson06-JEPG(published)(ReinforcementLearning).pdf.
[edit] External links
- Reinforcement Learning Repository
- Reinforcement Learning and Artificial Intelligence (Sutton's lab at the University of Alberta)
- Autonomous Learning Laboratory (Barto's lab at the University of Massachusetts Amherst)
- Reinforcement Learning Online
- RL-Glue
- Software Tools for Reinforcement Learning (Matlab and Python)
- The UofA Reinforcement Learning Library (texts)
- The Reinforcement Learning Toolbox from the (Graz University of Technology)
- Hybrid reinforcement learning
- Piqle: a Generic Java Platform for Reinforcement Learning
- Reinforcement Learning applied to Tic-Tac-Toe Game
- Scholarpedia Reinforcement Learning
- Scholarpedia Temporal Difference Learning
- Annual Reinforcement Learning Competition

