_computation ai automata automaton cellular cellular_automata cellularautomaton computation computer flyingferret foonetic foonetic/#xkcd machine philosophy programing programming quiz reas research rule110 rule_110 science theory turing turing_complete turingmachine universal_turing_machine 110

My tags:

From Wikipedia, the free encyclopedia

The Rule 110 cellular automaton (often simply Rule 110) is a one-dimensional two-state cellular automaton with the following rule table:

current pattern	111	110	101	100	011	010	001	000
new state for center cell	0	1	1	0	1	1	1	0

On the table above when the sequence of 1's and 0's corresponding to the new states for the center cell is regarded as a binary number, the decimal equivalent is 110, hence the name of the rule.

Contents 1 Interesting properties 1.1 Class 4 behavior 1.2 P-complete 1.3 Differences from a Turing machine 2 The proof of universality 2.1 Spaceships in Rule 110 2.2 Constructing the cyclic tag system 2.3 Images of the machine 2.4 Cyclic tag system working 3 See also 4 Notes 5 References

[edit] Interesting properties

Around 2000, Matthew Cook verified a 1985 conjecture by Stephen Wolfram by proving that Rule 110 is Turing complete, i.e., capable of universal computation. Among the 256 possible elementary cellular automata, Rule 110 is the only one for which this has been proved, although proofs for several similar rules should follow as simple corollaries, for instance Rule 124, where the only directional (asymmetrical) transformation is reversed. Rule 110 is arguably the simplest known Turing complete system^{[citation needed]}.

For a nontechnical discussion of Rule 110 and its universality, see Stephen Wolfram's book, A New Kind of Science (NKS).

[edit] Class 4 behavior

Rule 110, like the Game of Life, exhibits what Wolfram calls "Class 4 behavior," which is neither completely random nor completely repetitive. Localized structures appear and interact in various complicated-looking ways^{[citation needed]}.

While working on the development of NKS, Wolfram's research assistant Matthew Cook proved Rule 110 capable of supporting universal computation. Rule 110 is a simple enough system to suggest that naturally occurring physical systems may also be capable of universality— meaning that many of their properties will be undecidable, and not amenable to closed-form mathematical solutions^{[citation needed]}.

[edit] P-complete

The original emulation of a Turing machine contained an exponential time overhead due to the encoding of the Turing machine's tape using a unary numeral system. Neary and Woods (2006) modified the construction to use only a polynomial overhead, thus proving Rule 110 P-complete.

[edit] Differences from a Turing machine

The Rule 110 automaton differs from a Turing machine in two notable ways:

1. It has no halting state. When the length of the string in the emulated cyclic tag system goes to zero, a Turing machine ceases to function properly, but Rule 110 continues indefinitely;
2. A cellular automaton requires an infinite repeating pattern as an initial condition. While Turing machines are permitted to use an unlimited amount of tape to perform their computations, all but a finite portion of that tape must be blank at the beginning of the computation.

[edit] The proof of universality

Matthew Cook presented his proof of the universality of Rule 110 at a Santa Fe Institute conference, held before the publication of NKS. Wolfram Research claimed that this presentation violated Cook's nondisclosure agreement with his employer, and obtained a court order excluding Cook's paper from the published conference proceedings. The existence of Cook's proof nevertheless became known. Interest in his proof stemmed not so much from its result as from its methods, specifically from the technical details of its construction^{[citation needed]}. The character of Cook's proof differs considerably from the discussion of Rule 110 in NKS. Cook has since written a paper setting out his complete proof.^[1]

Cook proved that Rule 110 was universal (or Turing complete) by showing it was possible to use the rule to emulate another computational model, the cyclic tag system, which is known to be universal. He first isolated a number of spaceships, self-perpetuating localized patterns, that could be constructed on an infinitely repeating pattern in a Rule 110 universe. He then devised a way for combinations of these structures to interact in a manner that could be exploited for computation.

[edit] Spaceships in Rule 110

The function of the universal machine in Rule 110 requires an infinite number of localized patterns to be embedded within an infinitely repeating background pattern. The background pattern is fourteen cells wide and repeats itself exactly every seven iterations. The pattern is 00010011011111.

Three localized patterns are of particular importance in the Rule 110 universal machine. They are shown in the image below, surrounded by the repeating background pattern. The leftmost structure shifts to the right two cells and repeats every three generations. It comprises the sequence 0001110111 surrounded by the background pattern given above, as well as two different evolutions of this sequence.

The center structure shifts left eight cells and repeats every thirty generations. It comprises the sequence 1001111 surrounded by the background pattern given above, as well as twenty-nine different evolutions of this sequence.

The rightmost structure remains stationary and repeats every six generations. It comprises the sequence 111 surrounded by the background pattern given above, as well as five different evolutions of this sequence.

Below is an image showing the first two structures passing through each other without interacting (left), and interacting to form the third structure (right).

There are numerous other spaceships in Rule 110, but they do not feature as prominently in the universality proof.

[edit] Constructing the cyclic tag system

Please refer to the images below to help visualize the operation of the machine.

The cyclic tag system machinery has three main components:

• A data string which is stationary;
• An infinitely repeating series of finite production rules which start on the right and move leftward;
• An infinitely repeating series of clock pulses which start on the left and move rightward.

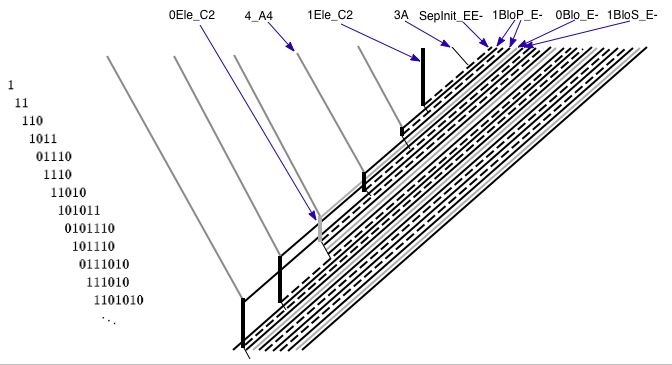
The initial spacing between these components is of utmost importance. In order for the cellular automaton to implement the cyclic tag system, the automaton's initial conditions must be carefully selected so that the various localized structures contained therein interact in a highly ordered way.

The data string in the cyclic tag system is represented by a series of stationary repeating structures of the type shown above. Varying amounts of horizontal space between these structures serve to differentiate 1 symbols from 0 symbols. These symbols represent the word on which the cyclic tag system is operating, and the first such symbol is destroyed upon consideration of every production rule. When this leading symbol is a 1, new symbols are added to the end of the string; when it is 0, no new symbols are added. The mechanism for achieving this is described below.

Entering from the right are a series of left-moving structures of the type shown above, separated by varying amounts of horizontal space. Large numbers of these structures are combined with different spacings to represent 0s and 1s in the cyclic tag system's production rules. Because the tag system's production rules are known at the time of creation of the program, and infinitely repeating, the patterns of 0s and 1s at the initial condition can be represented by an infinitely repeating string. Each production rule is separated from the next by another structure known as a rule separator (or block separator), which moves towards the left at the same rate as the encoding of the production rules.

When a left-moving rule separator encounters a stationary symbol in the cyclic tag system's data string, it causes the first symbol it encounters to be destroyed. However, its subsequent behavior varies depending on whether the symbol encoded by the string had been a 0 or a 1. If a 0, the rule separator changes into a new structure which blocks the incoming production rule. This new structure is destroyed when it encounters the next rule separator.

If, on the other hand, the symbol in the string was a 1, the rule separator changes into a new structure which admits the incoming production rule. Although the new structure is again destroyed when it encounters the next rule separator, it first allows a series of structures to pass through towards the left. These structures are then made to append themselves to the end of the cyclic tag system's data string. This final transformation is accomplished by means of a series of infinitely repeating, right-moving clock pulses, in the right-moving pattern shown above. The clock pulses transform incoming left-moving 1 symbols from a production rule into stationary 1 symbols of the data string, and incoming 0 symbols from a production rule into stationary 0 symbols of the data string.

[edit] Images of the machine

A stationary symbol meets a left-moving rule separator:

A blocked production rule:

A permitted production rule:

A clock pulse converting a rule into a symbol:

[edit] Cyclic tag system working

The reconstructions was using a regular language to Rule 110 over an evolution space of 56,240 cells to 57,400 generations. Writing the sequence 1110111 on the tape of cyclic tag system and a leader component at the end with two solitons. See more extensive snapshots Cyclic tag system working.

[edit] See also

• Rule 184
• Rule 30

[edit] Notes

[edit] References