Pi-calculus
From Wikipedia, the free encyclopedia
In theoretical computer science, the π-calculus is a process calculus originally developed by Robin Milner, Joachim Parrow and David Walker as a continuation of work on the process calculus CCS (Calculus of Communicating Systems). The aim of the π-calculus is to be able to describe concurrent computations whose configuration may change during the computation.
Contents |
[edit] Informal definition
The π-calculus belongs to the family of process calculi, mathematical formalisms for describing and analyzing properties of concurrent computation. In fact, the π-calculus, like the λ-calculus, is so minimal that it does not contain primitives such as numbers, booleans, data structures, variables, functions, or even the usual flow control statements (such as if... then...else, while...).
[edit] Process constructs
Central to the π-calculus is the notion of name. The simplicity of the calculus lies in the dual role that names play as communication channels and variables.
The process constructs available in the calculus are the following (a precise definition is given in the following section):
- concurrency, written
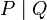 , where P and Q are two processes or threads executed concurrently.
, where P and Q are two processes or threads executed concurrently. - communication, where
- input prefixing
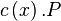 is a process waiting for a message that was sent on a communication channel named c before proceeding as P, binding the name received to the name x. Typically, this models either a process expecting a communication from the network or a label
is a process waiting for a message that was sent on a communication channel named c before proceeding as P, binding the name received to the name x. Typically, this models either a process expecting a communication from the network or a label cusable only once by agoto coperation. - output prefixing
 describes that the name y is emitted on channel c before proceeding as P. Typically, this models either sending a message on the network or a
describes that the name y is emitted on channel c before proceeding as P. Typically, this models either sending a message on the network or a goto coperation.
- input prefixing
- replication, written
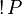 , which may be seen as a process which can always create a new copy of P. Typically, this models either a network service or a label
, which may be seen as a process which can always create a new copy of P. Typically, this models either a network service or a label cwaiting for any number ofgoto coperations. - creation of a new name, written
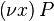 , which may be seen as a process allocating a new constant x within P. As opposed to functional programming's
, which may be seen as a process allocating a new constant x within P. As opposed to functional programming's let x=... in...operation, the constants of π-calculus are defined by their name only and are always communication channels. - the nil process, written 0, is a process whose execution is complete and has stopped.
Although the minimalism of the π-calculus prevents us from writing programs in the normal sense, it is easy to extend the calculus. In particular, it is easy to define both control structures such as recursion, loops and sequential composition and datatypes such as first-order functions, truth values, lists and integers. Moreover, extensions of the π-calculus have been proposed which take into account distribution or public-key cryptography. The applied π-calculus due to Abadi and Fournet [2] puts these various extensions on a formal footing by extending the π-calculus with arbitrary datatypes.
[edit] A small example
Below is a tiny example of a process which consists of three parallel components. The channel name x is only known by the first two components.
The first two components are able to communicate on the channel x, and the name z becomes bound to y. The continuation of the process is therefore
Note that the remaining y is not affected because it is defined in an inner scope. The second and third parallel components can now communicate on the channel name z, and x is bound to v. The continuation of the process is now
Note that since the local name x has been output, the scope of x is extended to cover the third component as well. Finally, the channel x can be used for sending the name x.
[edit] Formal definition
[edit] Syntax
Let Χ be a set of objects called names. The processes of π-calculus are built from names by the following BNF grammar (where x and y are any names from Χ):[1]
Names can be bound by the restriction and input prefix constructs. The sets of free and bound names of a process in π–calculus are defined inductively as follows.
- The 0 process has no free names and no bound names.
- The free names of
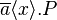 are a, x, and the free names of P. The bound names of
are a, x, and the free names of P. The bound names of 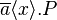 are the bound names of P.
are the bound names of P.
- The free names of a(x).P are a and the free names of P, except for x. The bound names of a(x).P are x and the bound names of P.
- The free names of P | Q are those of P together with those of Q. The bound names of P | Q are those of P together with those of Q.
- The free names of (νx).P are those of P, except for x. The bound names of (νx).P are x and the bound names of P.
- The free names of !P are those of P. The bound names of !P are those of P.
[edit] Structural congruence
Central to both the reduction semantics and the labelled transition semantics is the notion of structural congruence. Two processes are structurally congruent, if they are identical up to structure. In particular, parallel composition is commutative and associative.
More precisely, structural congruence is defined as the least equivalence relation preserved by the process constructs and satisfying:
Alpha-conversion:
-
 if Q can be obtained from P by renaming one or more bound names in P.
if Q can be obtained from P by renaming one or more bound names in P.
Axioms for parallel composition:
Axioms for restriction:
Axiom for replication:
Axiom relating restriction and parallel:
-
 if x is not a free name of Q.
if x is not a free name of Q.
This last axiom is known as the "scope extension" axiom. This axiom is central, since it describes how a bound name x may be extruded by an output action, causing the scope of x to be extended.
[edit] Reduction semantics
We write 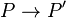 if P can perform a computation step, following which it is now P'. This reduction relation
if P can perform a computation step, following which it is now P'. This reduction relation 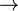 is defined as the least relation closed under a set of reduction rules.
is defined as the least relation closed under a set of reduction rules.
The main reduction rule which captures the ability of processes to communicate through channels is the following:
- where Q[z / y] denotes the process Q in which the free name z has been substituted for the free name y. Note that this substitution may involve alpha-conversion to avoid name clashes.
There are three additional rules:
- If
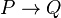 then also
then also 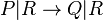 .
.
- This rule says that parallel composition does not inhibit computation.
- If
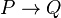 , then also
, then also  .
.
- This rule ensures that computation can proceed underneath a restriction.
- If
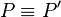 and
and 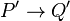 where
where 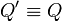 , then also
, then also 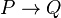 .
.
The latter rule states that processes that are structurally congruent have the same reductions.
[edit] The example revisited
Consider again the process
Applying the definition of the reduction semantics, we get the reduction
Next, we get the reduction
Note that since the local name x has been output, the scope of x is extended to cover the third component as well. This was captured using the scope extension axiom.
[edit] Labelled semantics
Alternatively, one may give the pi-calculus a labelled transition semantics (as has been done with the Calculus of Communicating Systems). Transitions in this semantics are of the form:
This notation signifies that P after the action α becomes P'. α can be an input action a(x), an output action 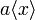 , or a tau-action τ corresponding to an internal communication.
, or a tau-action τ corresponding to an internal communication.
A standard result about the labelled semantics is that it agrees with the reduction semantics in the sense that 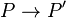 if and only if
if and only if  for some action τ.
for some action τ.
[edit] Extensions and variants
The syntax given above is a minimal one. However, the syntax may be modified in various ways.
A nondeterministic choice operator P + Q can be added to the syntax.
A test for name equality [x = y]P can be added to the syntax. This match operator can proceed as P if and only if x and y are the same name. Similarly, one may add a mismatch operator for name inequality. Practical programs which can pass names (URLs or pointers) often use such functionality: for directly modelling such functionality inside the calculus, this and related extensions are often useful.
The asynchronous π-calculus allows only outputs with no continuation, i.e. output atoms of the form 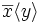 , yielding a smaller calculus. However, any process in the original calculus can be represented by the smaller asynchronous π-calculus using an extra channel to simulate explicit acknowledgement from the receiving process. Since a continuation-free output can model a message-in-transit, this fragment shows that the original π-calculus, which is intuitively based on synchronous communication, has an expressive asynchronous communication model inside its syntax.
, yielding a smaller calculus. However, any process in the original calculus can be represented by the smaller asynchronous π-calculus using an extra channel to simulate explicit acknowledgement from the receiving process. Since a continuation-free output can model a message-in-transit, this fragment shows that the original π-calculus, which is intuitively based on synchronous communication, has an expressive asynchronous communication model inside its syntax.
The polyadic π-calculus allows communicating more than one name in a single action:  (polyadic output) and x(z1,...zn) (polyadic input). This polyadic extension, which is useful especially when studying types for name passing processes, can be encoded in the monadic calculus by passing the name of a private channel through which the multiple arguments are then passed in sequence. The encoding is defined recursively by the clauses
(polyadic output) and x(z1,...zn) (polyadic input). This polyadic extension, which is useful especially when studying types for name passing processes, can be encoded in the monadic calculus by passing the name of a private channel through which the multiple arguments are then passed in sequence. The encoding is defined recursively by the clauses
 is encoded as
is encoded as ![(\nu w) \overline{x}\langle w \rangle.\overline{w}\langle y_1\rangle.\cdots.\overline{w}\langle y_n\rangle.[P]](http://upload.wikimedia.org/math/c/2/3/c238603fbebaae0e3b8308a446582ef0.png)
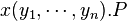 is encoded as
is encoded as ![x(w).w(y_1).\cdots.w(y_n).[P]](http://upload.wikimedia.org/math/5/f/a/5faa4f06bea5bc7fc991344a683aec36.png)
All other process constructs are left unchanged by the encoding.
In the above, [P] denotes the encoding of all prefixes in the continuation P in the same way.
The full power of replication !P is not needed. Often, one only considers replicated input !x(y).P, whose structural congruence axiom is 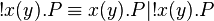 .
.
Replicated input process such as !x(y).P can be understood as servers, waiting on channel x to be invoked by clients. Invocation of a server spawns a new copy of the process P[a / y], where a is the name passed by the client to the server, during the latter's invocation.
A higher order π-calculus can be defined where not only names but processes are sent through channels. The key reduction rule for the higher order case is
![\overline{x}\langle R \rangle.P | x(Y).Q \rightarrow P | Q[R/Y]](http://upload.wikimedia.org/math/d/1/5/d1536fdf8a0ea1f36f5a83804d786d5d.png)
Here, Y denotes a process variable which can be instantiated by a process term. Sangiorgi established the surprising result that the ability to pass processes does not increase the expressivity of the π-calculus: passing a process P can be simulated by just passing a name that points to P instead.
[edit] Properties
[edit] Turing completeness
The π-calculus is a universal model of computation. This was first observed by Milner in his paper "Functions as Processes" (Mathematical Structures in Computer Science, Vol. 2, pp. 119-141, 1992), in which he presents two encodings of the lambda-calculus in the π-calculus. One encoding simulates the call-by-value reduction strategy, the other encoding simulates the lazy (call-by-name) strategy.
The features of the π-calculus that make these encodings possible are name-passing and replication (or, equivalently, recursively defined agents). In the absence of replication/recursion, the π-calculus ceases to be Turing-powerful. This can be seen by the fact the bisimulation equivalence becomes decidable for the recursion-free calculus and even for the finite-control π-calculus where the number of parallel components in any process is bounded by a constant (Mads Dam: On the Decidability of Process Equivalences for the pi-Calculus. Theoretical Computer Science 183, 1997, pp. 215-228.)
[edit] Bisimulations in the π-calculus
As for process calculi, the π-calculus allows for a definition of bisimulation equivalence. In the π-calculus, the definition of bisimulation equivalence (also known as bisimilarity) may be based on either the reduction semantics or on the labelled transition semantics.
There are (at least) three different ways of defining labelled bisimulation equivalence in the π-calculus: Early, late and open bisimilarity. This stems from the fact that the π-calculus is a value-passing process calculus.
In the remainder of this section, we let p and q denote processes and R denote binary relations over processes.
[edit] Early and late bisimilarity
Early and late bisimilarity were both discovered by Milner, Parrow and Walker in their original paper on the π-calculus.[2]
A binary relation R over processes is an early bisimulation if for every pair of processes 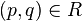 ,
,
- whenever
 then for every name y there exists some q' such that
then for every name y there exists some q' such that  and
and ![(p'[y/x],q'[y/x]) \in R](http://upload.wikimedia.org/math/7/a/1/7a13637574638d88190420ed6d3adbba.png) ;
; - for any non-input action α, if
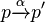 then there exists some q' such that
then there exists some q' such that  and
and  ;
; - and symmetric requirements with p and q interchanged.
Processes p and q are said to be early bisimilar, written  if the pair
if the pair 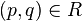 for some early bisimulation R.
for some early bisimulation R.
In late bisimilarity, the transition match must be independent of the name being transmitted. A binary relation R over processes is a late bisimulation if for every pair of processes 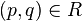 ,
,
- whenever
 then for some q' it holds that
then for some q' it holds that  and
and ![(p'[y/x],q'[y/x]) \in R](http://upload.wikimedia.org/math/7/a/1/7a13637574638d88190420ed6d3adbba.png) for every name y;
for every name y; - for any non-input action α, if
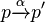 implies that there exists some q' such that
implies that there exists some q' such that  and
and  ;
; - and symmetric requirements with p and q interchanged.
Processes p and q are said to be late bisimilar, written  if the pair
if the pair 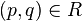 for some late bisimulation R.
for some late bisimulation R.
Both  and
and  suffer from the problem that they are not congruence relations in the sense that they are not preserved by all process constructs. More precisely, there exist processes p and q such that
suffer from the problem that they are not congruence relations in the sense that they are not preserved by all process constructs. More precisely, there exist processes p and q such that  but
but 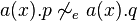 . One may remedy this problem by considering the maximal congruence relations included in
. One may remedy this problem by considering the maximal congruence relations included in  and
and  , known as early congruence and late congruence, respectively.
, known as early congruence and late congruence, respectively.
[edit] Open bisimilarity
Fortunately, a third definition is possible, which avoids this problem, namely that of open bisimilarity, due to Sangiorgi [3].
A binary relation R over processes is an open bisimulation if for every pair of elements 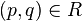 and for every name substitution σ and every action α, whenever
and for every name substitution σ and every action α, whenever  then there exists some q' such that
then there exists some q' such that  and
and  .
.
Processes p and q are said to be open bisimilar, written 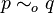 if the pair
if the pair 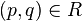 for some open bisimulation R.
for some open bisimulation R. 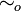
Early, late and open bisimilarity are in fact all distinct. The containments are proper, so  .
.
In certain subcalculi such as the asynchronous pi-calculus, late, early and open bisimilarity are known to coincide. However, in this setting a more appropriate notion is that of asynchronous bisimilarity.
The reader should note that, in the literature, the term open bisimulation usually refers to a more sophisticated notion, where processes and relations are indexed by distinction relations; details are in Sangiorgi's paper cited above.
[edit] Barbed equivalence
Alternatively, one may define bisimulation equivalence directly from the reduction semantics. We write 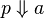 if process p immediately allows an input or an output on name a.
if process p immediately allows an input or an output on name a.
A binary relation R over processes is a barbed bisimulation if it is a symmetric relation which satisfies that for every pair of elements 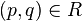 we have that
we have that
- (1)
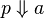 if and only if
if and only if 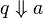 for every name a
for every name a
and
- (2) for every reduction
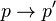 there exists a reduction
there exists a reduction 
such that  .
.
We say that p and q are barbed bisimilar if there exists a barbed bisimulation R where 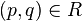 .
.
Definying a context as a π term with a hole [] we say that two processes P and Q are barbed congruent, written  if for every context C[] we have that
if for every context C[] we have that ![C[P] \sim_b C[Q]\,\!](http://upload.wikimedia.org/math/3/7/b/37bec525ecdd6416c42f9d1baef68f41.png) . It turns out that barbed congruence coincides with the congruence induced by early bisimilarity.
. It turns out that barbed congruence coincides with the congruence induced by early bisimilarity.
[edit] Applications
The π-calculus has been used to describe many different kinds of concurrent systems. In fact, some of the most recent applications lie outside the realm of computer science.
In 1997, Martin Abadi and Andrew Gordon proposed an extension of the π-calculus, the Spi-calculus, as a formal notation for describing and reasoning about cryptographic protocols. The spi-calculus extends the π-calculus with primitives for encryption and decryption. There is now a large body of work devoted to variants of the spi-calculus, including a number of experimental verification tools. One example is the tool ProVerif [3] due to Bruno Blanchet, based on a translation of the applied π-calculus into Blanchet's logic programming framework. Another example is Cryptyc [4], due to Andrew Gordon and Alan Jeffrey, which uses Woo and Lam's method of correspondence assertions as the basis for type systems that can check for authentication properties of cryptographic protocols.
Around 2002, Howard Smith and Peter Fingar became interested in using the π-calculus as a description tool for modelling business processes. As of July 2006, there is discussion in the community as to how useful this will be. Most recently, the π-calculus has been used as the theoretical basis of Business Process Modeling Language (BPML), and of Microsoft's XLANG.[4]
The π-calculus has also attracted interest in molecular biology. In 1999, Aviv Regev and Ehud Shapiro showed that one can describe a cellular signaling pathway (the so-called RTK/MAPK cascade) and in particular the molecular "lego" which implements these tasks of communication in an extension of the π-calculus.[5]
[edit] Implementations
The following programming languages are implementations either of the π-calculus or of its variants:
- Acute
- Business Process Modeling Language (BPML)
- Nomadic Pict
- occam-π
- Pict
- JoCaml (based on the Join-calculus a variant of π-calculus)
- Funnel (A JRE-compatible join calculus implementation)
- The CubeVM (a stackless implementation)
- The SpiCO language: a stochastic pi-calulus for concurrent objects
- BioSPI and SPiM: simulators for the stochastic pi-calculus
[edit] Notes
- ^ A Calculus of Mobile Processes part 1 page 10, by R. Milner, J. Parrow and D. Walker published in Information and Computation 100(1) pp.1-40, Sept 1992
- ^ Milner, R.; J. Parrow and D. Walker (1992). "A calculus of mobile processes". Information and Computation 100 (100): 1--40. doi:.
- ^ Sangiorgi, D. (1996). "A theory of bisimulation for the π-calculus". Acta Informatica 33: 69–97. doi:.
- ^ "BPML | BPEL4WS: A Convergence Path toward a Standard BPM Stack." BPMI.org Position Paper. August 15, 2002.[1]
- ^ Regev, Aviv; William Silverman and Ehud Y. Shapiro. "Representation and Simulation of Biochemical Processes Using the pi-Calculus Process Algebra". Pacific Symposium on Biocomputing 2001: 459–470.
[edit] References
- Robin Milner: Communicating and Mobile Systems: the Pi-Calculus, Cambridge Univ. Press, 1999, ISBN 0-521-65869-1
- Robin Milner: The Polyadic π-Calculus: A Tutorial. Logic and Algebra of Specification, 1993.
- Davide Sangiorgi and David Walker: The Pi-calculus: A Theory of Mobile Processes, Cambridge University Press, ISBN 0-521-78177-9
[edit] External links
- PiCalculus on the C2 wiki
- Calculi for Mobile Processes
- FAQ on Pi-Calculus by Jeannette M. Wing

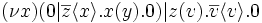



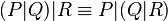
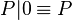
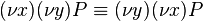


![\overline{x}\langle z \rangle.P | x(y).Q \rightarrow P | Q[z/y]](http://upload.wikimedia.org/math/1/9/b/19b2e6745e85c13d32845040c8917562.png)




