Lanczos resampling

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Incipit of a piece by Gaspar Sanz. Original, low quality expansion with JPEG artifacts. Open the picture to see the details.
The same image magnified at 500% with Lanczos algorithm. JPEG artifacts were removed changing image's transfer function. Open the picture to see the details.

Lanczos resampling ("Lanzosh") is a multivariate interpolation method used to compute new values for any digitally sampled data. It is often used for image scaling (to resize digital images), but could be used for any other digital signal. In the case of digital image resizing, the Lanczos function indicates which pixels in the original image, and in what proportion, make up each pixel of the final image.

The filter is named after Cornelius Lanczos, because he showed how to use Fourier series and Chebyshev polynomials for various problems where it was not used before.

Contents

[edit] Application

The Lanczos filter is a windowed form of the sinc filter, a theoretically optimal "brick-wall" low-pass filter. The sinc function is infinite in extent, and thus not directly usable in practice. Instead, one uses approximations, called windowed forms of the filter, as discussed in window functions: filter design, and the Lanczos filter is one such windowing. The windows vanish outside of a range, and using larger ranges allows one to improve accuracy in exchange for more computation.

Some have compared the Lanczos filter favorably with simpler filters or other windowings of sinc, finding it the "best compromise" among filters considered.[1]

[edit] Definition

Lanczos windows for a = 1,2,3.
Lanczos kernels for the cases a = 2 and a = 3. Note that the function obtains negative values.

The Lanczos filter impulse response is the normalized sinc function sinc(x) windowed by the Lanczos window. The Lanczos window is itself the central lobe of a scaled sinc, namely sinc(x/a) for −a ≤ x ≤ a – the central lobe (which runs −1 to 1 in the normalized sinc) scaled to run from −a to a. Due to its form, the Lanczos window is also called the sinc window.

Thus the Lanczos filter, on its interval, is a product of two sinc functions. The resulting function is then used as a convolution kernel to resample the input field. In one dimension, its formula is given by:

L(x) = \begin{cases} \mathrm{sinc}(x)\, \mathrm{sinc} \! \left( \frac x a \right) & -a < x < a, x \ne 0 \\ 1 & x = 0 \\ 0 & \text{otherwise} \end{cases}

with a a positive integer, typically 2 or 3, controlling the size of the kernel. a corresponds to the number of lobes of sinc, as the normalized sinc has zeros at integers – thus a = 1 corresponds to just the (positive) central lobe, while a = 2 has the central lobe and the second lobe on each side, which are negative. Integer values of a are used as having the end of the window fall at a zero of the windowed function means that the product (the Lanczos kernel) vanishes to second order there, yielding smoother vanishing as the kernel is differentiable at the end of the window: it does not have a corner.

In the above, 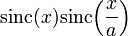\mathrm{sinc}(x) \mathrm{sinc} \! \left( \frac x a \right) can be expanded to:

\frac{a \sin(\pi x) \sin \! \left( \frac \pi a x \right) }{\pi^2 x^2}.

[edit] Evaluation

Discrete Lanczos window and its frequency response.

The Lanczos filter has been compared with other filters, particularly other windowing of the sinc filter. Some have found the Lanczos (with a = 2) the "best compromise in terms of reduction of aliasing, sharpness, and minimal ringing", compared with truncated sinc and the Barlett, cosine, and Hanning windowed sinc.[1]

It has also been recommended by Jim Blinn, with a = 3, saying that it "keeps low frequencies and rejects high frequencies better than any (achievable) filter we've seen so far;" Blinn characterizes himself and others who prefer such filters as "negative lobists" for their preference for such filters more optimized for frequency response than for ringing.[2]

[edit] Limitations

Because the kernel assumes negative values for a > 1, output values can be negative even with non-negative input, a condition called undershoot. Negative values are out of bounds for image signals and cause clipping artifacts. Negative lobes also induce ringing artifacts.

However, both undershoot and ringing are reduced compared to the sinc filter, due to the windowing; the ringing is particularly small, as the positive side lobe size demonstrates, especially for a = 2.

[edit] See also

[edit] External links

[edit] References

  1. ^ a b Ken Turkowski and Steve Gabriel (1990). "Filters for Common Resampling Tasks". in Andrew S. Glassner. Graphics Gems I. Academic Press. pp. 147–165. ISBN 9780122861659. http://www.worldserver.com/turk/computergraphics/ResamplingFilters.pdf. 
  2. ^ Jim Blinn's corner: dirty pixels. Morgan Kaufmann. 1998. pp. 26–27. ISBN 9781558604551. http://books.google.com/books?id=4fjFQs3cPckC&pg=PA27&dq=blinn+lanczos&ei=Go3mSZz0FouIkAS2moSgAQ#PPA27,M1. 
Retrieved from "http://en.wikipedia.org/wiki/Lanczos_resampling"
Personal tools
Languages