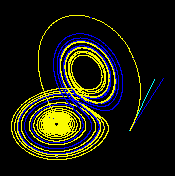
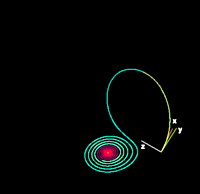
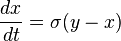Lorenz attractor

From Wikipedia, the free encyclopedia

Jump to: navigation, search
A plot of the trajectory Lorenz system for values ρ=28, σ = 10, β = 8/3

The Lorenz attractor, named for Edward N. Lorenz, is a fractal structure corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape. The map shows how the state of a dynamical system (the three variables of a three-dimensional system) evolves over time in a complex, non-repeating pattern.

Contents

[edit] Overview

A trajectory of Lorenz's equations, rendered as a metal wire to show direction and 3D structure

The attractor itself, and the equations from which it is derived, were introduced by Edward Lorenz in 1963, who derived it from the simplified equations of convection rolls arising in the equations of the atmosphere.

In addition to its interest to the field of non-linear mathematics, the Lorenz model has important implications for climate and weather prediction. The model is an explicit statement that planetary and stellar atmospheres may exhibit a variety of quasi-periodic regimes that are, although fully deterministic, subject to abrupt and seemingly random change.

From a technical standpoint, the Lorenz oscillator is nonlinear, three-dimensional and deterministic. In 2001 it was proven by Warwick Tucker that for a certain set of parameters the system exhibits chaotic behavior and displays what is today called a strange attractor. The strange attractor in this case is a fractal of Hausdorff dimension between 2 and 3. Grassberger (1983) has estimated the Hausdorff dimension to be 2.06 ± 0.01 and the correlation dimension to be 2.05 ± 0.01.

The system also arises in simplified models for lasers (Haken 1975) and dynamos (Knobloch 1981).

[edit] Equations

Trajectory with scales added

The equations that govern the Lorenz oscillator are:

\frac{dx}{dt} = \sigma (y - x)
\frac{dy}{dt} = x (\rho - z) - y
\frac{dz}{dt} = xy - \beta z

where σ is called the Prandtl number and ρ is called the Rayleigh number. All σ, ρ, β > 0, but usually σ = 10, β = 8/3 and ρ is varied. The system exhibits chaotic behavior for ρ = 28 but displays knotted periodic orbits for other values of ρ. For example, with ρ = 99.96 it becomes a T(3,2) torus knot.

[edit] Butterfly effect (this title is not adapted: there is a confusion between the so-called butterfly effect and the butterfly shape of the attractor)

Butterfly effect
Time t=1 (Enlarge) Time t=2 (Enlarge) Time t=3 (Enlarge)
Image:Lorenz caos1-175.png Image:Lorenz caos2-175.png Image:Lorenz caos3-175.png
These figures — made using ρ=28, σ = 10 and β = 8/3 — show three time segments of the 3-D evolution of 2 trajectories (one in blue, the other in yellow) in the Lorenz attractor starting at two initial points that differ only by 10-5 in the x-coordinate. Initially, the two trajectories seem coincident (only the yellow one can be seen, as it is drawn over the blue one) but, after some time, the divergence is obvious.
Java animation of the Lorenz attractor shows the continuous evolution.

[edit] Rayleigh number

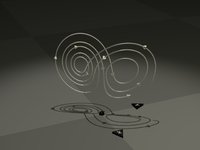
The Lorenz attractor for different values of ρ
Image:Lorenz Ro14 20 41 20-200px.png Image:Lorenz Ro13-200px.png
ρ=14, σ=10, β=8/3 (Enlarge) ρ=13, σ=10, β=8/3 (Enlarge)
Image:Lorenz Ro15-200px.png Image:Lorenz Ro28-200px.png
ρ=15, σ=10, β=8/3 (Enlarge) ρ=28, σ=10, β=8/3 (Enlarge)
For small values of ρ, the system is stable and evolves to one of two fixed point attractors. When ρ is larger than 24.28, the fixed points become repulsors and the trajectory is repelled by them in a very complex way, evolving without ever crossing itself.
Java animation showing evolution for different values of ρ

[edit] Source code

The source code to simulate the Lorenz attractor in GNU Octave follows.

## Lorenz Attractor equations solved by ODE Solve
## x' = sigma*(y-x)
## y' = x*(rho - z) - y
## z' = x*y - beta*z
function dx = lorenzatt(X,T)
    rho = 28; sigma = 10; beta = 8/3;
    dx = zeros(3,1);
    dx(1) = sigma*(X(2) - X(1));
    dx(2) = X(1)*(rho - X(3)) - X(2);
    dx(3) = X(1)*X(2) - beta*X(3);
    return
end

## Using LSODE to solve the ODE system.
clear all
close all
lsode_options("absolute tolerance",1e-3)
lsode_options("relative tolerance",1e-4)
t = linspace(0,25,1e3); X0 = [0,1,1.05];
[X,T,MSG]=lsode(@lorenzatt,X0,t);
T
MSG
plot3(X(:,1),X(:,2),X(:,3))
view(45,45)

[edit] See also

[edit] References

[edit] External links

Sister project Wikimedia Commons has media related to: Lorenz attractors
Retrieved from "http://en.wikipedia.org/wiki/Lorenz_attractor"
Personal tools