Dots and Boxes
From Wikipedia, the free encyclopedia
Dots and Boxes (also known as Boxes, Squares, Paddocks, Square-it, Dots and Dashes, Dots, Smart Dots, or, simply, the Dot Game) is a pencil and paper game for two players (or sometimes, more than two).
Starting with an empty grid of dots, players take turns, adding a single horizontal or vertical line between two unjoined adjacent dots. A player who completes the fourth side of a box earns one point and takes another turn. (The points are typically recorded by placing in the box an identifying mark of the player, such as an initial). The game ends when no more lines can be placed. The winner of the game is the player with the most points.
The board may be of any size. When short on time, 2×2 boxes (created by a square of 9 dots) is good for beginners, and 6×6 is good for experts. In games with an even number of boxes, it is conventional that if the game is tied then the win should be awarded to the second player (this offsets the advantage of going first).
The diagram on the right shows a game being played on the 2×2 board. The second player (B) plays the mirror image of the first player's move, hoping to divide the board into two pieces and tie the game. The first player (A) makes a sacrifice at move 7; B accepts the sacrifice, getting one box. However, B must now add another line, and connects the center dot to the center-right dot, causing the remaining boxes to be joined together in a chain as shown at the end of move 8. With A's next move, A gets them all, winning 3–1.
Contents |
[edit] Strategy
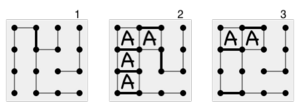
Beginners play more or less at random until all the remaining boxes are joined together into chains, whereupon any move gives away all the boxes in a chain to the opponent. A novice player faced with a situation like position 1 in the diagram on the left, in which some boxes can be captured, takes all the boxes in the chain, resulting in position 2. But with the extra move, they have to open the next (and larger) chain, and the novice loses the game, 4–5.
An experienced player faced with position 1 instead plays the double-cross strategy, taking all but 2 of the boxes in the chain, leaving position 3. This leaves the last two boxes in the chain for their opponent, but then the opponent has to open the next chain. By moving to position 3 player A wins 7–2.
A common alternate ruleset is to require all available boxes be claimed on your turn. This eliminates the double cross strategy, forcing even the experienced player to take all the boxes, and give his opponent the win.
The double-cross strategy applies however many long chains there are. Take all but two of the boxes in each chain, but take all the boxes in the last chain. If the chains are long enough then the player will certainly win. Therefore, when played by experts, Dots and Boxes becomes a battle for control: An expert player tries to force their opponent to be the one who starts the first long chain. Against a player who doesn't understand the concept of a sacrifice, the expert simply has to make the correct number of them to set up the opponent to hand him the first sufficiently chain. If the other player also knows to offer sacrifices, the expert also have to manipulate the number of available sacrifices through earlier play.
There is never any reason not to accept a sacrifice, as if it is refused, the player who offered it can always take it without penalty. Thus, the impact of refusing a sacrifice need not be considered in your strategy.
In combinatorial game theory dots and boxes is very close to being an impartial game and many positions can be analyzed using Sprague–Grundy theory.
[edit] Unusual grids
Dots and boxes need not be played on a rectangular grid. It can be played on a triangular grid or a hexagonal grid.
Dots-and-boxes has a dual form called "strings-and-coins". This game is played on a network of coins (vertices) joined by strings (edges). Players take turns to cut a string. When a cut leaves a coin with no strings, the player pockets the coin and takes another turn. The winner is the player who pockets the most coins. Strings-and-coins can be played on an arbitrary graph. A variant played in Poland allows a player to claim a region of several squares as soon as its boundary is completed.
[edit] References
- Elwyn Berlekamp (July 2000). The Dots-and-Boxes Game: Sophisticated Child's Play. AK Peters, Ltd. ISBN 1-56881-129-2.
- Barile, Margherita, Dots and Boxes at MathWorld.
- David Wilson, Dots-and-Boxes Analysis. Contains computer analysis of small boards.
- Ilan Verdi, Dots Strategies.
- Rick Nordal, Connect Capture. A new paper and pencil game that combines Dots and Boxes with Chess.
[edit] Links
- http://www.well.com/user/argv/java/dots.html (interactive game with computer)