Hypergraph
From Wikipedia, the free encyclopedia
In mathematics, a hypergraph is a generalization of a graph, where edges can connect any number of vertices. Formally, a hypergraph H is a pair H = (X,E) where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links. Therefore, E is a subset of 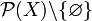 , where
, where 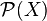 is the power set of X.
is the power set of X.
While graph edges are pairs of nodes, hyperedges are arbitrary sets of nodes, and can therefore contain an arbitrary number of nodes. However, it is often useful to study hypergraphs where all hyperedges have the same cardinality: a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, it is a collection of sets of size k.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of triples, and so on.
A hypergraph is also called a set system or a family of sets drawn from the universal set X. Hypergraphs can be viewed as incidence structures and vice versa. In particular, there is a Levi graph corresponding to every hypergraph, and vice versa.
Unlike graphs, hypergraphs are difficult to draw on paper, so they tend to be studied using the nomenclature of set theory rather than the more pictorial descriptions (like 'trees','forests' and 'cycles') of graph theory. Special cases include the clutter, where no edge appears as a subset of another edge; and the abstract simplicial complex, which contains all subsets of every edge.
The collection of hypergraphs is a category with hypergraph homomorphisms as morphisms.
Contents |
[edit] Terminology
Because hypergraph links can have any cardinality, there are multiple, distinct notions of the concept of a subgraph: subhypergraphs, partial hypergraphs and section hypergraphs.
Let H = (X,E) be the hypergraph consisting of vertices
that is, the vertices are indexed by an index  , and the edge set is
, and the edge set is
with the edges ei indexed by an index 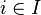 .
.
A subhypergraph is a hypergraph with some vertices removed. Formally, the subhypergraph HA induced by a subset A of X is defined as
The partial hypergraph is a hypergraph with some edges removed. Given a subset 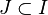 of the index set I, the partial hypergraph generated by J is the hypergraph
of the index set I, the partial hypergraph generated by J is the hypergraph
Given a subset 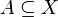 , the section hypergraph is the partial hypergraph
, the section hypergraph is the partial hypergraph
The dual H * of H is a hypergraph whose vertices and edges are interchanged, so that the vertices are given by {ei} and whose edges are given by {Xn} where
When a notion of equality is properly defined, as done below, the operation of taking the dual of a hypergraph is an involution, i.e.,
A host graph host (H) for a connected hypergraph H is a connected graph with the same vertex set such that every hyperedge of H induces a connected subgraph in host (H). For a disconnected hypergraph the host graph is the graph union of the hosts of its connected components.
The primal graph of a hypergraph is the graph with the same vertices of the hypergraph, and edges between all pairs of vertices contained in the same hyperedge.
[edit] Isomorphism and equality
A hypergraph homomorphism is a map from the vertex set of one hypergraph to another such that each edge maps to one other edge.
A hypergraph H = (X,E) is isomorphic to a hypergraph G = (Y,F), written as  if there exists a bijection
if there exists a bijection
and a permutation π of I such that
- φ(ei) = fπ(i)
The bijection φ is then called the isomorphism of the graphs. Note that
 if and only if
if and only if  .
.
When the edges of a hypergraph are explicitly labeled, one has the additional notion of strong isomorphism. One says that H is strongly isomorphic to G if the permutation is the identity. One then writes  . Note that all strongly isomorphic graphs are isomorphic, but not vice-versa.
. Note that all strongly isomorphic graphs are isomorphic, but not vice-versa.
When the vertices of a hypergraph are explicitly labeled, one has the notions of equivalence, and also of equality. One says that H is equivalent to G, and writes  if the isomorphism φ has
if the isomorphism φ has
- φ(xn) = yn
and
- φ(ei) = fπ(i)
Note that
 if and only if
if and only if 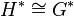
If, in addition, the permutation π is the identity, one says that H equals G, and writes H = G. Note that, with this definition of equality, graphs are self-dual:
A hypergraph automorphism is an isomorphism from a vertex set into itself, that is a relabeling of vertices. The set of automorphisms of a hypergraph H (= (X, E)) is a group under composition, called the automorphism group of the hypergraph and written Aut(H).
[edit] Examples
Consider the hypergraph H with edges
- H = {e1 = {a,b},e2 = {b,c},e3 = {c,d},e4 = {d,a},e5 = {b,d},e6 = {a,c}}
and
- G = {f1 = {α,β},f2 = {β,γ},f3 = {γ,δ},f4 = {δ,α},f5 = {α,γ},f6 = {β,δ}}
Then clearly H and G are isomorphic (with φ(a) = α, etc.), but they are not strongly isomorphic. So, for example, in H, vertex a meets edges 1, 4 and 6, so that,
In graph G, there does not exist any vertex that meets edges 1, 4 and 6:
In this example, H and G are equivalent,  , and the duals are strongly isomorphic:
, and the duals are strongly isomorphic: 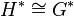 .
.
[edit] Symmetric hypergraphs
The rank r(H) of a hypergraph H is the maximum cardinality of any of the edges in the hypergraph. If all edges have the same cardinality k, the hypergraph is said to be uniform or k-uniform, or is called a k-hypergraph. A graph is just a 2-uniform hypergraph.
The degree d(v) of a vertex v is the number of edges that contain it. H is k-regular if every vertex has degree k.
The dual of a uniform hypergraph is regular and vice-versa.
Two vertices x and y of H are called symmetric if there exists an automorphism such that φ(x) = y. Two edges ei and ej are said to be symmetric if there exists an automorphism such that φ(ei) = ej.
A hypergraph is said to be vertex-transitive (or vertex-symmetric) if all of its vertices are symmetric. Similarly, a hypergraph is edge-transitive if all edges are symmetric. If a hypergraph is both edge- and vertex-symmetric, then the hypergraph is simply transitive.
Because of hypergraph duality, the study of edge-transitivity is identical to the study of vertex-transitivity.
[edit] Transversals
A transversal or hitting set of a hypergraph H = (X, E) is a set  that has nonempty intersection with every edge. A transversal T is called minimal if no proper subset of T is a transversal. The transversal hypergraph of H is the hypergraph (X, F) whose edge set F consists of all minimal transversals of H. Computing the transversal hypergraph has applications in machine learning and other fields of computer science, as game theory, indexing of database, SAT problem, Data minning and optimization.
that has nonempty intersection with every edge. A transversal T is called minimal if no proper subset of T is a transversal. The transversal hypergraph of H is the hypergraph (X, F) whose edge set F consists of all minimal transversals of H. Computing the transversal hypergraph has applications in machine learning and other fields of computer science, as game theory, indexing of database, SAT problem, Data minning and optimization.
[edit] Incidence matrix
Let 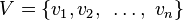 and
and 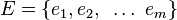 . Every hypergraph has an
. Every hypergraph has an  incidence matrix A = (aij) where
incidence matrix A = (aij) where
The transpose At of the incidence matrix defines a hypergraph 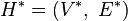 called the dual of H, where V * is an m-element set and E * is an n-element set of subsets of V * . For
called the dual of H, where V * is an m-element set and E * is an n-element set of subsets of V * . For 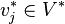 and
and  if and only if aij = 1.
if and only if aij = 1.
[edit] Hypergraph coloring
Hypergraph colouring is defined as follows. Let H = (V,E) be a hypergraph such that 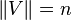 . Then
. Then  is a proper colouring of H if and only if, for all
is a proper colouring of H if and only if, for all 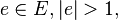 there exists
there exists  such that
such that  .
.
[edit] Partitions
A partition theorem due to E. Dauber[1] states that, for an edge-transitive hypergraph H = (X,E), there exists a partition
of the vertex set X such that the subhypergraph 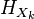 generated by Xk is transitive for each
generated by Xk is transitive for each  , and such that
, and such that
where r(H) is the rank of H.
As a corollary, an edge-transitive hypergraph that is not vertex-transitive is bicolorable.
Graph partitioning (and in particular, hypergraph partitioning) has many applications to IC design.[2]
[edit] Theorems
Many theorems and concepts involving graphs also hold for hypergraphs. Ramsey's theorem and Line graph of a hypergraph are typical examples. Some methods for studying symmetries of graphs extend to hypergraphs.
Two prominent theorems are the Erdős–Ko–Rado theorem and the Kruskal–Katona theorem on uniform hypergraphs.
[edit] Generalizations
One possible generalization of a hypergraph is to allow edges to point at other edges. There are two variations of this generalization. In one, the edges consist not only of a set of vertices, but may also contain subsets of vertices, ad infinitum. Set membership then provides an ordering, but the ordering is neither a partial order nor a preorder, since it is not transitive. The graph corresponding to the Levi graph of this generalization is a directed acyclic graph. Consider, for example, the generalized hypergraph whose vertex set is V = {a,b} and whose edges are e1 = {a,b} and e2 = {a,e1}. Then, although 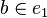 and
and 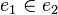 , it is not true that
, it is not true that 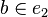 . However, the transitive closure of set membership for such hypergraphs does induce a partial order, and "flattens" the hypergraph into a partially ordered set.
. However, the transitive closure of set membership for such hypergraphs does induce a partial order, and "flattens" the hypergraph into a partially ordered set.
Alternately, edges can be allowed to point at other edges, (irrespective of the requirement that the edges be ordered as directed, acyclic graphs). This allows graphs with edge-loops, which need not contain vertices at all. For example, consider the generalized hypergraph consisting of two edges e1 and e2, and zero vertices, so that e1 = {e2} and e2 = {e1}. As this loop is infinitely recursive, sets that are the edges violate the axiom of foundation. In particular, there is no transitive closure of set membership for such hypergraphs. Although such structures may seem strange at first, they can be readily understood by noting that the equivalent generalization of their Levi graph is no longer bipartite, but is rather just some general directed graph.
The generalized incidence matrix for such hypergraphs is, by definition, a square matrix, of a rank equal to the total number of vertices plus edges. Thus, for the above example, the incidence matrix is simply
[edit] See also
[edit] Notes
- ^ E. Dauber, in Graph theory, ed. F. Harary, Addison Wesley, (1969) p. 172.
- ^ Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (March 1999). "Multilevel hypergraph partitioning: applications in VLSI domain". IEEE Transactions on Very Large Scale Integration (VLSI) Systems 7 (1): pp. 69–79. doi:. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=748202.
[edit] References
- Claude Berge, Dijen Ray-Chaudhuri, "Hypergraph Seminar, Ohio State University 1972", Lecture Notes in Mathematics 411 Springer-Verlag
- This article incorporates material from hypergraph on PlanetMath, which is licensed under the GFDL.


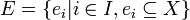

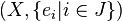

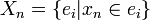
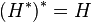

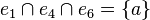


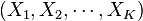

![\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \right].](http://upload.wikimedia.org/math/7/e/c/7ec3b44ef015d86b3ff22ab7bc9342fa.png)

