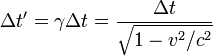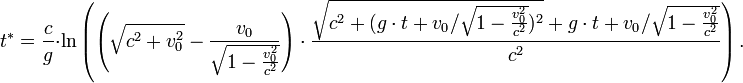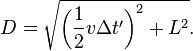appcwiki article astronomy cc_post chronox ciência dilation einstein encyclopedia generalrelativity gr gtd math needs physics readingstuff referenceinformation relativity science space space_flight time time-dilation timedilation work

My tags:

From Wikipedia, the free encyclopedia

This article needs additional citations for verification. Please help improve this article by adding reliable references (ideally, using inline citations). Unsourced material may be challenged and removed. (May 2008)

Contents 1 Overview 2 Experimental confirmation 2.1 Velocity time dilation tests 2.2 Gravitational time dilation tests 2.3 Velocity and gravitational time dilation combined-effect tests 2.4 Meson lifetime 3 Time dilation and space flight 3.1 Time dilation at constant acceleration 4 Simple inference of time dilation 5 Time dilation is symmetric between two inertial observers 5.1 Temporal coordinate systems and clock synchronization 5.2 The spacetime geometry of velocity time dilation 6 See also 7 References 8 External links 8.1 tags

This article discusses a concept in physics. For the concept in sociology, see time displacement.

Time dilation is the phenomenon whereby an observer finds that another's clock, which is physically identical to their own, is ticking at a slower rate as measured by their own clock. This is often interpreted as time "slowing down" for the other clock, but that is only true in the context of the observer's frame of reference. Locally (i.e., from the perspective of any observer within the same frame of reference, without reference to another frame of reference), time always passes at the same rate. The time dilation phenomenon applies to any process that manifests change over time.

In Albert Einstein's theories of relativity, time dilation is manifested in two circumstances:

• In special relativity, clocks that are moving with respect to an inertial system of observation are measured to be running slower. This effect is described precisely by the Lorentz transformation.

• In general relativity, clocks at lower potentials in a gravitational field — such as in proximity to a planet — are found to be running slower. This gravitational time dilation is only briefly mentioned in this article; see that article (and also gravitational red shift) for a more detailed discussion.

In special relativity, the time dilation effect is reciprocal: as observed from the point of view of any two clocks which are in motion with respect to each other, it will be the other party's clock that is time dilated. (This presumes that the relative motion of both parties is uniform; that is, they do not accelerate with respect to one another during the course of the observations.)

In contrast, gravitational time dilation (as treated in general relativity) is not reciprocal: an observer at the top of a tower will observe that clocks at ground level tick slower, and observers on the ground will agree. Thus gravitational time dilation is agreed upon by all observers, independent of their altitude.

[edit] Overview

The formula for determining time dilation in special relativity is:

where

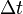is the time interval between two colocal events (i.e. happening at the same place) for an observer in some inertial frame (e.g. ticks on his clock) – this is known as the proper time,

is the time interval between those same events, as measured by another observer, inertially moving with velocity v with respect to the former observer,

is the relative velocity between the observer and the moving clock,

is the speed of light, and

is the Lorentz factor.

Thus the duration of the clock cycle of a moving clock is found to be increased: it is measured to be "running slow". The range of such variances in ordinary life, where v / c < < 1, even considering space travel, are not great enough to produce easily detectable time dilation effects, and such vanishingly small effects can be safely ignored. It is only when an object approaches speeds on the order of 30,000 km/s (1/10 the speed of light) that time dilation becomes important.

Time dilation by the Lorentz factor was predicted by Joseph Larmor (1897), at least for electrons orbiting a nucleus. Thus "... individual electrons describe corresponding parts of their orbits in times shorter for the [rest] system in the ratio :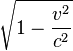" (Larmor 1897). Time dilation of magnitude corresponding to this (Lorentz) factor has been experimentally confirmed, as described below.

[edit] Experimental confirmation

Time dilation has been tested a number of times. The routine work carried on in particle accelerators since the 1950s, such as those at CERN, is a continuously running test of the time dilation of special relativity. The specific experiments include:

[edit] Velocity time dilation tests

• Ives and Stilwell (1938, 1941), “An experimental study of the rate of a moving clock”, in two parts. The stated purpose of these experiments was to verify the time dilation effect, predicted by Lamor-Lorentz ether theory, due to motion through the ether using Einstein's suggestion that Doppler effect in canal rays would provide a suitable experiment. These experiments measured the Doppler shift of the radiation emitted from cathode rays, when viewed from directly in front and from directly behind. The high and low frequencies detected were not the classical values predicted.

and = and

i.e. for sources with invariant frequencies The high and low frequencies of the radiation from the moving sources were measured as

and

as deduced by Einstein (1905) from the Lorentz transformation, when the source is running slow by the Lorentz factor.

• Rossi and Hall (1941) compared the population of cosmic-ray-produced muons at the top of a mountain to that observed at sea level. Although the travel time for the muons from the top of the mountain to the base is several muon half-lives, the muon sample at the base was only moderately reduced. This is explained by the time dilation attributed to their high speed relative to the experimenters. That is to say, the muons were decaying about 10 times slower than if they were at rest with respect to the experimenters.

• Hasselkamp, Mondry, and Scharmann^[1] (1979) measured the Doppler shift from a source moving at right angles to the line of sight (the transverse Doppler shift). The most general relationship between frequencies of the radiation from the moving sources is given by:

as deduced by Einstein (1905)[1]. For () this reduces to f_detected = f_restγ. Thus there is no transverse Doppler shift, and the lower frequency of the moving source can be attributed to the time dilation effect alone.

[edit] Gravitational time dilation tests

• Pound, Rebka in 1959 measured the very slight gravitational red shift in the frequency of light emitted at a lower height, where Earth's gravitational field is relatively more intense. The results were within 10% of the predictions of general relativity. Later Pound and Snider (in 1964) derived an even closer result of 1%. This effect is as predicted by gravitational time dilation.

[edit] Velocity and gravitational time dilation combined-effect tests

• Hafele and Keating, in 1971, flew caesium atomic clocks east and west around the Earth in commercial airliners, to compare the elapsed time against that of a clock that remained at the US Naval Observatory. Two opposite effects came into play. The clocks were expected to age more quickly (show a larger elapsed time) than the reference clock, since they were in a higher (weaker) gravitational potential for most of the trip (c.f. Pound, Rebka). But also, contrastingly, the moving clocks were expected to age more slowly because of the speed of their travel. The gravitational effect was the larger, and the clocks suffered a net gain in elapsed time. To within experimental error, the net gain was consistent with the difference between the predicted gravitational gain and the predicted velocity time loss. In 2005, the National Physical Laboratory in the United Kingdom reported their limited replication of this experiment.^[2] The NPL experiment differed from the original in that the caesium clocks were sent on a shorter trip (London–Washington D.C. return), but the clocks were more accurate. The reported results are within 4% of the predictions of relativity.

• The Global Positioning System can be considered a continuously operating experiment in both special and general relativity. The in-orbit clocks are corrected for both special and general relativistic time dilation effects so that they run at the same rate as clocks on the surface of the Earth. In addition, but not directly time dilation related, general relativistic correction terms are built into the model of motion that the satellites broadcast to receivers — uncorrected, these effects would result in an approximately 7-metre (23 ft) oscillation in the pseudo-ranges measured by a receiver over a cycle of 12 hours.

[edit] Meson lifetime

A comparison of μ-meson lifetimes at different speeds is possible. In the laboratory, slow mesons are produced, and in the atmosphere very fast moving mesons are introduced by cosmic rays. Taking the meson lifetime at rest as the laboratory value of 2.22 μs, the lifetime of a cosmic ray produced meson traveling at 98% of the speed of light is about five times longer, in agreement with observations.^[3] In this experiment the "clock" is the time taken by processes leading to meson decay, and these processes take place in the moving meson at its own "clock rate", which is much slower than the laboratory clock. To explore further, see A compact apparatus for muon lifetime measurement and time dilation demonstration in the undergraduate laboratory and Decay law of moving unstable particle.

[edit] Time dilation and space flight

Time dilation would make it possible for passengers in a fast-moving vehicle to travel further into the future while aging very little, in that their great speed slows down the rate of passage of on-board time. That is, the ship's clock (and according to relativity, any human travelling with it) shows less elapsed time than the clocks of observers on Earth. For sufficiently high speeds the effect is dramatic. For example, one year of travel might correspond to ten years at home. Indeed, a constant 1 g acceleration would permit humans to travel as far as light has been able to travel since the big bang (some 13.7 billion light years) in one human lifetime. The space travellers could return to Earth billions of years in the future. A scenario based on this idea was presented in the novel Planet of the Apes by Pierre Boulle.

A more likely use of this effect would be to enable humans to travel to nearby stars without spending their entire lives aboard the ship. However, any such application of time dilation during Interstellar travel would require the use of some new, advanced method of propulsion.

Current space flight technology has fundamental theoretical limits based on the practical problem that an increasing amount of energy is required for propulsion as a craft approaches the speed of light. The likelihood of collision with small space debris and other particulate material is another practical limitation. At the velocities presently attained, however, time dilation is not a factor in space travel. Travel to regions of space-time where gravitational time dilation is taking place, such as within the gravitational field of a black hole but outside the event horizon (perhaps on a hyperbolic trajectory exiting the field), could also yield results consistent with present theory.

[edit] Time dilation at constant acceleration

In special relativity, time dilation is most simply described in circumstances where relative velocity is unchanging. Nevertheless, the Lorentz equations allow one to calculate proper time and movement in space for the simple case of a spaceship whose acceleration, relative to some referent object in uniform (i.e. constant velocity) motion, equals g throughout the period of measurement.

Let t be the time in an inertial frame subsequently called the rest frame. Let x be a spatial coordinate, and let the direction of the constant acceleration as well as the spaceship's velocity (relative to the rest frame) be parallel to the x-axis. Assuming the spaceship's position at time t = 0 being x = 0 and the velocity being v₀, the following formulas hold [2]:

Position:

Velocity:

Proper time:

Time in the rest frame as a function of x:

[edit] Simple inference of time dilation

Time dilation can be inferred from the constancy of the speed of light in all reference frames as follows:

Consider a simple clock consisting of two mirrors A and B, between which a light pulse is bouncing. The separation of the mirrors is L, and the clock ticks once each time it hits a given mirror.

In the frame where the clock is at rest (diagram at right), the light pulse traces out a path of length 2L and the period of the clock is 2L divided by the speed of light:

From the frame of reference of a moving observer traveling at the speed v (diagram at lower right), the light pulse traces out a longer, angled path. The second postulate of special relativity states that the speed of light is constant in all frames, which implies a lengthening of the period of this clock from the moving observer's perspective. That is to say, in a frame moving relative to the clock, the clock appears to be running more slowly. Straightforward application of the Pythagorean theorem leads to the well-known prediction of special relativity:

The total time for the light pulse to trace its path is given by

The length of the half path can be calculated as a function of known quantities as

Substituting D from this equation into the previous, and solving for Δt' gives:

and thus, with the definition of Δt:

which expresses the fact that for the moving observer the period of the clock is longer than in the frame of the clock itself.

[edit] Time dilation is symmetric between two inertial observers

Common sense would dictate that if time passage has slowed for a moving object, the moving object would observe the external world to be correspondingly "sped up". Counterintuitively, special relativity predicts the opposite.

A similar oddity occurs in everyday life. If Sam sees Abigail at a distance she appears small to him and at the same time Sam appears small to Abigail. Experience has taught us to accept the quirks of perspective but left us unprepared for relativity.

We are accustomed to the notion of relativity with respect to distance: the distance from Los Angeles to New York is by convention the same as the distance from New York to Los Angeles. On the other hand, when we consider speeds, we think of an object as "actually" moving, overlooking that its motion is always relative to something else — to the stars, the ground or to oneself. If one object is moving with respect to another, the latter is moving with respect to the former and with equal relative speed.

In the special theory of relativity, a moving clock is found to be ticking slowly with respect to the observer's clock. If Sam and Abigail are on different trains in near-lightspeed relative motion, Sam measures (by all methods of measurement) clocks on Abigail's train to be running slowly and, similarly, Abigail measures clocks on Sam's train to be running slowly.

Note that in all such attempts to establish "synchronization" within the reference system, the question of whether something happening at one location is in fact happening simultaneously with something happening elsewhere is of key importance. Calculations are ultimately based on determining which events are simultaneous. Notice also that establishing simultaneity of events separated in space necessarily requires transmission of information between locations, which by itself is an indication that the speed of light will enter the determination of simultaneity.

It is a natural and legitimate question to ask how, in detail, special relativity can be self-consistent if clock A is time-dilated with respect to clock B and clock B is also time-dilated with respect to clock A. It is by challenging the assumptions we build into the common notion of simultaneity that logical consistency can be restored. Simultaneity is a relationship between an observer in a particular frame of reference and a set of events. By analogy, we accept that left and right vary with the position of the observer. That is because left and right apply to a relationship. In a similar vein, Plato explained to the confused that up and down describe a relationship to the earth and one would not fall off at the antipodes.

Within the framework of the theory and its terminology there is a relativity of simultaneity that affects how the specified events are aligned with respect to each other by observers who are in relative motion. Because the pairs of putatively simultaneous moments are identified differently by different observers (as illustrated in the twin paradox article), each can treat the other clock as being the slow one without relativity being self-contradictory. For those seeking a more explicit account, this can be explained in many ways, some of which follow.

[edit] Temporal coordinate systems and clock synchronization

In Relativity, temporal coordinate systems are set up using a procedure for synchronizing clocks, discussed by Poincaré (1900) in relation to Lorentz's local time (see relativity of simultaneity). It is now usually called the Einstein synchronization procedure, since it appeared in his 1905 paper.

An observer with a clock sends a light signal out at time t₁ according to his clock. At a distant event, that light signal is reflected back to, and arrives back to the observer at time t₂ according to his clock. Since the light travels the same path at the same rate going both out and back for the observer in this scenario, the coordinate time of the event of the light signal being reflected for the observer t_E is t_E = (t₁ + t₂) / 2. In this way, a single observer's clock can be used to define temporal coordinates which are good anywhere in the universe.

Symmetric time dilation occurs with respect to temporal coordinate systems set up in this manner. It is an effect where another clock is being viewed as running slowly by an observer. Observers do not consider their own clock time to be time-dilated, but may find that it is observed to be time-dilated in another coordinate system.

[edit] The spacetime geometry of velocity time dilation

The green dots and red dots in the animation represent spaceships. The ships of the green fleet have no velocity relative to each other, so for the clocks onboard the individual ships the same amount of time elapses relative to each other, and they can set up a procedure to maintain a synchronized standard fleet time. The ships of the "red fleet" are moving with a velocity of 0.866 of the speed of light with respect to the green fleet.

The blue dots represent pulses of light. One cycle of light-pulses between two green ships takes two seconds of "green time", one second for each leg.

As seen from the perspective of the reds, the transit time of the light pulses they exchange among each other is one second of "red time" for each leg. As seen from the perspective of the greens, the red ships' cycle of exchanging light pulses travels a diagonal path that is two light-seconds long. (As seen from the green perspective the reds travel 1.73 (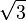) light-seconds of distance for every two seconds of green time.)

One of the red ships emits a light pulse towards the greens every second of red time. These pulses are received by ships of the green fleet with two-second intervals as measured in green time. Not shown in the animation is that all aspects of physics are proportionally involved. The lightpulses that are emitted by the reds at a particular frequency as measured in red time are received at a lower frequency as measured by the detectors of the green fleet that measure against green time, and vice versa.

The animation cycles between the green perspective and the red perspective, to emphasize the symmetry. As there is no such thing as absolute motion in relativity (as is also the case for Newtonian mechanics), both the green and the red fleet are entitled to consider themselves motionless in their own frame of reference.

Again, it is vital to understand that the results of these interactions and calculations reflect the real state of the ships as it emerges from their situation of relative motion. It is not a mere quirk of the method of measurement or communication.

[edit] See also

[edit] References

1. ^ http://www.springerlink.com/content/kt5505r2p2r22411/
2. ^ http://www.npl.co.uk/upload/pdf/metromnia_issue18.pdf
3. ^ JV Stewart (2001). Intermediate electromagnetic theory. Singapore: World Scientific. p. 705. ISBN 9810244703. http://books.google.com/books?id=mwLI4nQ0thQC&pg=PA705&dq=relativity+%22meson+lifetime%22&lr=&as_brr=0&sig=K7KuQfEclGar6TcXC0qQelZJnbI. 

Wikibooks has a book on the topic of Special relativity

• Callender, Craig & Edney, Ralph (2001). Introducing Time. Icon. ISBN 1-84046-592-1. 
• Einstein, A. (1905) "Zur Elektrodynamik bewegter Körper", Annalen der Physik, 17, 891. English translation: On the electrodynamics of moving bodies
• Einstein, A. (1907) "Über eine Möglichkeit einer Prüfung des Relativitätsprinzips", Annalen der Physik.
• Hasselkamp, D., Mondry, E. and Scharmann, A. (1979) "Direct Observation of the Transversal Doppler-Shift", Z. Physik A 289, 151–155
• Ives, H. E. and Stilwell, G. R. (1938), “An experimental study of the rate of a moving clock”, J. Opt. Soc. Am, 28, 215–226
• Ives, H. E. and Stilwell, G. R. (1941), “An experimental study of the rate of a moving clock. II”, J. Opt. Soc. Am, 31, 369–374
• Joos, G. (1959) Lehrbuch der Theoretischen Physik, 11. Auflage, Leipzig; Zweites Buch, Sechstes Kapitel, § 4: Bewegte Bezugssysteme in der Akustik. Der Doppler-Effekt.
• Larmor, J. (1897) "On a dynamical theory of the electric and luminiferous medium", Phil. Trans. Roy. Soc. 190, 205–300 (third and last in a series of papers with the same name).
• Poincaré, H. (1900) "La theorie de Lorentz et la Principe de Reaction", Archives Neerlandaies, V, 253–78.
• Rossi, B and Hall, D. B. Phys. Rev., 59, 223 (1941).
• NIST Two way time transfer for satellites
• Voigt, W. "Ueber das Doppler'sche princip" Nachrichten von der Königlicher Gesellschaft der Wissenschaften zu Göttingen, 2, 41–51.
• REINHARDT et al. Test of relativistic time dilation with fast optical atomic clocks at different velocities (Nature 2007)

[edit] External links

• Time Dilation Demonstration Applet
• UK National Physical Laboratory reports replication of Hefele-Keating experiment

v • d • e Time Major concepts Time · Eternity · Arguments for eternity · Immortality Deep time · History · Past · Present · Future · Futurology Time Portal Measurement and Standards Chronometry · UTC · UT · TAI · Second · Minute · Hour · Sidereal time · Solar time · Time zone Clock · Horology · History of timekeeping devices · Astrarium · Marine chronometer · Sundial · Water clock Calendar · Day · Week · Month · Year · Tropical year · Julian · Gregorian · Islamic   Intercalation · Leap second · Leap year Chronology Astronomical chronology · Geologic Time · Geological history · Geochronology · Archaeological dating Calendar era · Regnal year · Chronicle · Timeline · Periodization Religion and Mythology Time and fate deities · Wheel of time · Kāla · Kalachakra · Prophecy · Dreamtime Philosophy Causality · Eternalism · Eternal return · Event · The Unreality of Time · A-series and B-series · B-Theory of time Endurantism · Four dimensionalism · Perdurantism · Presentism · Temporal finitism · Temporal parts Physical Sciences Time in physics · Spacetime · Absolute time and space · T-symmetry Arrow of time · Chronon · Fourth dimension · Planck epoch · Planck time · Time domain Theory of relativity · Time dilation · Gravitational time dilation · Coordinate time · Proper time Biology Chronobiology · Circadian rhythms Psychology Consciousness and spacetime · Mental chronometry · Reaction time · Sense of time · Specious present Sociology and Anthropology Futures studies · Long Now Foundation · Time discipline · Time use research Economics Newtonian time in economics · Time value of money · Time Banking · Time-based currency Related topics Space · Duration · Time capsule · Time travel · Time signature · System time · Metric time · Hexadecimal time · Carpe diem · Tempus fugit

v • d • e Time measurement and standards Major subjects Time · Chronometry · Orders of magnitude · Units of time · Metrology Time Portal International standards UTC · UT · TAI · ISO 31-1 · Second · DUT1 · Leap second · IERS Terrestrial Time · Geocentric Coordinate Time · Barycentric Coordinate Time Civil time · Minute · Hour · 12-hour clock · 24-hour clock · ISO 8601 International Date Line · Solar time · Time zone · Daylight saving time · Time offset Obsolete standards Ephemeris time · Barycentric Dynamical Time · Greenwich Mean Time · Prime Meridian Time in physics Spacetime · Chronon · Cosmological decade · Planck epoch · Planck time · T-symmetry Theory of relativity · Time dilation · Gravitational time dilation · Coordinate time · Proper time Time domain · Continuous time · Discrete time · Absolute time and space Horology Clock · Astrarium · Atomic clock · Hourglass · Marine chronometer · Radio clock · Sundial · Watch · Water clock History of timekeeping devices · Equation of time · Complication Calendar Day · Week · Month · Year · Decade · Century · Millennium Astronomical · Julian · Gregorian · Islamic · Lunisolar · Solar · Lunar · Epact · Intercalation · Leap year Tropical year · Equinox · Solstice · Seven-day week · Week-day names · Calculating the day of the week · Dominical letter Archaeology & geology International Commission on Stratigraphy · Geologic Time · Archaeological dating Astronomical chronology Nuclear time scale · Precession · Sidereal time · Galactic year Unusual units Fortnight · Jiffy · Lustrum · Saeculum · Shake · Tide Related topics Chronology · Duration · System time · Metric time · Mental chronometry · Time value of money · Timekeeper

[edit] tags

This article needs additional citations for verification. Please help improve this article by adding reliable references (ideally, using inline citations). Unsourced material may be challenged and removed. (May 2008)