Topological sorting
From Wikipedia, the free encyclopedia
In graph theory, a topological sort or topological ordering of a directed acyclic graph (DAG) is a linear ordering of its nodes in which each node comes before all nodes to which it has outbound edges. Every DAG has one or more topological sorts.
More formally, define the partial order relation R over the nodes of the DAG such that xRy if and only if there is a directed path from x to y. Then, a topological sort is a linear extension of this partial order, that is, a total order compatible with the partial order.
Contents |
[edit] Examples
The canonical application of topological sorting (topological order) is in scheduling a sequence of jobs or tasks; topological sorting algorithms were first studied in the early 1960s in the context of the PERT technique for scheduling in project management (Jarnagin 1960). The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started (for example, when washing clothes, the washing machine must finish before we put the clothes to dry). Then, a topological sort gives an order in which to perform the jobs.
In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluation when recomputing formula values in spreadsheets, logic synthesis, determining the order of compilation tasks to perform in makefiles, and resolving symbol dependencies in linkers.
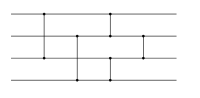
The graph shown to the left has many valid topological sorts, including:
|
[edit] Algorithms
The usual algorithms for topological sorting have running time linear in the number of nodes plus the number of edges (O(|V|+|E|)).
One of these algorithms, first described by Kahn (1962), works by choosing vertices in the same order as the eventual topological sort. First, find a list of "start nodes" which have no incoming edges and insert them into a set S; at least one such node must exist if graph is acyclic. Then:
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
insert n into L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
output error message (graph has at least one cycle)
else
output message (proposed topologically sorted order: L)
If the graph was a DAG, a solution is contained in the list L (the solution is not unique). Otherwise, the graph has at least one cycle and therefore a topological sorting is impossible.
Note that, reflecting the non-uniqueness of the resulting sort, the structure S can be simply a set or a queue or a stack. Depending on the order that nodes n are removed from set S, a different solution is created.
An alternative algorithm for topological sorting is based on depth-first search. Loop through the vertices of the graph, in any order, initiating a depth-first search for any vertex that has not already been visited by a previous search. The desired topological sorting is the reverse postorder of these searches. That is, we can construct the ordering as a list of vertices, by adding each vertex to the start of the list at the time when the depth-first search is processing that vertex and has returned from processing all children of that vertex. Since each edge and vertex is visited once, the algorithm runs in linear time. This depth-first search based algorithm is the one described by Cormen, Leiserson & Rivest (1990); it seems to have been first described in print by Tarjan (1976).
[edit] Uniqueness
If a topological sort has the property that all pairs of consecutive vertices in the sorted order are connected by edges, then these edges form a directed Hamiltonian path in the DAG. If a Hamiltonian path exists, the topological sort order is unique; no other order respects the edges of the path. Conversely, if a topological sort does not form a Hamiltonian path, the DAG will have two or more valid topological orderings, for in this case it is always possible to form a second valid ordering by swapping two consecutive vertices that are not connected by an edge to each other. Therefore, it is possible to test in polynomial time whether a unique ordering exists, and whether a Hamiltonian path exists, despite the NP-hardness of the Hamiltonian path problem for more general directed graphs (Vernet & Markenzon 1997).
[edit] References
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms. MIT Press and McGraw-Hill. First Edition, 1990, ISBN 0-07-013143-0, Section 23.4: Topological sort, pp.485–488; Second Edition, 2001, ISBN 0-262-03293-7, Section 22.4: Topological sort, pp.549–552.
- Jarnagin, M. P. (1960), Automatic machine methods of testing PERT networks for consistency, Technical Memorandum No. K-24/60, Dahlgren, Virginia: U. S. Naval Weapons Laboratory.
- Kahn, A. B. (1962), "Topological sorting of large networks", Communications of the ACM 5 (11): 558–562, doi:.
- Tarjan, Robert E. (1976), "Edge-disjoint spanning trees and depth-first search", Algorithmica 6 (2): 171–185, doi:.
- Vernet, Lilian; Markenzon (1997), "Hamiltonian problems for reducible flowgraphs", Proc. 17th International Conference of the Chilean Computer Science Society (SCCC '97), pp. 264–267, doi:.
[edit] See also
- tsort, a Unix program for topological sorting
- make (software), a Unix program for build automation
- Feedback arc set, a (possibly empty) set of arcs which, if removed from the graph, make it possible to topologically sort it. Useful for dealing with graphs with cycles.
[edit] External links
- NIST Dictionary of Algorithms and Data Structures: topological sort
- Eric W. Weisstein, TopologicalSort at MathWorld.
|
||||||||||||||||||||||||||||