Standard score

From Wikipedia, the free encyclopedia

comparison of various measures of the normal distribution: standard deviations, cumulative percentages, Z-scores, and T-scores

"Standardize" redirects here. For industrial and technical standards, see Standardization.

For Z-values in ecology, see Z-value.

For Z-factor in high-throughput screening, see Z-factor.

In statistics, a standard score is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation. This conversion process is called standardizing or normalizing; however, "normalizing" can refer to many types of ratios; see normalization (statistics) for more.

Standard scores are also called z-values, z-scores, normal scores, and standardized variables.

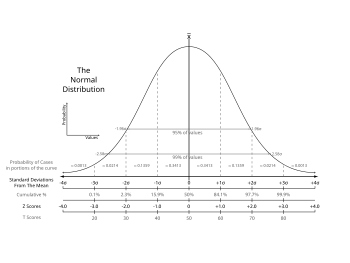
The standard score indicates how many standard deviations an observation is above or below the mean. It allows comparison of observations from different normal distributions, which is done frequently in research.

The standard score is not the same as the z-factor used in the analysis of high-throughput screening data, but is sometimes confused with it.

The standard deviation is the unit of measurement of the z-score.

[edit] Formula

The standard score is

$z = \frac{x - \mu}{\sigma},$

where:

x is a raw score to be standardized;

μ is the mean of the population;

σ is the standard deviation of the population.

The quantity z represents the distance between the raw score and the population mean in units of the standard deviation. z is negative when the raw score is below the mean, positive when above.

A key point is that calculating z requires the population mean and the population standard deviation, not the sample mean or sample deviation. It requires knowing the population parameters, not the statistics of a sample drawn from the population of interest. But knowing the true standard deviation of a population is often unrealistic except in cases such as standardized testing, where the entire population is measured. In cases where it is impossible to measure every member of a population, the standard deviation may be estimated using a random sample. For example, a population of people who smoke cigarettes is not fully measured.

If using sample mean and sample deviation, one should instead use studentized residuals, as there is the added complication that variations of residuals do not in general equal variations of errors.

When a population is normally distributed, the percentile rank may be determined from the standard score and statistical tables.