Poisson process
From Wikipedia, the free encyclopedia
A Poisson process, named after the French mathematician Siméon-Denis Poisson (1781 – 1840), is the stochastic process in which events occur continuously and independently of one another (the word event used here is not an instance of the concept of event frequently used in probability theory). A well-known example is radioactive decay of atoms. Many processes are not exactly Poisson processes, but similar enough that for certain types of analysis they can be regarded as such; e.g., telephone calls arriving at a switchboard (if we assume that their frequency doesn't vary with the time of day), page view requests to a website, rainfall or radioactive decay.
The Poisson process is a collection  of random variables, where N(t) is the number of events that have occurred up to time t (starting from time 0). The number of events between time a and time b is given as N(b) − N(a) and has a Poisson distribution. Each realization of the process {N(t)} is a non-negative integer-valued step function that is non-decreasing, but for intuitive purposes it is usually easier to think of it as a point pattern on [0,∞) (the points in time where the step function jumps, i.e. the points in time where an event occurs).
of random variables, where N(t) is the number of events that have occurred up to time t (starting from time 0). The number of events between time a and time b is given as N(b) − N(a) and has a Poisson distribution. Each realization of the process {N(t)} is a non-negative integer-valued step function that is non-decreasing, but for intuitive purposes it is usually easier to think of it as a point pattern on [0,∞) (the points in time where the step function jumps, i.e. the points in time where an event occurs).
The Poisson process is a continuous-time process: its discrete-time counterpart is the Bernoulli process. The Poisson process is one of the most well-known Lévy processes. Poisson processes are also examples of continuous-time Markov processes. A Poisson process is a pure-birth process, the simplest example of a birth-death process. By the aforementioned interpretation as a random point pattern on [0,∞) it is also a point process on the real half-line.
Contents |
[edit] Definition
A Poisson process is a continuous-time counting process {N(t), t ≥ 0} that possesses the following properties:
- N(0) = 0
- Independent increments (the numbers of occurrences counted in disjoint intervals are independent from each other)
- Stationary increments (the probability distribution of the number of occurrences counted in any time interval only depends on the length of the interval)
- No counted occurrences are simultaneous.
[edit] Types of Poisson processes
[edit] Homogeneous Poisson process
A homogeneous Poisson process is characterized by a rate parameter λ, also known as intensity, such that the number of events in time interval (t,t + τ] follows a Poisson distribution with associated parameter λτ. This relation is given as
where N(t + τ) − N(t) describes the number of events in time interval (t,t + τ].
Just as a Poisson random variable is characterized by its scalar parameter λ, a homogeneous Poisson process is characterized by its rate parameter λ, which is the expected number of "events" or "arrivals" that occur per unit time.
N(t) is a sample homogeneous Poisson process, not to be confused with a density or distribution function.
[edit] Non-homogeneous Poisson process
(also known as an inhomogeneous Poisson process)
In general, the rate parameter may change over time. In this case, the generalized rate function is given as λ(t). Now the expected number of events between time a and time b is
Thus, the number of arrivals in the time interval (a, b], given as N(b) − N(a), follows a Poisson distribution with associated parameter λa,b
A homogeneous Poisson process may be viewed as a special case when λ(t) = λ, a constant rate.
[edit] Spatial Poisson process
A further variation on the Poisson process, called the spatial Poisson process, introduces a spatial dependence on the rate function and is given as  where
where  for some vector space V (e.g. R2 or R3). For any set
for some vector space V (e.g. R2 or R3). For any set 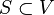 (e.g. a spatial region) with finite measure, the number of events occurring inside this region can be modelled as a Poisson process with associated rate function λS(t) such that
(e.g. a spatial region) with finite measure, the number of events occurring inside this region can be modelled as a Poisson process with associated rate function λS(t) such that
In the special case that this generalized rate function is a separable function of time and space, we have:
for some function 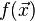 . Without loss of generality, let
. Without loss of generality, let
(If this is not the case, λ(t) can be scaled appropriately.) Now, 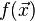 represents the spatial probability density function of these random events in the following sense. The act of sampling this spatial Poisson process is equivalent to sampling a Poisson process with rate function λ(t), and associating with each event a random vector
represents the spatial probability density function of these random events in the following sense. The act of sampling this spatial Poisson process is equivalent to sampling a Poisson process with rate function λ(t), and associating with each event a random vector  sampled from the probability density function
sampled from the probability density function 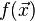 . A similar result can be shown for the general (non-separable) case.
. A similar result can be shown for the general (non-separable) case.
[edit] General characteristics of the Poisson process
In its most general form, the only two conditions for a stochastic process to be a Poisson process are:
- Orderliness: which roughly means
- which implies that arrivals don't occur simultaneously (but this is actually a mathematically stronger statement).
- Memorylessness (also called evolution without after-effects): the number of arrivals occurring in any bounded interval of time after time t is independent of the number of arrivals occurring before time t and the time since the last arrival.
These seemingly unrestrictive conditions actually impose a great deal of structure in the Poisson process. In particular, they imply that the time between consecutive events (called interarrival times) are independent random variables. For the homogeneous Poisson process, these inter-arrival times are exponentially distributed with parameter λ (mean 1 / λ);. Also, the memorylessness property shows that the number of events in one time interval is independent from the number of events in an interval that is disjoint from the first interval. This latter property is known as the independent increments property of the Poisson process.
To illustrate the exponentially-distributed inter-arrival times property, consider a homogeneous Poisson process N(t) with rate parameter λ, and let Tk be the time of the kth arrival, for k = 1, 2, 3, ... . Clearly the number of arrivals before some fixed time t is less than k if and only if the waiting time until the kth arrival is more than t. In symbols, the event [ N(t) < k ] occurs if and only if the event [ Tk > t ] occurs. Consequently the probabilities of these events are the same:
- P(Tk > t) = P(N(t) < k).
In particular, consider the waiting time until the first arrival. Clearly that time is more than t if and only if the number of arrivals before time t is 0. Combining this latter property with the above probability distribution for the number of homogeneous Poisson process events in a fixed interval gives
Consequently, the waiting time until the first arrival T1 has an exponential distribution, and is thus memoryless. One can similarly show that the other interarrival times Tk − Tk − 1 share the same distribution. Hence, they are independent, identically-distributed (i.i.d.) random variables with parameter λ > 0; and expected value 1/λ. For example, if the average rate of arrivals is 5 per minute, then the average waiting time between arrivals is 1/5 minute.
[edit] Examples
- The long-term behavior of the number of web page requests arriving at a server may be characterized by a Poisson process except for unusual circumstances such as coordinated denial of service attacks or flash crowds. Such a model assumes homogeneity as well as weak stationarity.
- The number of telephone calls arriving at a switchboard, or at an automatic phone-switching system, may be characterized by a Poisson process.
- The number of photons hitting a photodetector.
- The number of particles emitted via radioactive decay by an unstable substance may be characterized by a non-homogeneous Poisson process, where the rate decays as the substance stabilizes.
- The number of raindrops falling over an area may be characterized by a spatial Poisson process.
- The arrival of "customers" is commonly modelled as a Poisson process in the study of simple queueing systems.
[edit] See also
- Compound Poisson distribution
- Compound Poisson process
- Continuous-time Markov process
- Cox process (generalization)
- Gamma distribution
- Markovian arrival processes
- Poisson sampling
[edit] Further reading
- Cox, D.R., Isham, V.I. (1980) Point Processes. Chapman & Hall. ISBN 0-412-21910-7.
- Snyder, D.L., Miller, M.I. (1991) Random Point Processes in Time and Space. Springer-Verlag. ISBN 0-387-97577-2.
- Ross, S.M. (1995) Stochastic Processes. Wiley. ISBN 978-0471120629

![P [(N(t+ \tau) - N(t)) = k] = \frac{e^{-\lambda \tau} (\lambda \tau)^k}{k!} \qquad k= 0,1,\ldots,](http://upload.wikimedia.org/math/7/2/8/7286a85d115010d6b56c2bddb8ec4356.png)

![P [(N(b) - N(a)) = k] = \frac{e^{-\lambda_{a,b}} (\lambda_{a,b})^k}{k!} \qquad k= 0,1,\ldots.](http://upload.wikimedia.org/math/9/b/2/9b2337e27ab46daee47ba57b203674a6.png)


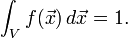

![P(T_1>t)=P(N(t)=0)=P [(N(t) - N(0)) = 0] = \frac{e^{-\lambda t} (\lambda t)^0}{0!} = e^{-\lambda t}.](http://upload.wikimedia.org/math/d/c/5/dc587b01a0decead27fca33adcd4d27b.png)

