Constraint satisfaction problem

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Constraint satisfaction problems or CSPs are mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint satisfaction methods. CSPs are the subject of intense research in both artificial intelligence and operations research, since the regularity in their formulation provides a common basis to analyze and solve problems of many unrelated families. CSPs often exhibit high complexity, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time.

Examples of problems that can be modeled as a constraint satisfaction problem:

Contents

[edit] Formal definition

Formally, a constraint satisfaction problem is defined as a triple \langle X,D,C \rangle, where X is a set of variables, D is a domain of values, and C is a set of constraints. Every constraint is in turn a pair \langle t,R \rangle, where t is a tuple of variables and R is a set of tuples of values; all these tuples having the same number of elements; as a result R is a relation. 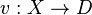An evaluation of the variables is a function from variables to domains, v:X \rightarrow D. Such an evaluation satisfies a constraint \langle (x_1,\ldots,x_n),R \rangle if (v(x_1),\ldots,v(x_n)) \in R. A solution is an evaluation that satisfies all constraints.

[edit] Resolution of CSPs

Constraint satisfaction problems on finite domains are typically solved using a form of search. The most used techniques are variants of backtracking, constraint propagation, and local search.

Backtracking is a recursive algorithm. It maintains a partial assignment of the variables. Initially, all variables are unassigned. At each step, a variable is chosen, and all possible values are assigned to it in turn. For each value, the consistency of the partial assignment with the constraints is checked; in case of consistency, a recursive call is performed. When all values have been tried, the algorithm backtracks. In this basic backtracking algorithm, consistency is defined as the satisfaction of all constraints whose variables are all assigned. Several variants of backtracking exists. Backmarking improves the efficiency of checking consistency. Backjumping allows saving part of the search by backtracking "more than one variable" in some cases. Constraint learning infers and saves new constraints that can be later used to avoid part of the search. Look-ahead is also often used in backtracking to attempt to foresee the effects of choosing a variable or a value, thus sometimes determining in advance when a subproblem is satisfiable or unsatisfiable.

Constraint propagation techniques are methods used to modify a constraint satisfaction problem. More precisely, they are methods that enforce a form of local consistency, which are conditions related to the consistency of a group of variables and/or constraints. Constraints propagation has various uses. First, they turn a problem into one that is equivalent but is usually simpler to solve. Second, they may prove satisfiability or unsatisfiability of problems. This is not guaranteed to happen in general; however, it always happens for some forms of constraint propagation and/or for some certain kinds of problems. The most known and used form of local consistency are arc consistency, hyper-arc consistency, and path consistency. The most popular constraint propagation method is the AC-3 algorithm, which enforces arc consistency.

Local search methods are incomplete satisfiability algorithms. They may find a solution of a problem, but they may fail even if the problem is satisfiable. They work by iteratively improving a complete assignment over the variables. At each step, a small number of variables are changed value, with the overall aim of increasing the number of constraints satisfied by this assignment. The min-conflicts algorithm is a local search algorithm specific for CSPs and based in that principle. In practice, local search appears to work well when these changes are also affected by random choices. Integration of search with local search have been developed, leading to hybrid algorithms.

[edit] Theoretical aspects of CSPs

CSPs are also studied in computational complexity theory and finite model theory. An important question is whether for each set of relations, the set of all CSPs that can be represented using only relations chosen from that set is either in PTIME or otherwise NP-complete (assuming P ≠ NP). If such a dichotomy is true, then CSPs provide one of the largest known subsets of NP which avoids problems that are neither polynomial time solvable nor NP-complete, whose existence was demonstrated by Ladner. Dichotomy results are known for CSPs where the domain of values is of size 2 or 3, but the general case is still open.

Most classes of CSPs that are known to be tractable are those where the hypergraph of constraints has bounded treewidth (and there are no restrictions on the set of constraint relations), or where the constraints have arbitrary form but there exist essentially non-unary polymorphisms[clarification needed] of the set of constraint relations.

[edit] Variants of CSPs

The classic model of Constraint Satisfaction Problem defines a model of static, inflexible constraints. This rigid model is a shortcoming that makes it difficult to represent problems easily [1]. Several modifications of the basic CSP definition have been proposed to adapt the model to a wide variety of problems.

[edit] Dynamic CSPs

Dynamic CSPs[2] (DCSPs) are useful when the original formulation of a problem is altered in some way, typically because the set of constraints to consider evolves because of the environment.[3] DCSPs are viewed as a sequence of static CSPs, each one a transformation of the previous one in which variables and constraints can be added (restriction) or removed (relaxation). Information found in the initial formulations of the problem can be used to refine the next ones. The solving method can be classified according to the way in which information is transferred:

  • Oracles: the solution found to previous CSPs in the sequence are used to as heuristics to guide the resolution of the current CSP from scratch.
  • Local repair: each CSP is calculated starting from the partial solution of the previous one and repairing the inconsistent constraints with local search.
  • Constraint recording: new constraints are defined in each stage of the search to represent the learning of inconsistent group of decisions. Those constraints are carried over the new CSP problems.

[edit] Flexible CSPs

Classic CSPs treat constraints as hard, meaning that they are imperative (each solution must satisfy all them) and inflexible (in the sense that they must be completely satisfied or else they are completely violated). Flexible CSPs relax those assumptions, partially relaxing the constraints and allowing the solution to not comply with all them. Some types of flexible CSPs include:

  • MAX-CSP, where a number of constraints are allowed to be violated, and the quality of a solution is better by how low is that number.
  • Weighted CSP, a MAX-CSP in which each violation of a constraint is weighted according to a predefined preference. Thus satisfying constraint with more weight is preferred.
  • Fuzzy CSP model constraints as fuzzy relations in which the satisfaction of a constraint is a continuous function of its variables' values, going from fully satisfied to fully violated.

[edit] References

  1. ^ Dynamic Flexible Constraint Satisfaction and Its Application to AI Planning, Ian Miguel
  2. ^ Dechter, R. and Dechter, A. Belief. Maintenance in Dynamic Constraint Networks In Proc. of AAAI-88, 37-42. [1]
  3. ^ Solution reuse in dynamic constraint satisfaction problems, Thomas Schiex

[edit] See also

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Constraint_satisfaction_problem"
Personal tools