Economic order quantity

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Corporate finance

Working capital management

Cash conversion cycle
Return on capital
Economic value added
Just In Time
Economic order quantity
Discounts and allowances
Factoring (finance)
Capital budgeting

Capital investment decisions
The investment decision
The financing decision
Sections

Managerial finance
Financial accounting
Management accounting
Mergers and acquisitions
Balance sheet analysis
Business plan
Corporate action
Finance series

Financial market
Financial market participants
Corporate finance
Personal finance
Public finance
Banks and Banking
Financial regulation
This box: view • talk • edit

Economic order quantity is the level of inventory that minimizes the total inventory holding costs and ordering costs. The framework used to determine this order quantity is also known as Wilson EOQ Model. The model was developed by F. W. Harris in 1913. But still R. H. Wilson is given credit for his early in-depth analysis of the model.

Contents

[edit] Underlying assumptions

  1. The ordering cost is constant.
  2. The rate of demand is constant
  3. The lead time is fixed
  4. The purchase price of the item is constant i.e no discount is available
  5. The replenishment is made instantaneously, the whole batch is delivered at once.

EOQ is the quantity to order, so that ordering cost + carrying cost finds its minimum. (Common misunderstanding is, that formula tries to find when these are equal.)

[edit] Variables

  • Q = order quantity
  • Q * = optimal order quantity
  • D = annual demand quantity of the product
  • P = purchase cost per unit
  • C = fixed cost per order (not per unit, in addition to unit cost)
  • H = annual holding cost per unit (also known as carrying cost) (warehouse space, refrigeration, insurance, etc. usually not related to the unit cost)

[edit] The Total Cost function

The single-item EOQ formula finds the minimum point of the following cost function: EOQ is the level of the inventory where ordering cost and carrying cost remains equal.

Total Cost = purchase cost + ordering cost + holding cost

- Purchase cost: This is the variable cost of goods: purchase unit price × annual demand quantity. This is P×D

- Ordering cost: This is the cost of placing orders: each order has a fixed cost C, and we need to order D/Q times per year. This is C × D/Q

- Holding cost: the average quantity in stock (between fully replenished and empty) is Q/2, so this cost is H × Q/2

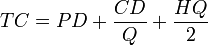TC = PD + {\frac{CD}{Q}} + {\frac{HQ}{2}}.

In order to determine the minimum point of the total cost curve, set its derivative equal to zero:

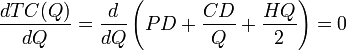{\frac{dTC(Q)}{dQ}} = {\frac{d}{dQ}}\left(PD + {\frac{CD}{Q}} + {\frac{HQ}{2}}\right)=0.

The result of this derivation is:

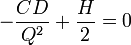-{\frac{CD}{Q^2}} + {\frac{H}{2}}=0.

Solving for Q gives Q* (the optimal order quantity):

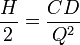
{\frac{H}{2}}={\frac{CD}{Q^2}}

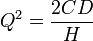
Q^2={\frac{2CD}{H}}

Therefore: Q^* = \sqrt{\frac{2CD}{H}} .

Note that interestingly, Q* is independent of P, it is a function of only C, D, H.

[edit] Extensions

Several extensions can be made to the EOQ model, including backordering costs and multiple items. Additionally, the economic order interval can be determined from the EOQ and the economic production quantity model (which determines the optimal production quantity) can be determined in a similar fashion.

[edit] See also

[edit] References

  • Harris, F.W. "How Many Parts To Make At Once" Factory, The Magazine of Management, 10(2), 135-136, 152 (1913).
  • Harris, F. W. Operations Cost (Factory Management Series), Chicago: Shaw (1915).
  • Wilson, R. H. "A Scientific Routine for Stock Control" Harvard Business Review, 13, 116-128 (1934).

[edit] Links

Retrieved from "http://en.wikipedia.org/wiki/Economic_order_quantity"
Personal tools