Graphene

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Not to be confused with Grapheme.

Graphene is a one-atom-thick planar sheet of sp2-bonded carbon atoms that are densely packed in a honeycomb crystal lattice. It can be viewed as an atomic-scale chicken wire made of carbon atoms and their bonds. The name comes from GRAPHITE + -ENE; graphite itself consists of many graphene sheets stacked together.

The carbon-carbon bond length in graphene is approximately 0.142 nm. Graphene is the basic structural element of some carbon allotropes including graphite, carbon nanotubes and fullerenes. It can also be considered as an infinitely large aromatic molecule, the limiting case of the family of flat polycyclic aromatic hydrocarbons called graphenes.

Graphene is also very strong. It is 200 times stronger than steel, making it the strongest material.

Graphene is an atomic-scale honeycomb lattice made of carbon atoms.
The relation of Graphene to Graphite.
(The blue balls, e.g. intercalated oxygen atoms, must be deleted.)

Contents

[edit] Description

Perfect graphenes consist exclusively of hexagonal cells; pentagonal and heptagonal cells constitute defects. If an isolated pentagonal cell is present, then the plane warps into a cone shape; insertion of 12 pentagons would create a fullerene. Likewise, insertion of an isolated heptagon causes the sheet to become saddle-shaped. Controlled addition of pentagons and heptagons would allow a wide variety of complex shapes to be made, for instance carbon NanoBuds. Single-walled carbon nanotubes may be considered to be graphene cylinders; some have a hemispherical graphene cap (that includes 6 pentagons) at each end.

The IUPAC compendium of technology states: "previously, descriptions such as graphite layers, carbon layers, or carbon sheets have been used for the term graphene…it is not correct to use for a single layer a term which includes the term graphite, which would imply a three-dimensional structure. The term graphene should be used only when the reactions, structural relations or other properties of individual layers are discussed". In this regard, graphene has been referred to as an infinite alternant (only six-member carbon ring) polycyclic aromatic hydrocarbon (PAH). The largest molecule of this type consists of 222 atoms and is 10 benzene rings across.[1] The onset of graphene properties, as compared to those of a PAH are not known. PAHs of 60, 78, and 120 carbon atoms have UV absorbance spectra that show a discrete PAH electronic structure, but a PAH of 222 carbon atoms has Raman bands similar to those in graphite.

[edit] Occurrence and Production

It is now presumed that tiny fragments of graphene sheets are produced (along with quantities of other debris) whenever graphite is abraded, such as when drawing a line with a pencil.[2] However, it was physicists from University of Manchester and Institute for Microelectronics Technology, Chernogolovka, Russia who first isolated and studied graphene (rather than PAH) in 2004, and defined it in Science[3] as:

Graphene is the name given to a single layer of carbon atoms densely packed into a benzene-ring structure, and is widely used to describe properties of many carbon-based materials, including graphite, large fullerenes, nanotubes, etc. (e.g., carbon nanotubes are usually thought of as graphene sheets rolled up into nanometer-sized cylinders). Planar graphene itself has been presumed not to exist in the free state, being unstable with respect to the formation of curved structures such as soot, fullerenes, and nanotubes.

Graphene sheets in solid form (e.g. density > 1g/cc) usually show evidence in diffraction for graphite's 0.34 nm (002) layering. This is true even of some single-walled carbon nanostructures.[4] However, unlayered graphene with only (hk0) rings has been found in the core of presolar graphite onions.[5] Transmission electron microscope studies show faceting at defects in flat graphene sheets,[6] and suggest a possible role in this unlayered-graphene for two-dimensional dendritic crystallization from a melt.[7]

Graphene is presently one of the most expensive materials on Earth, with a sample that can be placed at the cross section of a human hair costing more than $1,000 (as of April 2008).[8] The price may fall dramatically, though, if commercial production methods are developed in the future.

[edit] Drawing Method

The British researchers obtained relatively large graphene sheets (eventually, up to 100 micrometres in size and visible through a magnifying glass) by mechanical exfoliation (repeated peeling) of 3D graphite crystals; their motivation was allegedly to study the electrical properties of thin graphite films and, as purely two-dimensional crystals were unknown before and presumed not to exist, their discovery of individual planes of graphite was presumably accidental. Both theory and experiment previously suggested that perfect 2D structures could not exist in the free state. It is believed that intrinsic microscopic roughening on the scale of 1 nm could be important for the stability of 2D crystals.[9]

Similar work is ongoing at many universities and the results obtained by the Manchester group in their PNAS paper "Two-dimensional atomic crystals" have been confirmed by several groups.[10] For an example of what graphene looks like, see its photograph below.

[edit] Epitaxial Growth

Another method uses the atomic structure of a substrate to seed the growth of the graphene, known as epitaxial growth. It doesn't typically yield a sample with a uniform thickness of graphene layers, and bonding between the bottom graphene layer and the substrate may affect the properties of the carbon layers. [11]

[edit] Silicon Carbide Reduction

Another method is to heat silicon carbide to high temperatures (1100°C) to reduce it to graphene. This process produces a sample size that is dependent upon the size of the SiC substrate used. Currently, SiC manufacturers have substrates for sale up to 4" in diameter. The face of the Silicon Carbide used for graphene creation, the silicon-terminated or carbon-terminated, highly influences the thickness, mobility and carrier density of the graphene. However, these substrates are very expensive (currently 1000's of dollars per wafer) and the substrate itself is not compatible with most fabrication techniques needed to create electronic devices.

[edit] Hydrazine Reduction

Researchers have developed a method of placing graphene oxide paper in a solution of pure hydrazine (a chemical compound of nitrogen and hydrogen), which reduces the graphene oxide paper into single-layer graphene.[12]

[edit] Sodium reduction of ethanol

A recent publication has described a process for producing gram-quantities of graphene, by the reduction of ethanol by sodium metal, followed by pyrolysis of the ethoxide product, and washing with water to remove sodium salts.[13]

[edit] Chemical Vapor Deposition

High-quality sheets of graphene exceeding 1 cm² (0.2 sq in) in area have been synthesized via chemical vapor deposition on thin nickel layers. [14] These sheets have been successfully transferred to various substrates, demonstrating viability for numerous electronic applications.

[edit] Properties

[edit] Atomic structure

The atomic structure of isolated, single-layer graphene was studied by transmission electron microscopy (TEM) on sheets of graphene suspended between bars of a metallic grid.[9] Electron diffraction patterns showed the expected hexagonal lattice of graphene. Suspended graphene also showed "rippling" of the flat sheet, with amplitude of about one nanometer. These ripples may be intrinsic to graphene as a result of the instability of two-dimensional crystals,[15][16][17] or may be extrinsic, originating from the ubiquitous dirt seen in all TEM images of graphene. Atomic resolution real-space images of isolated, single-layer graphene on silicon dioxide substrates were obtained[18][19] by scanning tunneling microscopy. Graphene processed using lithographic techniques is covered by photoresist residue, which must be cleaned to obtain atomic-resolution images.[18] Such residue may be the "adsorbates" observed in TEM images, and may explain the rippling of suspended graphene. Rippling of graphene on the silicon dioxide surface was determined by conformation of graphene to the underlying silicon dioxide, and not an intrinsic effect.[18]

[edit] Electronic properties

Graphene is quite different from most conventional three-dimensional materials. Intrinsic graphene is a semi-metal or zero-gap semiconductor. The E-k relation is linear for low energies near the six corners of the two-dimensional hexagonal Brillouin zone, leading to zero effective mass for electrons and holes. [20] Due to this linear “dispersion” relation at low energies, electrons and holes near these six points behave like relativistic particles described by the Dirac equation for spin 1/2 particles. [21] Hence, the electrons and holes are called Dirac fermions, and the six corners of the Brillouin zone are called the Dirac points.[20] The equation describing the E-k relation is E = \hbar v_F\sqrt{k_x^2+k_y^2}; where vf, the Fermi velocity, is approximately 106m / s.[21]

[edit] Electronic transport

Experimental results from transport measurements show that graphene has a remarkably high electron mobility at room temperature, with reported values in excess of 15,000 cm2V−1s−1. [17] Additionally, the symmetry of the experimentally measured conductance indicates that the mobilities for holes and electrons should be nearly the same.[20] The mobility is nearly independent of temperature between 10 K and 100 K,[22][23][24] which implies that the dominant scattering mechanism is defect scattering. Scattering by the acoustic phonons of graphene limits the room temperature mobility to 200,000 cm2V−1s−1 at a carrier density of 1012 cm−2[24][25]. The corresponding resistivity of the graphene sheet would be 10−6 Ω·cm, less than the resistivity of silver, the lowest resistivity substance known at room temperature[26]. However, for graphene on silicon dioxide substrates, scattering of electrons by optical phonons of the substrate is a larger effect at room temperature than scattering by graphene’s own phonons, and limits the mobility to 40,000 cm2V−1s−1.[24]

Despite the zero carrier density near the Dirac points, graphene exhibits a minimum conductivity on the order of 4e2 / h. The origin of this minimum conductivity is still unclear. However, rippling of the graphene sheet or ionized impurities in the SiO2 substrate may lead to local puddles of carriers that allow conduction.[20] Several theories suggest that the minimum conductivity should be 4e2 / hπ; however, most measurements are of order 4e2 / h or greater[17] and depend on impurity concentration.[27]

Recent experiments have probed the influence of chemical dopants on the carrier mobility in graphene.[28][27] Schedin, et al. doped graphene with various gaseous species (some acceptors, some donors), and found the initial undoped state of a graphene structure can be recovered by gently heating the graphene in vacuum. Schedin, et al. reported that even for chemical dopant concentrations in excess of 1012 cm−2 there is no observable change in the carrier mobility.[28]. Chen, et al. doped graphene with potassium in ultra high vacuum at low temperature. They found that potassium ions act as expected for charged impurities in graphene[29], and can reduce the mobility 20-fold.[27] The mobility reduction is reversible on heating the graphene to remove the potassium.

[edit] Optical properties

Photograph of graphene in transmitted light. This one atom thick crystal can be seen with the naked eye because it absorbs approximately 2.3% of white light, which is π times fine-structure constant.

Graphene's unique electronic properties produce an unexpectedly high opacity for an atomic monolayer, with a startlingly simple value: it absorbs πα ≈ 2.3% of white light, where α is the fine-structure constant.[30][31] This has been confirmed experimentally, but the measurement is not precise enough to improve on other techniques for determining the fine-structure constant.[32]

[edit] Spin transport

Graphene is thought to be an ideal material for spintronics due to small spin-orbit interaction and near absence of nuclear magnetic moments in carbon. Electrical spin-current injection and detection in graphene was recently demonstrated up to room temperature[33][34][35]. Spin coherence lengths greater than 1 micrometre at room temperature were observed[33], and control of the spin current polarity with an electrical gate was observed at low temperature[34].

[edit] Magnetic effects

Besides the high mobility and minimum conductivity, graphene shows very interesting behavior in the presence of a magnetic field. Graphene displays an anomalous quantum Hall effect with the sequence shifted by 1 / 2 with respect to the standard sequence. Thus, the Hall conductivity is \sigma_{xy} = \pm {4\left(N + 1/2 \right )e^2}/h , where N is the Landau level index and the double valley and double spin degeneracies give the factor of 4.[17] This remarkable behavior can even be measured at room temperature.[22] Bilayer graphene also shows the quantum Hall effect, but with the standard sequence where \sigma_{xy} = \pm {4Ne^2}/h . Interestingly, the first plateau at N = 0 is absent, indicating that bilayer graphene stays metallic at the neutrality point.[17]

Unlike normal metals, the longitudinal resistance of graphene shows maxima rather than minima for integral values of the Landau filling factor in measurements of the Shubnikov-de Haas oscillations, which show a phase shift of π, known as Berry’s phase.[20][22] The Berry’s phase arises due to the zero effective carrier mass near the Dirac points.[36] Study of the temperature dependence of the Shubnikov-de Haas oscillations in graphene reveals that the carriers have a non-zero cyclotron mass, despite their zero effective mass from the E-k relation.[22]

[edit] Nanostripes: Spin-polarized edge currents

Nanostripes of graphene (in the zig-zag orientation), at low temperatures, show spin-polarized edge currents [37], which also suggests applications in the recent field of spintronics.

[edit] Graphene oxide

By oxidising and chemically processing graphene, and then floating them in water, the graphene flakes form a single sheet and bond very powerfully. These sheets, called Graphene oxide paper have a measured tensile modulus of 32 GPa.[38]

[edit] Chemical modification

Soluble fragments of graphene can be prepared in the laboratory[39] through chemical modification of graphite. First, microcrystalline graphite is treated with a strongly acidic mixture of sulfuric acid and nitric acid. A series of steps involving oxidation and exfoliation result in small graphene plates with carboxyl groups at their edges. These are converted to acid chloride groups by treatment with thionyl chloride; next, they are converted to the corresponding graphene amide via treatment with octadecylamine. The resulting material (circular graphene layers of 5.3 angstrom thickness) is soluble in tetrahydrofuran, tetrachloromethane, and dichloroethane.

Hydrogenation of graphene results in graphane.[40]

[edit] Thermal properties

The near-room temperature thermal conductivity of graphene was recently measured to be between (4.84±0.44) ×103 to (5.30±0.48) ×103 Wm−1K−1. These measurements, made by a non-contact optical technique, are in excess of those measured for carbon nanotubes or diamond. It can be shown by using the Wiedemann-Franz law, that the thermal conduction is phonon-dominated.[41] However, for a gated graphene strip, an applied gate bias causing a Fermi Energy shift much larger than kBT can cause the electronic contribution to increase and dominate over the phonon contribution at low temperatures.[42]

Potential for this high conductivity can be seen by considering graphite, a 3D version of graphene that has basal plane thermal conductivity of over a 1000 W/mK (comparable to diamond). In graphite, the c-axis (out of plane) thermal conductivity is over a factor of ~100 smaller due to the weak binding forces between basal planes as well as the larger lattice spacing.[43] In addition, the ballistic thermal conductance of a graphene is shown to give the lower limit of the ballistic thermal conductances, per unit circumference, length of carbon nanotubes.[44]

Despite its 2-D nature, graphene has 3 acoustic phonon modes. The two in-plane modes have a linear dispersion relation, whereas the out of plane mode has a quadratic dispersion relation. Due to this, the T2 dependent thermal conductivity contribution of the linear modes is dominated at low temperatures by the T1.5 contribution of the out of plane mode.[44] The ballistic thermal conductance of graphene is isotropic.[42]

[edit] Mechanical properties

Graphene is the strongest substance known to man, according to a study released in August 2008 by Columbia University. However, the process of separating it from graphite, where it occurs naturally, will require some technological development before it is economical enough to be used in industrial processes.[45]

Utilizing an atomic force microscope, research has recently been able to measure the spring constant of suspended Graphene sheets. Graphene sheets, held together by van der Waals forces, were suspended over silicon dioxide cavities where an AFM tip was probed to test its mechanical properties. Its spring constant was measured to be on the order of 1-5 N/m and its Young's modulus was 0.5 TPa, which differs from bulk graphite. These high values make Graphene very strong and rigid. These intrinsic properties could lead to the possibility of utilizing Graphene for NEMS applications such as pressure sensors, and resonators.[46]

As is true of all materials, regions of graphene are subject to thermal and quantum fluctuations in relative displacement. Although the amplitude of these fluctuations is bounded in 3D structures (even in the limit of infinite size), the Mermin-Wagner theorem shows that the amplitude of long-wavelength fluctuations will grow logarithmically with the scale of a 2D structure, and would therefore be unbounded in structures of infinite size. Local deformation and elastic strain are negligibly affected by this long-range divergence in relative displacement. It is believed that a sufficiently large 2D structure, in the absence of applied lateral tension, will bend and crumple to form a fluctuating 3D structure. Researchers have observed ripples in suspended layers of graphene,[9] and it has been proposed that the ripples are caused by thermal fluctuations in the material. As a consequence of these dynamical deformations, it is debatable whether graphene is truly a 2D structure.[15][16][17]

[edit] Potential applications

[edit] Single molecule gas detection

Graphene makes an excellent sensor due to its 2D structure. The fact that its entire volume is exposed to its surrounding makes it very efficient to detect adsorbed molecules. Molecule detection is indirect: as a gas molecule adsorbs to the surface of graphene, the location of adsorption experiences a local change in electrical resistance. While this effect occurs in other materials, graphene is superior due to its high electrical conductivity (even when few carriers are present) and low noise which makes this change in resistance detectable.[28]

[edit] Graphene nanoribbons

Graphene nanoribbons (GNRs) are essentially single layers of graphene that are cut in a particular pattern to give it certain electrical properties. Depending on how the un-bonded edges are configured, they can either be in a Z (zigzag) or Armchair configuration. Calculations based on tight binding predict that zigzag GNRs are always metallic while armchairs can be either metallic or semiconducting, depending on their width. However, recent DFT calculations show that armchair nanoribbons are semiconducting with an energy gap scaling with the inverse of the GNR width. [47] Indeed, experimental results show that the energy gaps do increase with decreasing GNR width. [48] However, to date no experimental results have measured the energy gap of a GNR and identified the exact edge structure. [49] Zigzag nanoribbons are also semiconducting and present spin polarized edges. Their 2D structure, high electrical and thermal conductivity, and low noise also make GNRs a possible alternative to copper for integrated circuit interconnects. Some research is also being done to create quantum dots by changing the width of GNRs at select points along the ribbon, creating quantum confinement.[50]

Due to its high electronic quality, graphene has also attracted the interest of technologists who see them as a way of constructing ballistic transistors. Graphene exhibits a pronounced response to perpendicular external electric field allowing one to built FETs (field-effect transistors). In their 2004 paper,[3] the Manchester group demonstrated FETs with a "rather modest" on-off ratio of ~30 at room temperature. In 2006, Georgia Tech researchers announced that they had successfully built an all-graphene planar FET with side gates.[51] Their devices showed changes of 2% at cryogenic temperatures. The first top-gated FET (on-off ratio of <2) was demonstrated by researchers of AMICA and RWTH Aachen University in 2007 [52]. Graphene nanoribbons may prove generally capable of replacing silicon as a semiconductor in modern technology.[53]

[edit] New graphene devices

Facing the fact that current graphene transistors show a very poor on-off ratio, researchers are trying to find ways for improvement. In 2008 researchers of AMICA and University of Manchester demonstrated a new switching effect in graphene field-effect devices. This switching effect is based on a reversible chemical modification of the graphene layer and gives an on-off ratio of greater than six orders of magnitude. These reversible switches could potentially be applied to nonvolatile memories.[54]

In 2009 the Massachusetts Institute of Technology researchers built an experimental graphene chip known as a frequency multiplier. It is capable of taking an incoming electrical signal of a certain frequency and producing an output signal that is a multiple of that frequency. This graphene chip opens up a range of new applications, leading to various communications systems that can transmit data much faster than standard silicon chips.[55]

[edit] Integrated circuits

Graphene has the ideal properties to be an excellent component of integrated circuits. Graphene has a high carrier mobility, as well as low noise allowing it to be utilized as the channel in a FET. The issue is that single sheets of graphene are hard to produce, and even harder to make on top of an appropriate substrate. Researchers are looking into methods of transferring single graphene sheets from their source of origin (mechanical exfoliation on SiO2 / Si or thermal graphitization of a SiC surface) onto a target substrate of interest.[56] In 2008, the smallest transistor so far, one atom thick, 10 atoms wide was made of graphene[57]. IBM announced in December 2008 that they have fabricated and characterized graphene transistors operating at GHz frequencies.[58]


[edit] Transparent conducting electrodes

Graphene's high electrical conductivity and high optical transparency make it a candidate for transparent conducting electrodes, required for such applications as touchscreens, liquid crystal displays, organic photovoltaic cells, and OLEDs. In particular, graphene's mechanical strength and flexibility are advantageous compared to indium tin oxide, which is brittle, and graphene films may be deposited from solution over large areas[59][60].

[edit] Ultracapacitors

Due to the incredibly high surface area to mass ratio of graphene, one potential application is in the conductive plates of ultracapacitors. It is believed that graphene could be used to produce ultracapacitors with a greater energy storage density than is currently available[61].

[edit] Graphene biodevices

Graphene's modifiable chemistry, large surface area, atomic-thickness and molecularly-gatable structure make antibody-functionalized-graphene-sheets excellent candidate for mammalian and microbial detection and diagnosis[62].

[edit] Pseudo-relativistic theory

The electrical properties of graphene can be described by a conventional tight-binding model; in this model the energy of the electrons with wavenumber 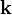\mathbf{k} is

E=\pm\sqrt{\gamma_0^2\left(1+4\cos^2{\pi k_ya}+4\cos{\pi k_ya} \cdot \cos{\pi k_x\sqrt{3}a}\right)} [63],

with the nearest-neighbour-hopping energy \gamma_0\approx 2{.}8\ \mathrm{eV} and the lattice constant a\approx 2{.}46\ \mathrm{\AA}. Conduction- and valence band, respectively, correspond to the different signs in the above dispersion relation; they touch each other in six points, the "K-values". However, only two of these six points are independent, whereas the rest is equivalent by symmetry. In the vicinity of the K-points the energy depends linearly on the wavenumber, similar to a relativistic particle. Since an elementary cell of the lattice has a basis of two atoms, the wave function even has an effective 2-spinor structure. As a consequence, at low energies, the electrons can be described by an equation which is formally equivalent to the Dirac equation. Moreover, in the present case this pseudo-relativistic description is restricted to the chiral limit, i.e., to vanishing rest mass M0, which leads to interesting additional features:

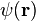v_F\vec\sigma\cdot\vec\nabla \psi(\mathbf{r})\,=\,E\psi(\mathbf{r})

Here v_F\approx 10^6\ \mathrm{m/s} is the Fermi velocity in graphene which replaces the velocity of light in the Dirac theory; \vec{\sigma} is the vector of the Pauli matrices, \psi(\mathbf{r}) is the two-component wave function of the electrons, and E their energy. [64]

[edit] History and experimental discovery

The term graphene first appeared in 1987[65] in order to describe single sheets of graphite as one of the constituents of graphite intercalation compounds (GICs); conceptually a GIC is a crystalline salt of the intercalant and graphene. The term was also used in early descriptions of carbon nanotubes,[66] as well as for epitaxial graphene,[67] and polycyclic aromatic hydrocarbons.[68] However, none of these examples constitutes isolated, two-dimensional graphene.

Larger graphene molecules or sheets (so that they can be considered as true isolated 2D crystals) cannot be grown even in principle. An article in Physics Today reads:

"Fundamental forces place seemingly insurmountable barriers in the way of creating [2D crystals] ... Nascent 2D crystallites try to minimize their surface energy and inevitably morph into one of the rich variety of stable 3D structures that occur in soot. But there is a way around the problem. Interactions with 3D structures stabilize 2D crystals during growth. So one can make 2D crystals sandwiched between or placed on top of the atomic planes of a bulk crystal. In that respect, graphene already exists within graphite ... One can then hope to fool Nature and extract single-atom-thick crystallites at a low enough temperature that they remain in the quenched state prescribed by the original higher-temperature 3D growth."[69]

Single layers of graphite were previously (starting from the 1970s) grown epitaxially on top of other materials.[70] This "epitaxial graphene" consists of a single-atom-thick hexagonal lattice of sp2-bonded carbon atoms, as in free-standing graphene. However, there is significant charge transfer from the substrate to the epitaxial graphene, and, in some cases, hybridization between the d orbitals of the substrate atoms and π orbitals of graphene, which significantly alters the electronic structure of the epitaxial graphene.

Single layers of graphite were also observed by transmission electron microscopy within bulk materials (see section Occurrence), in particular inside soot obtained by chemical exfoliation.[8] There have also been a number of efforts to make very thin films of graphite by mechanical exfoliation (starting from 1990 and continuing until after 2004)[8] but nothing thinner than 50 to 100 layers was produced during these years.

The previous efforts did not result in graphene as we know it now, i.e. as "free standing" single-atom-thick crystals of a macroscopic size which are either suspended or interact only weakly with a substrate. It is not important whether graphene is suspended or placed on another (non-binding) substrate. In both cases, it is isolated and can be studied as such. Within this definition of graphene, it was first isolated by the Manchester group of Andre Geim who in 2004[3] finally managed to extract single-atom-thick crystallites from bulk graphite. He provided the first and unexpected proof for the existence of true (free-standing) 2D crystals. Previously, it was assumed that graphene cannot exist in the flat state and should scroll into nanotubes "to decrease the surface energy".[71][72]

This experimental discovery of 2D crystal matter was openly doubted[3] until 2005 when in the same issue of Nature the groups of Andre Geim and Philip Kim of Columbia University have proved "beyond a reasonable doubt" that the obtained graphitic layers exhibit the electronic properties prescribed by theory. This theory was first developed by Philip R Wallace in 1947 as an approximation trying to understand the electronic properties of more complex, 3 dimensional graphite. He did not use the word graphene and referred to "a single hexagonal layer".[73] Later, graphene crystals obtained by using the Manchester recipe were also made suspended and their thickness proved directly by electron microscopy.[9]

[edit] References

  1. ^ C. D. Simpson et al. Synthesis of a Giant 222 Carbon Graphite Sheet. Chemistry - A European Journal, 6 1424 (2002)
  2. ^ "...bits of graphene are undoubtedly present in every pencil mark" —Carbon Wonderland, Scientific American, April 2008
  3. ^ a b c Novoselov, K.S. et al. Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666 (2004) doi:10.1126/science.1102896
  4. ^ D. Kasuya, M. Yudasaka, K. Takahashi, F. Kokai and S. Iijima (2002) J. Phys. Chem. B 106:4947.
  5. ^ T. J. Bernatowicz, R. Cowsik, P. C. Gibbons, K. Lodders, B. Fegley Jr., S. Amari, and R. S. Lewis (1996) Constraints on stellar grain formation from presolar graphite in the Murchison meteorite, Astrophysical Journal 472:760-782
  6. ^ P. Fraundorf and M. Wackenhut (2002) The core structure of presolar graphite onions, Astrophysical Journal Letters 578:L153-156 (astro-ph/0110585,cond-mat/0606093)
  7. ^ E. S. Mandell (2007) Electron beam characterization of carbon nanostructures, Dissertation in Physics (University of Missouri - Saint Louis and Rolla).
  8. ^ a b c "Carbon Wonderland", Scientific American, April 2008
  9. ^ a b c d Meyer, J. et al. The structure of suspended graphene sheets. Nature 446, 60-63 (1 March 2007)doi:10.1038/nature05545
  10. ^ Novoselov, K.S. et al. Two-dimensional atomic crystals. PNAS 102, 10451-10453 (January 26, 2005) doi:10.1073/pnas.0502848102
  11. ^ "A smarter way to grow graphene", PhysOrg.com, May 2008
  12. ^ "Researchers discover method for mass production of nanomaterial graphene", PhysOrg.com, Nov 2008
  13. ^ Choucair, Mohammad (2008). "Gram-scale production of graphene based on solvothermal synthesis and sonication". Nature Nanotechnology. doi:10.1038/nnano.2008.365. 
  14. ^ Kim; Yue Zhao, Houk Jang, Sang Yoon Lee, Jong Min Kim, Kwang S. Kim, Jong-Hyun Ahn, Philip Kim, Jae-Young Choi & Byung Hee Hong (January 14 2009). "Large-scale pattern growth of graphene films for stretchable transparent electrodes". Nature. doi:10.1038/nature07719. ISSN 0028-0836. http://www.nature.com/nature/journal/vaop/ncurrent/full/nature07719.html. 
  15. ^ a b Carlsson, J. M. Graphene: Buckle or break. Nature Materials, 6(11), 801-802 (2007)
  16. ^ a b Fasolino, A., Los, J. H., & Katsnelson, M. I. Intrinsic ripples in graphene. Nature Materials, 6(11), 858-861 (2007)
  17. ^ a b c d e f Geim, A. K. and Novoselov, K. S. The rise of graphene. Nature Mater. 6, 183-191 (2007)
  18. ^ a b c Ishigami, Masa; et al. (11 May 2007). "Atomic Structure of Graphene on SiO2" (PDF). Nano Lett. 7 (6): 1643–1648. doi:10.1021/nl070613a. http://pubs.acs.org/cgi-bin/article.cgi/nalefd/2007/7/i06/pdf/nl070613a.pdf. 
  19. ^ Stolyarova, Elena; et al. (21 May 2007). "High-resolution scanning tunneling microscopy imaging of mesoscopic graphene sheets on an insulating surface". Proceedings of the Natioanl Academy of Sciences 104: 9209–9212. doi:10.1073/pnas.0703337104. PMID 17517635. http://www.pnas.org/cgi/reprint/104/22/9209?maxtoshow=&HITS=10&hits=10&RESULTFORMAT=&fulltext=stolyarova&searchid=1&FIRSTINDEX=0&resourcetype=HWCIT. 
  20. ^ a b c d e J.-C. Charlier, P.C. Eklund, J. Zhu, and A.C. Ferrari, “Electron and Phonon Properties of Graphene: Their Relationship with Carbon Nanotubes,” from Carbon Nanotubes: Advanced Topics in the Synthesis, Structure, Properties and Applications, Ed. By A. Jorio, G. Dresselhaus, and M.S. Dresselhaus, Berlin/Heidelberg: Springer-Verlag, 2008
  21. ^ a b Avouris, P., Chen, Z., and Perebeinos, V. Carbon-based electronics. Nature Nano. 2 605-613 (2007)
  22. ^ a b c d Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197-200 (2005)
  23. ^ S.V. Morozov et al. Giant Intrinsic Carrier Mobilities in Graphene and Its Bilayer. Phys. Rev. Lett. 100, 016602 (2008)
  24. ^ a b c Chen, J. H. et al. Intrinsic and Extrinsic Performance Limits of Graphene Devices on SiO2. Nature Nanotechnology 3, 206-209 (2008)
  25. ^ Akturk, A. and Goldsman, N. Electron transport and full-band electron-phonon interactions in graphene. Journal of Applied Physics 103, 053702 (2008)
  26. ^ Physicists Show Electrons Can Travel More Than 100 Times Faster in Graphene[1]
  27. ^ a b c Chen, J. H. et al. Charged Impurity Scattering in Graphene. Nature Physics published online April 13, 2008
  28. ^ a b c Schedin, F. et al. Detection of individual gas molecules adsorbed on graphene. Nature Mater. 6, 652-655 (2007)
  29. ^ Adam, S. et al. A self-consistent theory for graphene transport. Proc. Nat. Acad. Sci. USA. 104, 18392-18397 (2007)
  30. ^ Kuzmenko, A. B.; van Heumen, E.; Carbone, F.; van der Marel, D. (2008), "Universal infrared conductance of graphite", Phys. Rev. Lett. 100: 117401(2008), doi:10.1103/PhysRevLett.100.117401 
  31. ^ Nair, R. R.; Blake, P.; Grigorenko, A. N.; Novoselov, K. S.; Booth, T. J.; Stauber, T.; Peres, N. M. R.; Geim, A. K. (2008-004-03), "Fine Structure Constant Defines Visual Transparency of Graphene", Science 320: 1308, doi:10.1126/science.1156965, PMID 18388259 
  32. ^ "Graphene Gazing Gives Glimpse Of Foundations Of Universe", ScienceDaily, 2008-04-04, http://www.sciencedaily.com/releases/2008/04/080403140918.htm, retrieved on 2008-04-06 
  33. ^ a b Tombros, Nikolaos; et al. (2 August 2007). "Electronic spin transport and spin precession in single graphene layers at room temperature" (PDF). Nature 448: 571–575. doi:10.1038/nature06037. 
  34. ^ a b Cho, Sungjae; Yung-Fu Chen, and Michael S. Fuhrer (19 September 2007). "Gate-tunable Graphene Spin Valve". Applied Physics Letters 91: 123105. doi:10.1063/1.2784934. 
  35. ^ Ohishi, Megumi; et al. (22 June 2007). "Spin Injection into a Graphene Thin Film at Room Temperature". Jpn. J. Appl. Phys. 46: L605–L607. doi:10.1143/JJAP.46.L605. 
  36. ^ Zhang, Y., Tan, Y. W., Stormer, H. L., and Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201-204 (2005)
  37. ^ See for example the PhD thesis of M. Wimmer, delivered to the physics faculty of the university of Regensburg in Sept. 2008.
  38. ^ Graphene Oxide Paper, Technology Transfer Program, Northwestern University
  39. ^ Sandip Niyogi, Elena Bekyarova, Mikhail E. Itkis, Jared L. McWilliams, Mark A. Hamon, and Robert C. Haddon . Solution Properties of Graphite and Graphene. J. Am. Chem. Soc. 128(24) pp. 7720–7721 (2006); (Communication) doi:10.1021/ja060680r
  40. ^ Control of Graphene's Properties by Reversible Hydrogenation: Evidence for Graphane D. C. Elias, R. R. Nair, T. M. G. Mohiuddin,1 S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim, K. S. Novoselov Science 30 January 2009: Vol. 323. no. 5914, pp. 610 - 613 doi:10.1126/science.1167130
  41. ^ Balandin, A.A., Ghosh, S., Bao, W., Calizo, I., Teweldebrahn, D., Miao, F., and Lau, C.N. "Superior Thermal Conductivity of Single-Layer Graphene", Nano Letters ASAP (2008)
  42. ^ a b Saito, K., Nakamura, J., and Natori, A. "Ballistic thermal conductance of a graphene sheet", Physical Review B 76 115409 (2007)
  43. ^ "Graphite and Precursors", By Pierre Delhaes
  44. ^ a b Mingo N., Broido, D.A. "Carbon Nanotube Ballistic Thermal Conductance and Its Limits" Physical Review Letters 95, 096105 (2005)
  45. ^ TOUGHEST STUFF KNOWN TO MAN: DISCOVERY OPENS DOOR TO SPACE ELEVATOR, By BILL SANDERSON, nypost.com, August 25, 2008 .
  46. ^ Frank, I. W., Tanenbaum, D. M., Van Der Zande, A.M., and McEuen, P. L. Mechanical properties of suspended graphene sheets. J. Vac. Sci. Technol. B 25, 2558-2561 (2007)
  47. ^ Barone, V., Hod, O., and Scuseria, G. E. Electronic Structure and Stability of Semiconducting Graphene Nanoribbons Nano Lett. 6, 2748 (2006)
  48. ^ Han., M.Y., Özyilmaz, B., Zhang, Y., and Kim, P. Energy Band-Gap Engineering of Graphene Nanoribbons. Phys. Rev. Lett. 98, 206805 (2007)
  49. ^ As of Thursday, February 28, 2008
  50. ^ Wang, Z. F., Shi, Q. W., Li, Q., Wang, X., Hou, J. G., Zheng, H., et al. Z-shaped graphene nanoribbon quantum dot device. Applied Physics Letters, 91(5), 053109 (2007)
  51. ^ Carbon-Based Electronics: Researchers Develop Foundation for Circuitry and Devices Based on Graphite March 14, 2006 gtresearchnews.gatech.edu Link
  52. ^ Lemme, M. C. et al A graphene field-effect device IEEE Electron Device Letters 28, 282 (2007) doi:10.1109/LED.2007.891668
  53. ^ Bullis, Kevin (2008-01-28). "Graphene Transistors". Technology Review (Cambridge: MIT Technology Review, Inc). http://www.technologyreview.com/Nanotech/20119/. Retrieved on 2008-02-18. 
  54. ^ Echtermeyer, Tim. J. et al Nonvolatile Switching in Graphene Field-Effect Devices IEEE Electron Device Letters 29, 952 (2008) doi:10.1109/LED.2008.2001179
  55. ^ "Graphene could lead to faster chips", PhysOrg.com, 2009-03-19, http://www.physorg.com/news156698836.html, retrieved on 2009-03-19 
  56. ^ Chen, J., Ishigami, M., Jang, C., Hines, D. R., Fuhrer, M. S., and Williams, E. D. Printed graphene circuits. Advanced Materials, 19(21), 3623-3627 (2007)
  57. ^ BBC News article of 17 April 2008; Ponomarenko et al, Science, 320, 356 (2008)
  58. ^ Graphene transistors clocked at 26 GHz Arxiv article
  59. ^ Wang, X.; et al. (11 December 2007). "Transparent, Conductive Graphene Electrodes for Dye-Sensitized Solar Cells". Nano Letters 8: 323. doi:10.1021/nl072838r. http://pubs.acs.org/cgi-bin/abstract.cgi/nalefd/2008/8/i01/abs/nl072838r.html. 
  60. ^ Eda G, Fanchini G, Chhowalla M (May 2008). "Large-area ultrathin films of reduced graphene oxide as a transparent and flexible electronic material". Nat Nanotechnol 3 (5): 270–4. doi:10.1038/nnano.2008.83. PMID 18654522. 
  61. ^ Stoller, Meryl D.; Sungjin Park, Yanwu Zhu, Jinho An, and Rodney S. Ruoff (22 August 2008) (PDF). Graphene-Based Ultracapacitors. http://bucky-central.me.utexas.edu/RuoffsPDFs/179.pdf. 
  62. ^ Mohanty, Nihar; Vikas Berry (2008). "Graphene-based Single-Bacterium Resolution Biodevice and DNA-Transistor - Interfacing Graphene-Derivatives with Nano and Micro Scale Biocomponents" (PDF). Nano Letters 8: 4469-76 (2008). http://pubs.acs.org/doi/abs/10.1021/nl802412n. 
  63. ^ P. R. Wallace, The Band Theory of Graphite, Physical Review 71 (1947) 622–634
  64. ^ A. H. Castro Neto, F. Guinea, N. M. R Peres, K. S. Novoselov, A. K. Geim, The electronic properties of graphene, e-print arXiv.org:0709.1163v2 , (2007), [2]
  65. ^ Mouras, S. ‘’et al.’’ Synthesis of first stage graphite intercalation compounds with fluorides. ‘’Revue de Chimie Minerale’’ ‘’’24’’’ 572 (1987).
  66. ^ Saito, R. ‘’et al.’’ Electronic structure of graphene tubules based on C60. ‘’Phys. Rev. B’’ ‘’’46’’’ 1804 (1992).
  67. ^ Forbeaux, I. ‘’et al.’’ Heteroepitaxial graphite on 6H-SiC(0001): Interface formation through conduction-band electronic structure. ‘’Phys. Rev. B’’ ‘’’58’’’ 16396 (1998).
  68. ^ Wang, S. ‘’et al.’’ A new carbonaceous material with large capacity and high efficiency for rechargeable Li-ion batteries. ‘’Journal of the Electrochemical Society’’. ‘’’147’’’, 2498 (2000).
  69. ^ Geim, A. K. & MacDonald, A. H. Graphene: Exploring carbon flatland. Physics Today, 60 35-41 (Aug 2007)
  70. ^ For a review, see Oshima, C. and Nagashima, A. Ultra-thin epitaxial films of graphite and hexagonal boron nitride on solid surfaces. J. Phys.: Condens. Matter 9, 1 (1997)
  71. ^ H. Shioyama J. Mater. Sci. Lett. 20, 499 (2001)
  72. ^ L. M. Viculis et al. Science 299, 1361 (2003)
  73. ^ P. R. Wallace, The Band Theory of Graphite, Physical Review 71 (1947) 622–634

[edit] See also

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Graphene"
Personal tools