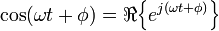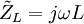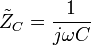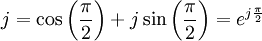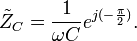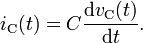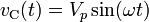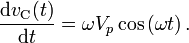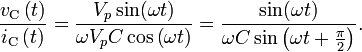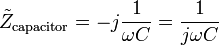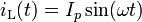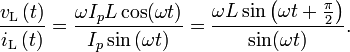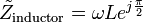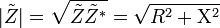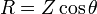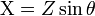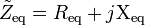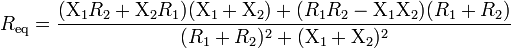Electrical impedance
From Wikipedia, the free encyclopedia

Electrical impedance, or simply impedance, describes a measure of opposition to a sinusoidal alternating current (AC). Electrical impedance extends the concept of resistance to AC circuits, describing not only the relative amplitudes of the voltage and current, but also the relative phases. Impedance is a complex quantity  and the term complex impedance may be used interchangeably; the polar form conveniently captures both magnitude and phase characteristics,
and the term complex impedance may be used interchangeably; the polar form conveniently captures both magnitude and phase characteristics,
where the magnitude 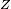 represents the ratio of the voltage difference amplitude to the current amplitude, while the argument
represents the ratio of the voltage difference amplitude to the current amplitude, while the argument  gives the phase difference between voltage and current and j is the imaginary unit. In Cartesian form,
gives the phase difference between voltage and current and j is the imaginary unit. In Cartesian form,
where the real part of impedance is the resistance 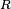 and the imaginary part is the reactance
and the imaginary part is the reactance 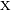 . Dimensionally, impedance is the same as resistance; the SI unit is the ohm. The term impedance was coined by Oliver Heaviside in July 1886.[1][2] Arthur Kennelly was the first to represent impedance with complex numbers in 1893.[3]
. Dimensionally, impedance is the same as resistance; the SI unit is the ohm. The term impedance was coined by Oliver Heaviside in July 1886.[1][2] Arthur Kennelly was the first to represent impedance with complex numbers in 1893.[3]
The reciprocal of impedance is admittance.
Contents |
[edit] Ohm's law
The meaning of electrical impedance can be understood by substituting it into Ohm's law.[4][5]
The magnitude of the impedance 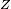 acts just like resistance, giving the drop in voltage amplitude across an impedance
acts just like resistance, giving the drop in voltage amplitude across an impedance  for a given current
for a given current 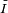 . The phase factor tells us that the current lags the voltage by a phase of θ (i.e. in the time domain, the current signal is shifted
. The phase factor tells us that the current lags the voltage by a phase of θ (i.e. in the time domain, the current signal is shifted  to the right with respect to the voltage signal).[6]
to the right with respect to the voltage signal).[6]
Just as impedance extends Ohm's law to cover AC circuits, other results from DC circuit analysis such as voltage division, current division, Thevenin's theorem, and Norton's theorem, can also be extended to AC circuits by replacing resistance with impedance.
[edit] Complex voltage and current
In order to simplify calculations, sinusoidal voltage and current waves are commonly represented as complex-valued functions of time denoted as  and
and 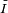 .[7][8]
.[7][8]
Impedance is defined as the ratio of these quantities.
Substituting these into Ohm's law we have
Noting that this must hold for all t, we may equate the magnitudes and phases to obtain
The magnitude equation is the familiar Ohm's law applied to the voltage and current amplitudes, while the second equation defines the phase relationship.
[edit] Validity of complex representation
This representation using complex exponentials may be justified by noting that (by Euler's formula):
i.e. a real-valued sinusoidal function (which may represent our voltage or current waveform) may be broken into two complex-valued functions. By the principle of superposition, we may analyse the behaviour of the sinusoid on the left-hand side by analysing the behaviour of the two complex terms on the right-hand side. Given the symmetry, we only need to perform the analysis for one right-hand term; the results will be identical for the other. At the end of any calculation, we may return to real-valued sinusoids by further noting that
In other words, we simply take the real part of the result.
[edit] Phasors
A phasor is a constant complex number, usually expressed in exponential form, representing the complex amplitude (magnitude and phase) of a sinusoidal function of time. Phasors are used by electrical engineers to simplify computations involving sinusoids, where they can often reduce a differential equation problem to an algebraic one.
The impedance of a circuit element can be defined as the ratio of the phasor voltage across the element to the phasor current through the element, as determined by the relative amplitudes and phases of the voltage and current. This is identical to the definition from Ohm's law given above, recognising that the factors of  cancel.
cancel.
[edit] Device examples

 , while the voltage across an inductor leads the current through it by
, while the voltage across an inductor leads the current through it by  . The identical voltage and current amplitudes tell us that the magnitude of the impedance is equal to one.
. The identical voltage and current amplitudes tell us that the magnitude of the impedance is equal to one.The impedance of a resistor is purely real and is referred to as a resistive impedance.
Inductors and capacitors have a purely imaginary reactive impedance.
Note the following identities for the imaginary unit and its reciprocal.
Thus we can rewrite the inductor and capacitor impedance equations in polar form
The magnitude tells us the change in voltage amplitude for a given current amplitude through our impedance, while the exponential factors give the phase relationship.
[edit] Deriving the device specific impedances
What follows below is a derivation of impedance for each of the three basic circuit elements, the resistor, the capacitor, and the inductor. Although the idea can be extended to define the relationship between the voltage and current of any arbitrary signal, these derivations will assume sinusoidal signals, since any arbitrary signal can be approximated as a sum of sinusoids through Fourier Analysis.
[edit] Resistor
For a resistor, we have the relation:
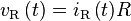 .
.
This is simply a statement of Ohm's Law.
Considering the voltage signal to be
it follows that
This tells us that the ratio of AC voltage amplitude to AC current amplitude across a resistor is R, and that the AC voltage leads the AC current across a resistor by 0 degrees.
This result is commonly expressed as
[edit] Capacitor
For a capacitor, we have the relation:
Considering the voltage signal to be
it follows that
And thus
This tells us that the ratio of AC voltage amplitude to AC current amplitude across a capacitor is  , and that the AC voltage leads the AC current across a capacitor by -90 degrees (or the AC current leads the AC voltage across a capacitor by 90 degrees).
, and that the AC voltage leads the AC current across a capacitor by -90 degrees (or the AC current leads the AC voltage across a capacitor by 90 degrees).
This result is commonly expressed in polar form, as
or, by applying Euler's formula, as
[edit] Inductor
For the inductor, we have the relation:
This time, considering the current signal to be
it follows that
And thus
This tells us that the ratio of AC voltage amplitude to AC current amplitude across an inductor is ωL, and that the AC voltage leads the AC current across an inductor by 90 degrees.
This result is commonly expressed in polar form, as
or, more simply, using Euler's formula, as
[edit] Resistance vs reactance
It is important to realize that resistance and reactance are not individually significant; together they determine the magnitude and phase of the impedance, through the following relations:
In many applications the relative phase of the voltage and current is not critical so only the magnitude of the impedance is significant.
[edit] Resistance
Resistance 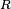 is the real part of impedance; a device with a purely resistive impedance exhibits no phase shift between the voltage and current.
is the real part of impedance; a device with a purely resistive impedance exhibits no phase shift between the voltage and current.
[edit] Reactance
Reactance 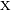 is the imaginary part of the impedance; a component with a finite reactance induces a phase shift θ between the voltage across it and the current through it.
is the imaginary part of the impedance; a component with a finite reactance induces a phase shift θ between the voltage across it and the current through it.
A reactive component is distinguished by the fact that the sinusoidal voltage across the component is in quadrature with the sinusoidal current through the component. This implies that the component alternately absorbs energy from the circuit and then returns energy to the circuit. A pure reactance will not dissipate any power.
[edit] Capacitive reactance
A capacitor has a purely reactive impedance which is inversely proportional to the signal frequency. A capacitor consists of two conductors separated by an insulator, also known as a dielectric.
At low frequencies a capacitor is open circuit, as no charge flows in the dielectric. A DC voltage applied across a capacitor causes charge to accumulate on one side; the electric field due to the accumulated charge is the source of the opposition to the current. When the potential associated with the charge exactly balances the applied voltage, the current goes to zero.
Driven by an AC supply, a capacitor will only accumulate a limited amount of charge before the potential difference changes sign and the charge dissipates. The higher the frequency, the less charge will accumulate and the smaller the opposition to the current.
[edit] Inductive reactance
An inductor has a purely reactive impedance which is proportional to the signal frequency. An inductor consists of a coiled conductor. Faraday's law of electromagnetic induction gives the back emf  (voltage opposing current) due to a rate-of-change of magnetic field
(voltage opposing current) due to a rate-of-change of magnetic field 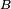 through a current loop.
through a current loop.
For an inductor consisting of a coil with N loops this gives.
The back-emf is the source of the opposition to current flow. A constant direct current has a zero rate-of-change, and sees an inductor as a short-circuit (it is typically made from a material with a low resistivity). An alternating current has a time rate-of-change that is proportional to frequency and so the inductive reactance is proportional to frequency.
[edit] Combining impedances
The total impedance of any network of components can be calculated using the rules for combining impedances in series and parallel. The rules are identical to those used for combining resistances, although they require some familiarity with complex numbers.
[edit] Series combination
For components connected in series, the current through each circuit element is the same; the ratio of voltages across any two elements is the inverse ratio of their impedances.
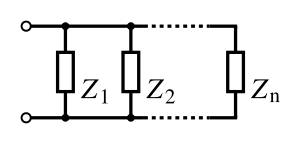
[edit] Parallel combination
For components connected in parallel, the voltage across each circuit element is the same; the ratio of currents through any two elements is the inverse ratio of their impedances.
The equivalent impedance  can be calculated in terms of the equivalent resistance
can be calculated in terms of the equivalent resistance  and reactance
and reactance 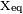 .[9]
.[9]
[edit] Measuring Impedance
According to Ohm’s law the impedance of a device can be calculated by complex division of the voltage and current. The impedance of the device can be calculated by applying a sinusoidal voltage to the device in series with a resistor, and measuring the voltage across the resistor and across the device. Performing this measurement by sweeping the frequencies of the applied signal provides the impedance phase and magnitude.[10]
[edit] Impulse impedance spectroscopy
The use of an impulse response may be used in combination with the fast Fourier transform (FFT) to rapidly measure the electrical impedance of various electrical devices. The technique compares well to other methodologies such as network and impedance analyzers while providing additional versatility in the electrical impedance measurement. The technique is theoretically simple, easy to implement and completed with ordinary laboratory instrumentation for minimal cost.[10]
[edit] References
- ^ Science, p. 18, 1888
- ^ Oliver Heaviside, The Electrician, p. 212, 23rd July 1886 reprinted as Electrical Papers, p64, AMS Bookstore, ISBN 0821834657
- ^ Kennelly, Arthur. Impedance (IEEE, 1893)
- ^ AC Ohm's law, Hyperphysics
- ^ Horowitz, Paul; Hill, Winfield (1989). "1". The Art of Electronics. Cambridge University Press. pp. 32–33. ISBN 0-521-37095-7.
- ^ Capacitor/inductor phase relationships, Yokogawa
- ^ Complex impedance, Hyperphysics
- ^ Horowitz, Paul; Hill, Winfield (1989). "1". The Art of Electronics. Cambridge University Press. pp. 31–32. ISBN 0-521-37095-7.
- ^ Parallel Impedance Expressions, Hyperphysics
- ^ a b Lewis Jr., George; George K. Lewis Sr. and William Olbricht (August 2008). "Cost-effective broad-band electrical impedance spectroscopy measurement circuit and signal analysis for piezo-materials and ultrasound transducers". Measurement Science and Technology 19: 105102. http://www.iop.org/EJ/abstract/0957-0233/19/10/105102/. Retrieved on 2008-09-15.
[edit] See also
- Admittance
- Impedance matching
- Impedance bridging
- Characteristic impedance
- Electrical load
- Negative impedance converter
[edit] External links
- Explaining Impedance
- Antenna Impedance
- ECE 209: Review of Circuits as LTI Systems – Brief explanation of Laplace-domain circuit analysis; includes a definition of impedance.


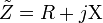

 , across a
, across a  .
.

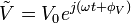


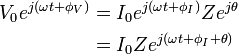


![\ \cos(\omega t + \phi) = \frac{1}{2} \Big[ e^{j(\omega t + \phi)} + e^{-j(\omega t + \phi)}\Big]](http://upload.wikimedia.org/math/e/3/6/e3688e571753ec6e4452f022cf76cf3e.png)