chi-square computationallinguistics dissertation dsp_algorithms hyptest ir likehood likelihood loglikelihood modeling research stat statistics

My tags:

From Wikipedia, the free encyclopedia

This article is in need of attention from an expert on the subject. WikiProject Statistics or the Statistics Portal may be able to help recruit one. (November 2008)

The likelihood ratio, often denoted by Λ (the capital Greek letter lambda), is the ratio of the maximum probability of a result under two different hypotheses. A likelihood-ratio test is a statistical test for making a decision between two hypotheses based on the value of this ratio.

Contents 1 Simple versus simple hypotheses 2 Definition (maximum likelihood ratio test for composite hypotheses) 2.1 Interpretation 2.2 Approximation 3 Examples 3.1 Medical 3.2 Coin tossing 4 Criticism 4.1 Theoretical 4.2 Practical 5 References 6 See also 6.1 Context 7 External links

[edit] Simple versus simple hypotheses

A statistical model is often a parametrized family of probability density functions or probability mass functions f(x;θ). A simple-vs-simple hypotheses test has completely specified models under both the null and alternative hypotheses, which for convenience are written in terms of fixed values of a notional parameter θ:

Note that under either hypothesis, the distribution of the data is fully specified; there are no unknown parameters to estimate. The likelihood ratio test statistic is^[1]:

Note that some references may use the reciprocal as the definition.^[2] In the form stated here, the likelihood ratio is large if the alternative model is better than the null model and the likelihood ratio test rejects the null hypothesis H₀ if the ratio exceeds a critical value c. That is, the decision rule has the form:

If Λ ≤ c accept H₀.

If Λ > c reject H₀.

The critical value c is usually chosen to obtain a specified significance level α, through the relation: P(Λ > c) = α (if x is discrete, some randomization on the boundary may be needed). The Neyman-Pearson lemma states that this likelihood ratio test is the most powerful among all level-α tests for this problem.

[edit] Definition (maximum likelihood ratio test for composite hypotheses)

A null hypothesis is often stated by saying the parameter θ is in a specified subset Θ₀ of the parameter space Θ. This is expressed by saying that the model being tested (the null model) is nested within the full model. The likelihood function is L(θ) = L(θ | x) = p(x | θ) = f_θ(x) is a function of the parameter θ with x held fixed at the value that was actually observed, i.e., the data. The likelihood ratio is

Many common test statistics such as the Z-test, the F-test, Pearson's chi-square test and the G-test are tests for nested models and can be phrased as log-likelihood ratios or approximations thereof.

In the above case, the null hypothesis is defined to be a model which is a special case of the alternative hypothesis, rather than a completely different statistical model. Often this can be done in a simple way by fixing some of the free parameters to values which define the subset model to be tested. However, caution must be taken to ensure that the remaining parameters are truly independent under this fixing. For example, if one is testing for the presence of an effect that implies changes to both location and spread within a dataset then the model's location parameter may be completely undefined under the hypothesis that the effect on the spread is zero.^{[dubious – discuss]}

[edit] Interpretation

Being a function of the data x, the LR is therefore a statistic. The likelihood-ratio test rejects the null hypothesis if the value of this statistic is too small. How small is too small depends on the significance level of the test, i.e., on what probability of Type I error is considered tolerable ("Type I" errors consist of the rejection of a null hypothesis that is true).

The numerator corresponds to the maximum probability of an observed result under the null hypothesis. The denominator corresponds to the maximum probability of an observed result under the alternative hypothesis. Under certain regularity conditions, the numerator of this ratio is less than the denominator. The likelihood ratio under those conditions is between 0 and 1. Lower values of the likelihood ratio mean that the observed result was less likely to occur under the null hypothesis. Higher values mean that the observed result was more likely to occur under the null hypothesis.

[edit] Approximation

If the distribution of the likelihood ratio corresponding to a particular null and alternative hypothesis can be explicitly determined then it can directly be used to form decision regions (to accept/reject the null hypothesis). In most cases, however, the exact distribution of the likelihood ratio corresponding to specific hypotheses is very difficult to determine. A convenient result, though, says that as the sample size n approaches 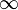, the test statistic − 2log(Λ) for a nested model will be asymptotically χ² distributed with degrees of freedom equal to the difference in dimensionality of Θ and Θ₀. This means that for a great variety of hypotheses, a practitioner can compute the likelihood ratio Λ for the data and compare − 2log(Λ) to the chi squared value corresponding to a desired statistical significance as an approximate statistical test.

[edit] Examples

[edit] Medical

One example of a likelihood ratio would be the likelihood that a given test result would be expected in a patient with a certain disorder compared to the likelihood that same result would occur in a patient without the target disorder.

Some sources distinguish between LR+ and LR-.^[3] A worked example is shown below.

Relationships among terms

		Condition (as determined by "Gold standard")
		Positive	Negative
Test outcome	Positive	True Positive	False Positive (Type I error, P-value)	→ Positive predictive value
	Negative	False Negative (Type II error)	True Negative	→ Negative predictive value
		↓ Sensitivity	↓ Specificity

A worked example

the Fecal occult blood (FOB) screen test is used in 203 people to look for bowel cancer:

		Patients with bowel cancer (as confirmed on endoscopy)
		Positive	Negative	?
FOB test	Positive	TP = 2	FP = 18	= TP / (TP + FP) = 2 / (2 + 18) = 2 / 20 ≡ 10%
	Negative	FN = 1	TN = 182	= TN / (TN + FN) 182 / (1 + 182) = 182 / 183 ≡ 99.5%
		↓ = TP / (TP + FN) = 2 / (2 + 1) = 2 / 3 ≡ 66.67%	↓ = TN / (FP + TN) = 182 / (18 + 182) = 182 / 200 ≡ 91%

Related calculations

• False positive rate (α) = FP / (FP + TN) = 18 / (18 + 182) = 9% = 1 - specificity
• False negative rate (β) = FN / (TP + FN) = 1 / (2 + 1) = 33% = 1 - sensitivity
• Power = sensitivity = 1 − β
• Likelihood-ratio positive = sensitivity / (1 - specificity) = 66.67% / (1 - 91%) = 7.4
• Likelihood-ratio negative = (1 - sensitivity) / specificity = (1 - 66.67%) / 91% = .73

Hence with large numbers of false positives and few false negatives, a positive FOB screen test is in itself poor at confirming cancer (PPV=10%) and further investigations must be undertaken, it will though pickup 66.7% of all cancers (the sensitivity). However as a screening test, a negative result is very good at reassuring that a patient does not have cancer (NPV=99.5%) and at this initial screen correctly identifies 91% of those who do not have cancer (the specificity).

[edit] Coin tossing

An example, in the case of Pearson's test, we might try to compare two coins to determine whether they have the same probability of coming up heads. Our observation can be put into a contingency table with rows corresponding to the coin and columns corresponding to heads or tails. The elements of the contingency table will be the number of times the coin for that row came up heads or tails. The contents of this table are our observation X.

	Heads	Tails
Coin 1	k1H	k1T
Coin 2	k2H	k2T

Here Θ consists of the parameters p_1H, p_1T, p_2H, and p_2T, which are the probability that coin 1 (2) comes up heads (tails). The hypothesis space H is defined by the usual constraints on a distribution, , and p_iH + p_iT = 1. The null hypothesis H₀ is the sub-space where p_1j = p_2j. In all of these constraints, i = 1,2 and j = H,T.

Writing n_ij for the best values for p_ij under the hypothesis H, maximum likelihood is achieved with

Writing m_ij for the best values for p_ij under the null hypothesis H₀, maximum likelihood is achieved with

which does not depend on the coin i.

The hypothesis and null hypothesis can be rewritten slightly so that they satisfy the constraints for the logarithm of the likelihood ratio to have the desired nice distribution. Since the constraint causes the two-dimensional H to be reduced to the one-dimensional H₀, the asymptotic distribution for the test will be χ²(1), the χ² distribution with one degree of freedom.

For the general contingency table, we can write the log-likelihood ratio statistic as

[edit] Criticism

[edit] Theoretical

Bayesian criticisms of classical likelihood ratio tests focus on two issues:^{[citation needed]}

1. the supremum function in the calculation of the likelihood ratio, saying that this takes no account of the uncertainty about θ and that using maximum likelihood estimates in this way can promote complicated alternative hypotheses with an excessive number of free parameters;
2. testing the probability that the sample would produce a result as extreme or more extreme under the null hypothesis, saying that this bases the test on the probability of extreme events that did not happen.

Instead they put forward methods such as Bayes factors, which explicitly take uncertainty about the parameters into account, and which are based on the evidence that did occur. This criticism ignores the point that, in practice, likelihood ratio tests are used as the basis of confidence intervals, which do reflect the uncertainty about θ. It also ignores the fact that likelihood ratio tests provide a practicable approach to statistical inference which is usually readily applicable.

[edit] Practical

In medicine, the use of likelihood ratio tests has been promoted to assist in interpreting diagnostic tests^[4]. A large likelihood ratio, for example a value more than 10, helps rule in disease. A small likelihood ratio, for example a value less than 0.1, helps rule out disease^[5]. However, physicians rarely make these calculations^[6] and sometimes make errors when they do attempt calculations.^[7] A randomized controlled trial compared how well physicians interpreted diagnostic tests that were presented as either sensitivity and specificity, a likelihood ratio, or an inexact graphic of the likelihood ratio, found no difference in ability to interpret test results.^[8]

[edit] References

[edit] See also

• Bayes factor, Bayesian analog

[edit] Context

• Likelihood function
• Likelihood principle
• Score function

[edit] External links

• Practical application of Likelihood-ratio test described
• Vassar College's Likelihood Ratio Given Sensitivity/Specifity/Prevalence Online Calculator