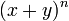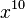Binomial theorem
From Wikipedia, the free encyclopedia

In mathematics, the binomial theorem is an important formula giving the expansion of powers of sums. Its simplest version states that
for any real or complex numbers x and y, and any non-negative integer n. The binomial coefficient appearing in (1) may be defined in terms of the factorial function n!:
For example, here are the cases where 2 ≤ n ≤ 5:
Formula (1) is valid more generally for any elements x and y of a semiring as long as xy = yx. (The theorem is true even more generally: note that associativity is not required, just alternativity).
Contents |
[edit] History
This formula and the triangular arrangement of the binomial coefficients are often attributed to Blaise Pascal, who described them in the 17th century, but they were known to many mathematicians who preceded him. The 4th century B.C. Greek mathematician Euclid knew a special case of the binomial theorem up to the second order,[1][2] as did the 3rd century B.C. Indian mathematician Pingala to higher orders. A more general binomial theorem and the so-called "Pascal's triangle" were known to the 10th-century A.D. Indian mathematician Halayudha, the 11th-century A.D. Persian mathematician Omar Khayyám, and 13th-century Chinese mathematician Yang Hui, who all derived similar results.[3]
[edit] Simple derivation
Consider a = (x + y)n . a can be written as a product of sums,  , where each si = x + y . The expansion of a is the sum of all products involving one term—either x or y—from each si . For example, the term xn in the expansion of a is had by picking x in each si .
, where each si = x + y . The expansion of a is the sum of all products involving one term—either x or y—from each si . For example, the term xn in the expansion of a is had by picking x in each si .
The coefficient of each term in the expansion of a is determined by how many different ways there are to pick terms from the si such that their product is of the same form as the term (excluding the coefficient). Consider t = xn − 1y. t can be formed from a by picking y from one of the si and x in the rest of them. There are n ways to pick a si to provide the y; t is thus formed in n different ways in the expansion of a, making its coefficient n. In general, for t = xn − kyk, there are
different ways to pick the si that provide the ys (since k ys are picked from the n si), and thus this must be the coefficient for t. The binomial theorem follows naturally from here.
[edit] Newton's generalized binomial theorem
Around 1665, Isaac Newton generalized the formula to allow exponents other than nonnegative integers. In this generalization, the finite sum is replaced by an infinite series. Namely, if x and y are real numbers with x > |y|,[4] and r is any complex number, then
When r is a nonnegative integer, the binomial coefficients for k > r are zero, so (2) specializes to (1), and there are at most r+1 nonzero terms. For other values of r, the series (2) has an infinite number of nonzero terms, at least if x and y are nonzero.
The coefficients can also be written
where  is the Pochhammer symbol. This is important when one is working with infinite series and would like to represent them in terms of generalized hypergeometric functions. This form is used in applied mathematics, for example, when evaluating the formulas that model the statistical properties of the phase-front curvature of a light wave as it propagates through optical atmospheric turbulence.[citation needed]
is the Pochhammer symbol. This is important when one is working with infinite series and would like to represent them in terms of generalized hypergeometric functions. This form is used in applied mathematics, for example, when evaluating the formulas that model the statistical properties of the phase-front curvature of a light wave as it propagates through optical atmospheric turbulence.[citation needed]
Taking r = −s leads to a particularly handy but non-obvious formula:
Further specializing to s = 1 yields the geometric series formula.
[edit] Generalizations
Formula (2) can be generalized to the case where x and y are complex numbers. For this version, one should assume |x| > |y|[4] and define the powers of x+y and x using a holomorphic branch of log defined on an open disk of radius |x| centered at x.
Formula (2) is valid also for elements x and y of a Banach algebra as long as xy = yx, x is invertible, and ||y/x|| < 1.
For a more extensive account of Newton's generalized binomial theorem, see binomial series.
[edit] "Binomial type"
The binomial theorem can be stated by saying that the polynomial sequence
is of binomial type.
[edit] Proof
One way to prove the binomial theorem (1) is with mathematical induction. When n = 0, we have
For the inductive step, assume the theorem holds when the exponent is m. Then for n = m + 1
by the inductive hypothesis
by multiplying through by a and b
by pulling out the k = 0 term
by letting j = k − 1
by pulling out the k = m + 1 term from the right hand side
by combining the sums
from Pascal's rule
by adding in the 0 and m + 1 terms.
[edit] Binomial number
A binomial number is a number in the form of  (for n at least 2). When the sign is minus or n is odd these binomial numbers can be factored algebraically:
(for n at least 2). When the sign is minus or n is odd these binomial numbers can be factored algebraically:
Examples:
To factor  simply, use
simply, use
[edit] A quick way to expand binomials
To quickly expand binomials of the form
The first term is
(this follows directly from the generalized binomial theorem) and the coefficient of each subsequent term is the current coefficient multiplied by the current exponent of x, divided by the current term number. Exponents of x decrease each term, while exponents of y increase each term (from 0 in the first term) until the exponent of x is 0 and that of y is n.
Example:
The first term is
To find the coefficient of the second term, multiply 1 (the current coefficient) by 10 (the current exponent of x), and divide by the current term number (1, since this is the first term) to get 10. The exponent of x decrements, and the exponent of y increments. The next term is therefore
Similarly, the next coefficient is (10×9)/(2×1), which gives 45. After that, it is (10×9×8)/(3×2×1). This continues until (10×9×8×7×6)/(5×4×3×2×1), after which, the coefficients are symmetrical. The whole thing is
- x10 + 10x9y + 45x8y2 + 120x7y3 + 210x6y4 + 252x5y5 + 210x4y6 + 120x3y7 + 45x2y8 + 10xy9 + y10.
Notice that the coefficients are perfectly symmetrical. This will happen when the coefficients of x and y within the parentheses of the original expression are the same. Recognizing this can save even more time.
More formally, given a term
The next term in the binomial is
If the original expression instead was
then the resulting expansion would be the same, except with (2x) in place of x in every place. The factor of 2 must get raised to the power of x in each term. The same holds true if either x or y is raised to a power inside the parentheses of the original expression.
[edit] The binomial theorem in popular culture
- In the Sherlock Holmes books, the villain Professor Moriarty is the author of A Treatise on the Binomial Theorem.
- The binomial theorem is mentioned in the Gilbert and Sullivan song "I am the Very Model of a Modern Major General".
- The binomial theorem appears in at least three different works by Monty Python - Coal Mine in Llandarogh Carmarthen, The Tale of Happy Valley, and the film Monty Python's The Meaning of Life.
- The binomial theorem is mentioned in the TV series NUMB3RS in episode #217 ("Mind Games") in Season 2.
- Contrary to popular belief, the generalized binomial theorem is not engraved on Isaac Newton's tomb in Westminster Abbey.[5]
- In chapter 18 of Mikhail Bulgakov's "The Master and Margarita", the black magic practitioner Woland says, "But by Newton's binomial theorem, I predict that he will die in nine month's time..." From this, "it's hardly Newton's binomial theorem" became a popular Russian expression.
- There is a short poem by Álvaro de Campos, heteronym of the Portuguese writer Fernando Pessoa about the binomial theorem that roughly translates into: "Newton's binomial is as beautiful as the Venus de Milo. The truth is few people notice it."
- In record 5 of Yevgeny Zamyatin's We, the protagonist D-503 says, "...to me it's nothing more than the four equal angles, but for you that might be, I don't know, as tough as Newton's binomial theorem."
[edit] See also
| The Wikibook Combinatorics has a page on the topic of |
- Binomial distribution
- Binomial probability
- Binomial inverse theorem
- Binomial series
- Combination
- Stirling's approximation
- Multinomial theorem
- Negative binomial distribution
- Pascal's triangle
[edit] Notes
- ^ Binomial Theorem
- ^ The Story of the Binomial Theorem, by J. L. Coolidge, The American Mathematical MonthlyVol. 56, No. 3 (Mar., 1949), pp. 147-157
- ^ Landau, James A (1999-05-08). "Historia Matematica Mailing List Archive: Re: [HM] Pascal's Triangle" (mailing list email). Archives of Historia Matematica. http://archives.math.utk.edu/hypermail/historia/may99/0073.html. Retrieved on 2007-04-13.
- ^ a b This is to guarantee convergence. Depending on r, the series may also converge sometimes when |x| = |y|.
- ^ Cajori, Florian (1985). 'A History of Mathematics'. New York: Chelsea Publishing Company. pp. 205. ISBN 0-8284-1303-X.
[edit] References
- Amulya Kumar Bag. Binomial Theorem in Ancient India. Indian J.History Sci.,1:68-74,1966.
[edit] External links
- Binomial Theorem by Stephen Wolfram, and "Binomial Theorem (Step-by-Step)" by Bruce Colletti and Jeff Bryant, Wolfram Demonstrations Project, 2007.
This article incorporates material from inductive proof of binomial theorem on PlanetMath, which is licensed under the GFDL.




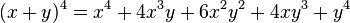
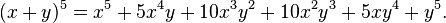
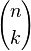
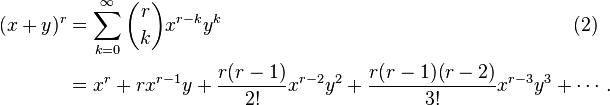










![= a^{m+1} + b^{m+1} + \sum_{k=1}^m \left[ { m \choose k } + { m \choose k-1 } \right] a^{m+1-k}b^k](http://upload.wikimedia.org/math/e/f/9/ef90c26a2f2ead76ee476e7b18068b98.png)