Gamut
From Wikipedia, the free encyclopedia

The grayed-out horseshoe shape is the entire range of possible chromaticities. The colored triangle is the gamut available to a typical computer monitor; it does not cover the entire space. The corners of the triangle are the primary colors for this gamut; in the case of a CRT, they depend on the colors of the phosphors of the monitor. At each point, the brightest possible RGB color of that chromaticity is displayed, resulting in the bright Mach band stripes corresponding to the edges of the RGB color cube.
In color reproduction, including computer graphics and photography, the gamut, or color gamut (pronounced /ˈgæmət/), is a certain complete subset of colors. The most common usage refers to the subset of colors which can be accurately represented in a given circumstance, such as within a given color space or by a certain output device. Another sense, less frequently used but not less correct, refers to the complete set of colors found within an image at a given time. In this context, digitizing a photograph, converting a digitized image to a different color space, or outputting it to a given medium using a certain output device generally alters its gamut, in the sense that some of the colors in the original are lost in the process.
Contents |
[edit] Introduction
The term gamut was adopted from the field of music, where it means the set of pitches of which musical melodies are composed; Shakespeare's use of the term in The Taming of the Shrew is sometimes attributed to the author/musician, Thomas Morley.[1] In the 1850s, the term was applied to a range of colors or hue, for example by Thomas De Quincey who wrote, "Porphyry, I have heard, runs through as large a gamut of hues as marble."[2]
In color theory, the gamut of a device or process is that portion of the color space that can be represented, or reproduced. Generally, the color gamut is specified in the hue–saturation plane, as many systems can produce colors over a wide intensity range within their color gamut; in addition, for subtractive color systems, such as printing, the range of intensity available in the system is for the most part meaningless outside the context of its illumination.
When certain colors cannot be displayed within a particular color model, those colors are said to be out of gamut. For example, pure red which is contained in the RGB color model gamut is out of gamut in the CMYK model.
A device that is able to reproduce the entire visible color space is somewhat of a holy grail in the engineering of color displays and printing processes. While modern techniques allow increasingly good approximations, the complexity of these systems often makes them impractical. What is "good enough" is dictated by the limitations of human perception.
While processing a digital image, the most convenient color model used is the RGB model. Printing the image requires transforming the image from the original RGB color space to the printer's CMYK color space. During this process, the colors from the RGB which are out of gamut must be somehow converted to approximate values within the CMYK space gamut. Simply trimming only the colors which are out of gamut to the closest colors in the destination space would burn the image. There are several algorithms approximating this transformation, but none of them can be truly perfect, since those colors are simply out of the target device's capabilities. This is why identifying the colors in an image which are out of gamut in the target color space as soon as possible during processing is critical for the quality of the final product.
[edit] Representation of gamuts
Gamuts are commonly represented as areas in the CIE 1931 chromaticity diagram as shown at right, with the curved edge representing the monochromatic colors. Gamut areas typically have triangular shapes because most color reproduction is done with three primaries.
However, the accessible gamut depends on the brightness; a full gamut must therefore be represented in 3D space, as below:
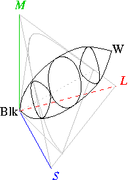
The pictures at left show the gamuts of RGB color space (top), such as on computer monitors, and of reflective colors in nature (bottom). The cone drawn in grey corresponds roughly to the CIE diagram at right, with the added dimension of brightness.
The axes in these diagrams are the responses of the short-wavelength (S), middle-wavelength (M), and long-wavelength (L) cones in the human eye. The other letters indicate black (Blk), red (R), green (G), blue (B), cyan (C), magenta (M), yellow (Y), and white colors (W). (Note: These pictures are not exactly to scale.)
The left diagram shows that the shape of the RGB gamut is a triangle between red, green, and blue at lower luminosities; a triangle between cyan, magenta, and yellow at higher luminosities, and a single white point at maximum luminosity. The exact positions of the apexes depends on the emission spectra of the phosphors in the computer monitor, and on the ratio between the maximum luminosities of the three phosphors (i.e., the color balance).
The gamut of the CMYK color space is, ideally, approximately the same as that for RGB, with slightly different apexes, depending on both the exact properties of the dyes and the light source. In practice, due to the way raster-printed colors interact with each other and the paper and due to their non-ideal absorption spectra, the gamut is smaller and has rounded corners.
The gamut of reflective colors in nature has a similar, though more rounded, shape. An object that reflects only a narrow band of wavelengths will have a color close to the edge of the CIE diagram, but it will have a very low luminosity at the same time. At higher luminosities, the accessible area in the CIE diagram becomes smaller and smaller, up to a single point of white, where all wavelengths are reflected exactly 100 per cent. The exact coordinates of white are of course determined by the color of the light source.
[edit] Limitations of color representation
[edit] Surfaces

In the beginning of the 20th century industrial demands for a controllable way to describe colors and the new possibility to measure light spectra initiated intense research on mathematical descriptions of colors. The idea of optimal colors was introduced by the Baltic German Chemist Wilhelm Ostwald. Erwin Schrödinger showed in his 1919 article Theorie der Pigmente von größter Leuchtkraft (Theory of Pigments with Highest Luminosity)[3] that the most-saturated colors are generated by stimuli having either a zero or full reflectance over the visible spectrum. (i.e., the reflectivity spectrum must have at most two transitions). Thus two types of optimal color spectra are possible: Either the transition goes from zero at both ends of the spectrum to one in the middle, as shown in the image, or it goes from one at the ends to zero in the middle. The first type produces colors that are similar to the spectral colors and follow roughly the horseshoe-shaped portion of the CIE xy chromaticity diagram. The second type produces colors that are similar to the colors near the straight line in the CIE xy chromaticity diagram, leading to magenta-like colors. Schrödinger's work was further developed by David MacAdam and Siegfried Rösch.[4] MacAdam was the first person to calculate precise coordinates of selected points on the boundary of the optimal color solid in the CIE 1931 color space for lightness levels from Y = 10 to 95 in steps of 10 units. This enabled him to draw the optimal color solid at an acceptable degree of precision. Because of his achievement the boundary of the optimal color solid is called the MacAdam limit. Today efficient algorithms can calculate the boundary to a much higher degree of precision (several hundred points per lightness level compared to MacAdam's maximum of twelve points per level) in an acceptable amount of time (an hour on a modern computer). The MacAdam limit, on which the most saturated (or "optimal") colors reside, shows that colors that are near monochromatic colors can only be achieved at very low luminance levels, except for yellows, because a mixture of the wavelengths from the long straight-line portion of the spectral locus between green and red will combine to make a color very close to a monochromatic yellow.
[edit] Light sources
Light sources used as primaries in an additive color reproduction system need to be bright, so they are generally not close to monochromatic. That is, the color gamut of most light sources can be understood as a result of difficulties producing pure monochromatic (single wavelength) light. The best technological source of (nearly) monochromatic light is the laser, which is expensive and impractical for many systems (as laser technology improves and becomes more inexpensive, this may no longer be the case). Other than lasers, most systems represent highly saturated colors with a more or less crude approximation, which includes light with a range of wavelengths besides the desired color. This may be more pronounced for some hues than others.
Systems which use additive color processes usually have a color gamut which is roughly a convex polygon in the hue-saturation plane. The vertices of the polygon are the most saturated colors the system can produce. In subtractive color systems, the color gamut is more often an irregular region.
[edit] Comparison of various systems
| This section needs additional citations for verification. Please help improve this article by adding reliable references (ideally, using inline citations). Unsourced material may be challenged and removed. (April 2007) |
Following is a list of representative color systems more or less ordered from large to small color gamut:
- Laser video projector uses 3 lasers to produce the broadest gamut available in practical display equipment today, derived from the fact that lasers produce truly monochromatic primaries. The systems work either by scanning the entire picture a dot at a time and modulating the laser directly at high frequency, much like the electron beams in a CRT, or by optically spreading and then modulating the laser and scanning a line at a time, the line itself being modulated in much the same way as in a DLP. Lasers can also be used as a light source for a DLP. More than 3 lasers can be combined to increase the gamut range, a technique sometimes used in holography.[5]
- Photographic film can reproduce a larger color gamut than typical television, computer, or home video systems.[6]
- CRT and similar video displays have a roughly triangular color gamut which covers a significant portion of the visible color space. In CRTs, the limitations are due to the phosphors in the screen which produce red, green, and blue light.
- Liquid crystal display (LCD) screens filter the light emitted by a backlight. The gamut of an LCD screen is therefore limited to the emitted spectrum of the backlight. Typical LCD screens use cold-cathode fluorescent bulbs (CCFL's) for backlights. LCD Screens with certain LED or wide-gamut CCFL backlights yield a more comprehensive gamut than CRTs.
- Television uses a CRT display (usually), but does not take full advantage of its color display properties, due to the limitations of broadcasting. HDTV is far better, but still somewhat less than, for example, computer displays using the same display technology.
- Paint mixing, both artistic and for commercial applications, achieves a reasonably large color gamut by starting with a larger palette than the red, green, and blue of CRTs or cyan, magenta, and yellow of printing. Paint may reproduce some highly saturated colors that cannot be reproduced well by CRTs (particularly violet), but overall the color gamut is smaller.[citation needed]
- Printing typically uses the CMYK color space (cyan, magenta, yellow, and black). Very few printing processes do not include black; however, those processes (with the exception of dye-sublimation printers) are poor at representing low saturation, low intensity colors. Efforts have been made to expand the gamut of the printing process by adding inks of non-primary colors; these are typically orange and green (see Hexachrome) or light cyan and light magenta. Spot color inks of a very specific color are also sometimes used.
- A monochrome display's color gamut is a one-dimensional curve in color space.
[edit] References
- ^ John H. Long (January 1950). "Shakespeare and Thomas Morley". http://links.jstor.org/sici?sici=0149-6611(195001)65%3A1%3C17%3ASATM%3E2.0.CO%3B2-L.
- ^ Thomas De Quincey (1854). De Quincey's works. James R. Osgood. http://books.google.com/books?id=5TACAAAAQAAJ&pg=PA36&dq=gamut-of-hues+date:0-1856#PPA35,M1.
- ^ Schrödinger, Erwin (1919). "Theorie der Pigmente größter Leuchtkraft". Annalen der Physik 367 (15): 603–622. doi:.
- ^ Lee, Hsien-Che (2005). "18.7: Theoretical color gamut". Introduction to Color Imaging Science. Cambridge University Press. p. 468. ISBN 052184388X. http://books.google.com/books?id=CzAbJrLin_AC&pg=PA469&dq=Introduction+to+Color+Imaging+Science+%22optimal+color%22&ei=x8uwR9K4O5fayASsgtTnAg&sig=JySKyjSb0fVyWC0jmAOL7mZXsEg.
- ^ "Color holography to produce highly realistic three-dimensional images". http://www.opticsinfobase.org/abstract.cfm?URI=ao-47-4-A123.
- ^ "Film gamut, apples, and oranges". http://www.gamutvision.com/docs/camera_scanner.html. Retrieved on 2007-04-26.
[edit] External links
- Using the Chromaticity Diagram for Color Gamut Evaluation by Bruce Lindbloom.
- Color Gamut Mapping book by Jan Morovic.
- Quantifying Color Gamut by William D. Kappele