SHA hash functions
From Wikipedia, the free encyclopedia
The SHA hash functions are a set of cryptographic hash functions designed by the National Security Agency (NSA) and published by the NIST as a U.S. Federal Information Processing Standard. SHA stands for Secure Hash Algorithm. The three SHA algorithms are structured differently and are distinguished as SHA-0, SHA-1, and SHA-2. The SHA-2 family uses an identical algorithm with a variable digest size which is distinguished as SHA-224, SHA-256, SHA-384, and SHA-512.
SHA-1 is the best established of the existing SHA hash functions, and is employed in several widely used security applications and protocols. In 2005, security flaws were identified in SHA-1, namely that a possible mathematical weakness might exist, indicating that a stronger hash function would be desirable.[1] Although no attacks have yet been reported on the SHA-2 variants, they are algorithmically similar to SHA-1 and so efforts are underway to develop improved alternatives.[2][3] A new hash standard, SHA-3, is currently under development — the function will be selected via an open competition running between 2008 and 2012.
Contents |
[edit] The hash functions
[edit] SHA-0 and SHA-1
The original specification of the algorithm was published in 1993 as the Secure Hash Standard, FIPS PUB 180, by US government standards agency NIST (National Institute of Standards and Technology). This version is now often referred to as SHA-0. It was withdrawn by NSA shortly after publication and was superseded by the revised version, published in 1995 in FIPS PUB 180-1 and commonly referred to as SHA-1. SHA-1 differs from SHA-0 only by a single bitwise rotation in the message schedule of its compression function; this was done, according to NSA, to correct a flaw in the original algorithm which reduced its cryptographic security. However, NSA did not provide any further explanation or identify the flaw that was corrected. Weaknesses have subsequently been reported in both SHA-0 and SHA-1. SHA-1 appears to provide greater resistance to attacks, supporting the NSA’s assertion that the change increased the security.
SHA-1 (as well as SHA-0) produces a 160-bit digest from a message with a maximum length of (264 − 1) bits. SHA-1 is based on principles similar to those used by Ronald L. Rivest of MIT in the design of the MD4 and MD5 message digest algorithms, but has a more conservative design.
[edit] SHA-2 family
NIST published four additional hash functions in the SHA family, named after their digest lengths (in bits): SHA-224, SHA-256, SHA-384, and SHA-512. The algorithms are collectively known as SHA-2.
The algorithms were first published in 2001 in the draft FIPS PUB 180-2, at which time review and comment were accepted. FIPS PUB 180-2, which also includes SHA-1, was released as an official standard in 2002. In February 2004, a change notice was published for FIPS PUB 180-2, specifying an additional variant, SHA-224, defined to match the key length of two-key Triple DES. These variants are patented in US patent 6829355. The United States has released the patent under a royalty free license.[4]
SHA-256 and SHA-512 are novel hash functions computed with 32- and 64-bit words, respectively. They use different shift amounts and additive constants, but their structures are otherwise virtually identical, differing only in the number of rounds. SHA-224 and SHA-384 are simply truncated versions of the first two, computed with different initial values.
These hash functions are not as widely used as SHA-1, though they appear to provide much better security. This is partly because protocols like SSL do not make it easy to introduce new hash functions without breaking backwards compatibility. SHA-256 is used to authenticate Debian Linux software packages[5] and in the DKIM message signing standard; SHA-512 is part of a system to authenticate archival video from the International Criminal Tribunal of the Rwandan genocide.[6]
Currently, the best public attacks on SHA-2 break 24 of the 64 or 80 rounds.[7]
[edit] SHA-3 (in development)
An open competition for a new SHA-3 function was formally announced in the Federal Register on November 2, 2007.[8] "NIST is initiating an effort to develop one or more additional hash algorithms through a public competition, similar to the development process for the Advanced Encryption Standard (AES)."[9] Submissions were due October 31, 2008 and the proclamation of a winner and publication of the new standard are scheduled to take place in 2012.
[edit] Comparison of SHA functions
In the table below, internal state means the “internal hash sum” after each compression of a data block; see Merkle-Damgård construction for more details.
| Algorithm and variant |
Output size (bits) | Internal state size (bits) | Block size (bits) | Max message size (bits) | Word size (bits) | Rounds | Operations | Collisions found | |
|---|---|---|---|---|---|---|---|---|---|
| SHA-0 | 160 | 160 | 512 | 264 − 1 | 32 | 80 | +,and,or,xor,rot | Yes | |
| SHA-1 | 160 | 160 | 512 | 264 − 1 | 32 | 80 | +,and,or,xor,rot | None (263 attack) | |
| SHA-2 | SHA-256/224 | 256/224 | 256 | 512 | 264 − 1 | 32 | 64 | +,and,or,xor,shr,rot | None |
| SHA-512/384 | 512/384 | 512 | 1024 | 2128 − 1 | 64 | 80 | +,and,or,xor,shr,rot | None | |
[edit] Applications
SHA-1 is the most widely employed of the SHA family. It forms part of several widely used security applications and protocols, including TLS and SSL, PGP, SSH, S/MIME, and IPsec. Those applications can also use MD5; both MD5 and SHA-1 are descended from MD4. SHA-1 hashing is also used in distributed revision control systems such as Git, Mercurial, and Monotone to identify revisions, and detect data corruption or tampering.
SHA-1, SHA-224, SHA-256, SHA-384, and SHA-512 are the secure hash algorithms required by law for use in certain U. S. Government applications, including use within other cryptographic algorithms and protocols, for the protection of sensitive unclassified information. FIPS PUB 180-1 also encouraged adoption and use of SHA-1 by private and commercial organizations. SHA-1 is being retired for most government uses; the U.S. National Institute of Standards and Technology says, "Federal agencies should stop using SHA-1 for...applications that require collision resistance as soon as practical, and must use the SHA-2 family of hash functions for these applications after 2010" (emphasis in original).[10]
A prime motivation for the publication of the Secure Hash Algorithm was the Digital Signature Standard, in which it is incorporated.
The SHA hash functions have been used as the basis for the SHACAL block ciphers.
[edit] Cryptanalysis and validation
For a hash function for which L is the number of bits in the message digest, finding a message that corresponds to a given message digest can always be done using a brute force search in 2L evaluations. This is called a preimage attack and may or may not be practical depending on L and the particular computing environment. The second criterion, finding two different messages that produce the same message digest, known as a collision, requires on average only 2L/2 evaluations using a birthday attack. For the latter reason the strength of a hash function is usually compared to a symmetric cipher of half the message digest length. Thus SHA-1 was originally thought to have 80-bit strength.
Cryptographers have produced collision pairs for SHA-0 and have found algorithms that should produce SHA-1 collisions in far fewer than the originally expected 280 evaluations.
In terms of practical security, a major concern about these new attacks is that they might pave the way to more efficient ones. Whether this is the case has yet to be seen, but a migration to stronger hashes is believed to be prudent. Some of the applications that use cryptographic hashes, such as password storage, are only minimally affected by a collision attack. Constructing a password that works for a given account requires a preimage attack, as well as access to the hash of the original password (typically in the shadow file) which may or may not be trivial. Reversing password encryption (e.g. to obtain a password to try against a user's account elsewhere) is not made possible by the attacks. (However, even a secure password hash can't prevent brute-force attacks on weak passwords.)
In the case of document signing, an attacker could not simply fake a signature from an existing document—the attacker would have to produce a pair of documents, one innocuous and one damaging, and get the private key holder to sign the innocuous document. There are practical circumstances in which this is possible; until the end of 2008, it was possible to create forged SSL certificates using an MD5 collision.[11]
[edit] SHA-0
At CRYPTO 98, two French researchers, Florent Chabaud and Antoine Joux, presented an attack on SHA-0 (Chabaud and Joux, 1998): collisions can be found with complexity 261, fewer than the 280 for an ideal hash function of the same size.
In 2004, Biham and Chen found near-collisions for SHA-0—two messages that hash to nearly the same value; in this case, 142 out of the 160 bits are equal. They also found full collisions of SHA-0 reduced to 62 out of its 80 rounds.
Subsequently, on 12 August 2004, a collision for the full SHA-0 algorithm was announced by Joux, Carribault, Lemuet, and Jalby. This was done by using a generalization of the Chabaud and Joux attack. Finding the collision had complexity 251 and took about 80,000 CPU hours on a supercomputer with 256 Itanium 2 processors. (Equivalent to 13 days of full-time use of the computer.)
On 17 August 2004, at the Rump Session of CRYPTO 2004, preliminary results were announced by Wang, Feng, Lai, and Yu, about an attack on MD5, SHA-0 and other hash functions. The complexity of their attack on SHA-0 is 240, significantly better than the attack by Joux et al. [12][13]
In February 2005, an attack by Xiaoyun Wang, Yiqun Lisa Yin, and Hongbo Yu was announced which could find collisions in SHA-0 in 239 operations.[14][15]
[edit] SHA-1
In light of the results for SHA-0, some experts suggested that plans for the use of SHA-1 in new cryptosystems should be reconsidered. After the CRYPTO 2004 results were published, NIST announced that they planned to phase out the use of SHA-1 by 2010 in favor of the SHA-2 variants.[16]
In early 2005, Rijmen and Oswald published an attack on a reduced version of SHA-1—53 out of 80 rounds—which finds collisions with a computational effort of fewer than 280 operations.[17]
In February 2005, an attack by Xiaoyun Wang, Yiqun Lisa Yin, and Hongbo Yu was announced.[14] The attacks can find collisions in the full version of SHA-1, requiring fewer than 269 operations. (A brute-force search would require 280 operations.)
The authors write: "In particular, our analysis is built upon the original differential attack on SHA0 [sic], the near collision attack on SHA0, the multiblock collision techniques, as well as the message modification techniques used in the collision search attack on MD5. Breaking SHA1 would not be possible without these powerful analytical techniques."[18] The authors have presented a collision for 58-round SHA-1, found with 233 hash operations. The paper with the full attack description was published in August 2005 at the CRYPTO conference.
In an interview, Yin states that, "Roughly, we exploit the following two weaknesses: One is that the file preprocessing step is not complicated enough; another is that certain math operations in the first 20 rounds have unexpected security problems."[19]
On 17 August 2005, an improvement on the SHA-1 attack was announced on behalf of Xiaoyun Wang, Andrew Yao and Frances Yao at the CRYPTO 2005 rump session, lowering the complexity required for finding a collision in SHA-1 to 263.[20] On 18 December 2007 the details of this result were explained and verified by Martin Cochran.[21]
Christophe De Cannière and Christian Rechberger further improved the attack on SHA-1 in "Finding SHA-1 Characteristics: General Results and Applications,"[22] receiving the Best Paper Award at ASIACRYPT 2006. A two-block collision for 64-round SHA-1 was presented, found using unoptimized methods with 235 compression function evaluations.
As this attack requires the equivalent of about 235 evaluations, it is considered to be a significant theoretical break.[23] In order to find an actual collision in the full 80 rounds of the hash function, however, massive amounts of computer time would be required. To that end, a collision search for SHA-1 using the distributed computing platform BOINC is currently in progress, organized by the Graz University of Technology.[24]
At the Rump Session of CRYPTO 2006, Christian Rechberger and Christophe De Cannière claimed to have discovered a collision attack on SHA-1 that would allow an attacker to select at least parts of the message.[25][26]
[edit] Official validation
Implementations of all FIPS-approved security functions can be officially validated through the CMVP program, jointly run by the National Institute of Standards and Technology (NIST) and the Communications Security Establishment (CSE). For informal verification, a package to generate a high number of test vectors is made available for download on the NIST site; the resulting verification however does not replace in any way the formal CMVP validation, which is required by law for certain applications.
As of October 2006[update], there are more than 500 validated implementations of SHA-1, with fewer than ten of them capable of handling messages with a length in bits not a multiple of eight (see SHS Validation List). It is also important to note that some implementations available on the Internet do not digest the NIST validation vectors correctly, although they may correctly process the examples listed in the SHA-1 standard.[citation needed]
[edit] Examples and pseudocode
[edit] Example hashes
The following is an example of SHA-1 digests. ASCII encoding is assumed for all messages.
SHA1("The quick brown fox jumps over the lazy dog")
= 2fd4e1c6 7a2d28fc ed849ee1 bb76e739 1b93eb12
Even a small change in the message will, with overwhelming probability, result in a completely different hash due to the avalanche effect. For example, changing dog to cog produces a hash with different values for 81 of the 160 bits:
SHA1("The quick brown fox jumps over the lazy cog")
= de9f2c7f d25e1b3a fad3e85a 0bd17d9b 100db4b3
[edit] SHA-1 pseudocode
Pseudocode for the SHA-1 algorithm follows:
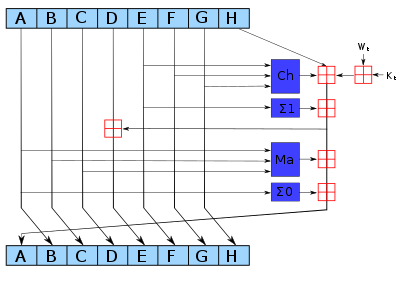
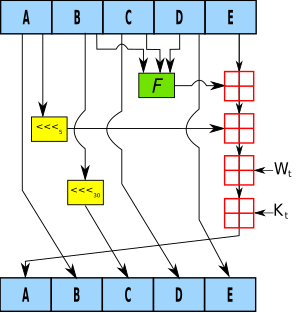
Note 1: All variables are unsigned 32 bits and wrap modulo 232 when calculating Note 2: All constants in this pseudo code are in big endian. Within each word, the most significant bit is stored in the leftmost bit position Initialize variables: h0 = 0x67452301 h1 = 0xEFCDAB89 h2 = 0x98BADCFE h3 = 0x10325476 h4 = 0xC3D2E1F0 Pre-processing: append the bit '1' to the message append k bits '0', where k is the minimum number ≥ 0 such that the resulting message length (in bits) is congruent to 448 (mod 512) append length of message (before pre-processing), in bits, as 64-bit big-endian integer Process the message in successive 512-bit chunks: break message into 512-bit chunks for each chunk break chunk into sixteen 32-bit big-endian words w[i], 0 ≤ i ≤ 15 Extend the sixteen 32-bit words into eighty 32-bit words: for i from 16 to 79 w[i] = (w[i-3] xor w[i-8] xor w[i-14] xor w[i-16]) leftrotate 1 Initialize hash value for this chunk: a = h0 b = h1 c = h2 d = h3 e = h4 Main loop: for i from 0 to 79 if 0 ≤ i ≤ 19 then f = (b and c) or ((not b) and d) k = 0x5A827999 else if 20 ≤ i ≤ 39 f = b xor c xor d k = 0x6ED9EBA1 else if 40 ≤ i ≤ 59 f = (b and c) or (b and d) or (c and d) k = 0x8F1BBCDC else if 60 ≤ i ≤ 79 f = b xor c xor d k = 0xCA62C1D6 temp = (a leftrotate 5) + f + e + k + w[i] e = d d = c c = b leftrotate 30 b = a a = temp Add this chunk's hash to result so far: h0 = h0 + a h1 = h1 + b h2 = h2 + c h3 = h3 + d h4 = h4 + e Produce the final hash value (big-endian): digest = hash = h0 append h1 append h2 append h3 append h4
Instead of the formulation from the original FIPS PUB 180-1 shown, the following equivalent expressions may be used to compute f in the main loop above:
(0 ≤ i ≤ 19): f = d xor (b and (c xor d)) (alternative 1) (0 ≤ i ≤ 19): f = (b and c) xor ((not b) and d) (alternative 2) (0 ≤ i ≤ 19): f = (b and c) + ((not b) and d) (alternative 3) (0 ≤ i ≤ 19): f = vec_sel(d, c, b) (alternative 4) (40 ≤ i ≤ 59): f = (b and c) or (d and (b or c)) (alternative 1) (40 ≤ i ≤ 59): f = (b and c) or (d and (b xor c)) (alternative 2) (40 ≤ i ≤ 59): f = (b and c) + (d and (b xor c)) (alternative 3) (40 ≤ i ≤ 59): f = (b and c) xor (b and d) xor (c and d) (alternative 4)
[edit] SHA-256 (a SHA-2 variant) pseudocode
Pseudocode for the SHA-256 algorithm follows. Note the great increase in mixing between bits of the w[16..63] words compared to SHA-1.
Note 1: All variables are unsigned 32 bits and wrap modulo 232 when calculating Note 2: All constants in this pseudo code are in big endian Initialize variables (first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19): h0 := 0x6a09e667 h1 := 0xbb67ae85 h2 := 0x3c6ef372 h3 := 0xa54ff53a h4 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19 Initialize table of round constants (first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..311): k[0..63] := 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2 Pre-processing: append the bit '1' to the message append k bits '0', where k is the minimum number >= 0 such that the resulting message length (in bits) is congruent to 448 (mod 512) append length of message (before pre-processing), in bits, as 64-bit big-endian integer Process the message in successive 512-bit chunks: break message into 512-bit chunks for each chunk break chunk into sixteen 32-bit big-endian words w[0..15] Extend the sixteen 32-bit words into sixty-four 32-bit words: for i from 16 to 63 s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3) s1 := (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor (w[i-2] rightshift 10) w[i] := w[i-16] + s0 + w[i-7] + s1 Initialize hash value for this chunk: a := h0 b := h1 c := h2 d := h3 e := h4 f := h5 g := h6 h := h7 Main loop: for i from 0 to 63 s0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22) maj := (a and b) xor (a and c) xor (b and c) t2 := s0 + maj s1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25) ch := (e and f) xor ((not e) and g) t1 := h + s1 + ch + k[i] + w[i] h := g g := f f := e e := d + t1 d := c c := b b := a a := t1 + t2 Add this chunk's hash to result so far: h0 := h0 + a h1 := h1 + b h2 := h2 + c h3 := h3 + d h4 := h4 + e h5 := h5 + f h6 := h6 + g h7 := h7 + h Produce the final hash value (big-endian): digest = hash = h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
The ch and maj functions can be optimized the same way as described for SHA-1.
SHA-224 is identical to SHA-256, except that:
- the initial variable values
h0throughh7are different, and - the output is constructed by omitting
h7.
Here the initial values for the variables (in big endian):
h0 := 0xc1059ed8
h1 := 0x367cd507
h2 := 0x3070dd17
h3 := 0xf70e5939
h4 := 0xffc00b31
h5 := 0x68581511
h6 := 0x64f98fa7
h7 := 0xbefa4fa4
SHA-512 is identical in structure, but:
- all numbers are 64 bits long,
- there are 80 rounds instead of 64,
- the initial values and additive constants are extended to 64 bits, and
- the shift and rotate amounts used are different.
SHA-384 is identical to SHA-512, except that:
- the initial values
h0throughh7are different, and - the output is constructed by omitting
h6andh7.
[edit] See also
- sha1sum
- Digital timestamping
- Hash collision
- Hashcash
- RIPEMD-160 (Patent free)
- Secure Hash Standard
- Tiger
- WHIRLPOOL (Patent free)
[edit] References
- ^ Schneier on Security: Cryptanalysis of SHA-1
- ^ Schneier on Security: NIST Hash Workshop Liveblogging (5)
- ^ Hash cracked - heise Security
- ^ Licensing Declaration for US patent 6829355.. https://datatracker.ietf.org/ipr/858/. Retrieved on 2008-02-17.
- ^ Debian codebase in Google Code
- ^ John Markoff, A Tool to Verify Digital Records, Even as Technology Shifts, New York Times, January 26, 2009
- ^ Somitra Kumar Sanadhya and Palash Sarkar, New Collision attacks Against Up To 24-step SHA-2
- ^ http://csrc.nist.gov/groups/ST/hash/documents/FR_Notice_Nov07.pdf
- ^ Bounce to index.html
- ^ National Institute on Standards and Technology Computer Security Resource Center, NIST'S POLICY ON HASH FUNCTIONS, accessed March 29, 2009.
- ^ Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger, MD5 considered harmful today: Creating a rogue CA certificate, accessed March 29, 2009
- ^ Freedom to Tinker » Blog Archive » Report from Crypto 2004
- ^ http://groups.google.com/groups?selm=fgrieu-05A994.05060218082004%40individual.net
- ^ a b Schneier on Security: SHA-1 Broken
- ^ http://www.infosec.sdu.edu.cn/paper/sha0-crypto-author-new.pdf
- ^ http://csrc.nist.gov/hash_standards_comments.pdf
- ^ Cryptology ePrint Archive
- ^ http://theory.csail.mit.edu/~yiqun/shanote.pdf
- ^ Fixing a hole in security | Tech News on ZDNet
- ^ Schneier on Security: New Cryptanalytic Results Against SHA-1
- ^ Cryptology ePrint Archive
- ^ SpringerLink Home - Main
- ^ IAIK Krypto Group - Description of SHA-1 Collision Search Project
- ^ SHA-1 Collision Search Graz
- ^ SHA-1 hash function under pressure - heise Security
- ^ Crypto 2006 Rump Schedule
- Florent Chabaud, Antoine Joux: Differential Collisions in SHA-0. CRYPTO 1998. pp56–71
- Eli Biham, Rafi Chen, Near-Collisions of SHA-0, Cryptology ePrint Archive, Report 2004/146, 2004 (appeared on CRYPTO 2004) [1]
- Xiaoyun Wang, Hongbo Yu and Yiqun Lisa Yin, Efficient Collision Search Attacks on SHA-0, CRYPTO 2005 [2]
- Xiaoyun Wang, Yiqun Lisa Yin and Hongbo Yu, Finding Collisions in the Full SHA-1, CRYPTO 2005 [3]
- Henri Gilbert, Helena Handschuh: Security Analysis of SHA-256 and Sisters. Selected Areas in Cryptography 2003: pp175–193
- "Proposed Revision of Federal Information Processing Standard (FIPS) 180, Secure Hash Standard". Federal Register 59 (131): 35317–35318. 1994-07-11. http://frwebgate1.access.gpo.gov/cgi-bin/waisgate.cgi?WAISdocID=5963452267+0+0+0&WAISaction=retrieve. Retrieved on 2007-04-26.
[edit] External links
[edit] Online Hash Calculators
- Hash'em all! – free online text and file hashing with over 30 different algorithms
- sha1-lookup.com – SHA-1 reverse lookup database
- hash-it.net – instant javascript based text hashing with three algorithms
[edit] Standards: SHA-0, SHA-1, SHA-2, SHA-3...
- Specifications for a Secure Hash Standard (SHS) – Draft for proposed SHS standard (SHA-0)
- Secure Hash Standard (SHS) – Proposed SHS standard (SHA-0)
- CSRC Cryptographic Toolkit – Official NIST site for the Secure Hash Standard
- FIPS 180-2: Secure Hash Standard (SHS) (PDF, 236 kB) – Current version of the Secure Hash Standard (SHA-1, SHA-224, SHA-256, SHA-384, and SHA-512), 1 August 2002, amended 25 February 2004
- NIST Cryptographic Hash Project SHA-3 competition
- RFC 3174 (with sample C implementation)
[edit] Cryptanalysis
- Interview with Yiqun Lisa Yin concerning the attack on SHA-1
- Lenstra's Summary of impact of the February 2005 cryptanalytic results
- Explanation of the successful attacks on SHA-1 (3 pages, 2006)
- Cryptography Research - Hash Collision Q&A
[edit] Implementations
- The OpenSSL Project – The widely used OpenSSL
cryptolibrary includes free, open-source implementations of SHA-1, SHA-224, SHA-256, SHA-384, and SHA-512 - Crypto++ Crypto++ Library is a free C++ class library of cryptographic schemes.
- Bouncy Castle The Bouncy Castle Library is a free Java and C# class library that contains implementations of the SHA-1, SHA-224, SHA-256, SHA-384 and SHA-512 algorithms as well as other algorithms like Whirlpool, Tiger, RIPEMD, GOST-3411, MD2, MD4 and MD5.
|
|||||||||||||||||||||||||||||||||||