Surreal number
From Wikipedia, the free encyclopedia
| This article may be too long to comfortably read and navigate. Please consider splitting content into sub-articles and using this article for a summary of the key points of the subject. |
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number. The surreals share many properties with the reals, including a total order ≤ and the usual arithmetic operations (addition, subtraction, multiplication, and division); as such, they form an ordered Field.[1] In a rigorous set theoretic sense, the surreal numbers are the largest possible ordered field; all other ordered fields, such as the rationals, the reals, the rational functions, the Levi-Civita field, the superreal numbers, and the hyperreal numbers, are subfields of the surreals. The surreals also contain all transfinite ordinal numbers reachable in the set theory in which they are constructed.
The definition and construction of the surreals is due to John Horton Conway. They were introduced in Donald Knuth's 1974 book Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. This book is a mathematical novelette, and is notable as one of the rare cases where a new mathematical idea was first presented in a work of fiction. In his book, which takes the form of a dialogue, Knuth coined the term surreal numbers for what Conway had simply called numbers originally. Conway liked the new name, and later adopted it himself. Conway then described the surreal numbers and used them for analyzing games in his 1976 book On Numbers and Games.
Contents |
[edit] Constructing surreal numbers
A form is a pair of sets, called its left set L and its right set R; it is written { L | R }. (When L and R are given as lists of elements, the braces around them can be omitted.) If there is no combination of x in L and y in R such that x≥y, the form is numeric. Either or both of L and R may be the empty set; without knowing anything about the potential elements of L and R, or about the comparison operation ≥, one can exhibit the numeric form { { } | { } }, also written { | }.
Construction Rule
- A form { L | R } is numeric if and only if there is no combination of
 and
and  such that xR ≤ xL.
such that xR ≤ xL.
The numeric forms are placed in equivalence classes; each such equivalence class is a surreal number. The equivalence class containing { | } is labeled 0; in other words, { | } is a form of the surreal number 0. The elements of L and R are drawn from the universe of the surreal numbers (not of forms, but of their equivalence classes). The recursive definition of surreal numbers is completed by defining comparison and equivalence:
Comparison Rule
- Given numeric forms x = { XL | XR } and y = { YL | YR }, x ≤ y if and only if:
- there is no
 such that y ≤ xL, and
such that y ≤ xL, and - there is no
 such that yR ≤ x.
such that yR ≤ x.
- there is no
- A comparison y ≤ c between a form y and a surreal number c is performed by choosing a form z from the equivalence class c and evaluating y ≤ z; and likewise for c ≤ x and for comparison b ≤ c between two surreal numbers.
A ordering relationship must have the property that x = y (i. e., x ≤ y and y ≤ x are both true) only when x and y are the same object. This is not the case for surreal number forms, but is true by construction for surreal numbers.
Equivalence Rule
- Two surreal number forms x and y are forms of the same number (lie in the same equivalence class) if and only if both x ≤ y and y ≤ x.
This group of definitions is recursive, and requires some form of mathematical induction to define the universe of objects (forms and numbers) that occur in them. The only surreal numbers reachable via finite induction are the dyadic fractions; a wider universe is reachable given some form of transfinite induction.
Induction Rule
- There is a generation S0 = { 0 }, in which 0 consists of the single form { | }.
- Given any ordinal number n, the generation Sn is the set of all surreal numbers that are generated by the construction rule from subsets of
 .
.
The base case is actually a special case of the induction rule, with 0 taken as a label for the "least ordinal". Since there exists no Si with i < 0, the expression  is the empty set; the only subset of the empty set is the empty set, and therefore S0 consists of a single surreal form { | } lying in a single equivalence class 0.
is the empty set; the only subset of the empty set is the empty set, and therefore S0 consists of a single surreal form { | } lying in a single equivalence class 0.
The first iteration of the induction rule produces the three numeric forms { | 0 } < { | } < { 0 | } (the form { 0 | 0 } is non-numeric because 0≤0). The equivalence class containing { 0 | } is labeled 1 and the equivalence class containing { | 0 } is labeled −1. These three labels have a special significance in the axioms that define a ring; they are the additive identity (0), the multiplicative identity (1), and the additive inverse of 1 (−1). The arithmetic operations defined below are consistent with these labels.
For every i < n, since every valid form in Si is also a valid form in Sn, all of the numbers in Si also appear in Sn (as supersets of their representation in Si). (The set union expression appears in our construction rule, rather than the simpler form Sn-1, so that the definition also makes sense when n is a limit ordinal.) Numbers in Sn that are a superset of some number in Si are said to have been inherited from generation i. The smallest value of α for which a given surreal number appears in Sα is called its birthday. For example, the birthday of 0 is 0, and the birthday of −1 is 1.
A second iteration of the construction rule yields the following ordering of equivalence classes:
- { | −1 } = { | −1, 0 } = { | −1, 1 } = { | −1, 0, 1 }
- < { | 0 } = { | 0, 1 }
- < { −1 | 0 } = { −1 | 0, 1 }
- < { | } = { −1 | } = { | 1 } = { −1 | 1 }
- < { 0 | 1 } = { −1, 0 | 1 }
- < { 0 | } = { −1, 0 | }
- < { 1 | } = { 0, 1 | } = { −1, 1 | } = { −1, 0, 1 | }
Comparison of these equivalence classes is consistent irrespective of the choice of form. Three observations follow:
- S2 contains four new surreal numbers. Two contain extremal forms: { | −1, 0, 1 } contains all numbers from previous generations in its right set, and { −1, 0, 1 | } contains all numbers from previous generations in its left set. The others have a form that partitions all numbers from previous generations into two non-empty sets.
- Every surreal number x that existed in the previous "generation" exists also in this generation, and includes at least one new form: a partition of all numbers other than x from previous generations into a left set (all numbers less than x) and a right set (all numbers greater than x).
- The equivalence class of a number depends only on the maximal element of its left set and the minimal element of the right set.
The informal interpretations of { 1 | } and { | −1 } are "the number just after 1" and "the number just before −1" respectively; their equivalence classes are labeled 2 and −2. The informal interpretations of { 0 | 1 } and { −1 | 0 } are "the number halfway between 0 and 1" and "the number halfway between −1 and 0" respectively; their equivalence classes are labeled 1/2 and −1/2. These labels will also be justified by the rules for surreal addition and multiplication below.
The equivalence classes at each stage n of induction may be characterized by their n-complete forms (each containing as many elements as possible of previous generations in its left and right sets). Either this complete form contains every number from previous generations in its left or right set, in which case this is the first generation in which this number occurs; or it contains all numbers from previous generations but one, in which case it is a new form of this one number. We retain the labels from the previous generation for these "old" numbers, and write the ordering above using the old and new labels:
- −2 < −1 < −1/2 < 0 < 1/2 < 1 < 2.
The third observation extends to all surreal numbers with finite left and right sets. (For infinite left or right sets, this is valid in an altered form, since infinite sets might not contain a maximal or minimal element.) The number { 1, 2 | 5, 8 } is therefore equivalent to { 2 | 5 }; one can establish that these are forms of 3 by using the birthday property, which is a consequence of the rules above.
Birthday property
- A form x occurring in generation n lies in a number inherited from an earlier generation i < n if and only if there is some number in Si that is greater than all elements of the left set of x and less than all elements of the right set of x. If x is inherited from any generation earlier than n, there is a least such i, and exactly one number c with this least birthday i lies between the left and right sets of x. x is a form of this c, i. e., it lies in the equivalence class in Sn that is a superset of the representation of c in generation i.
[edit] Surreal arithmetic
The addition, negation (additive inverse), and multiplication of surreal number forms x = { XL | XR } and y = { YL | YR } are defined by three recursive formulas. Negation is simplest:
Negation
 ,
,- where
 .
.
This formula involves the negation of the surreal numbers appearing in the left and right sets of x, which is to be understood as the result of choosing a form of the number, evaluating the negation of this form, and taking the equivalence class of the resulting form. This only makes sense if the result is the same irrespective of the choice of form of the operand. This can be proven inductively using the fact that the numbers occurring in XL and XR are drawn from generations earlier than that in which the form x first occurs, and observing the special case:
- -0 = - { | } = { | } = 0.
The definition of addition is also a recursive formula:
Addition
 ,
,- where
 .
.
This formula involves sums of one of the original operands and a surreal number drawn from the left or right set of the other. These are to be understood as the result of choosing a form of the numeric operand, performing the sum of the two forms, and taking the equivalence class of the resulting form. This only makes sense if the result is the same irrespective of the choice of form of the numeric operand. This can also be proven inductively with the special cases:
- 0 + 0 = { | } + { | } = { | } = 0
- x + 0 = x + { | } = { XL + 0 | XR + 0 } = { XL | XR } = x
- 0 + y = { | } + y = { 0 + YL | 0 + YR } = { YL | YR } = y
(The latter two cases are of course themselves proven inductively.)
The recursive formula for multiplication contains arithmetic expressions involving the operands and their left and right sets, such as the expression XRy + xYR − XRYR that appears in the left set of the product of x and y. This is to be understood as the set of surreal numbers resulting from choosing one number from each set that appears in the expression and evaluating the expression on these numbers. (In each individual evaluation of the expression, only one number is chosen from each set, and is substituted in each place where that set appears in the expression.)
This depends, in turn, on the ability to (a) multiply pairs of surreal numbers drawn from the left and right sets of x and y to get a surreal number, and negate the result; (b) multiply the surreal number form x or y and a surreal number drawn from the left or right set of the other operand to get a surreal number; and (c) add the resulting surreal numbers. This again involves special cases, this time containing 0 = { | }, the multiplicative identity 1 = { 0 | }, and its additive inverse -1 = { | 0 }.
Multiplication
It can be shown that these formulas are consistent, in the sense that:
- addition and negation are defined recursively in terms of "simpler" addition and negation steps, so that operations on numbers with birthday n will eventually be expressed entirely in terms of operations on numbers with birthdays less than n;
- multiplication is defined recursively in terms of additions, negations, and "simpler" multiplication steps, so that the product of numbers with birthday n will eventually be expressed entirely in terms of sums and differences of products of numbers with birthdays less than n;
- as long as the operands are well-defined surreal number forms (each element of the left set is less than each element of the right set), the results are again well-defined surreal number forms;
- when forms are gathered into equivalence classes using the "birthday rule", the result of negating x or adding or multiplying x and y does not depend on the choice of form of x and y; and
- these operations obey the associativity, commutativity, additive inverse, and distributivity axioms in the definition of a field, with additive identity 0 = { | } and multiplicative identity 1 = { 0 | }.
With these rules one can now verify that the numbers found in the first few generations were properly labeled. The construction rule is repeated to obtain more generations of surreals:
- S0 = { 0 }
- S1 = { −1 < 0 < 1 }
- S2 = { −2 < −1 < −1/2 < 0 < 1/2 < 1 < 2}
- S3 = { −3 < −2 < −3/2 < −1 < −3/4 < −1/2 < −1/4 < 0 < 1/4 < 1/2 < 3/4 < 1 < 3/2 < 2 < 3 }
- S4 = { -4 < −3 < ... < -1/8 < 0 < 1/8 < 1/4 < 3/8 < 1/2 < 5/8 < 3/4 < 7/8 < 1 < 5/4 < 3/2 < 7/4 < 2 < 5/2 < 3 < 4 }
For each natural number (finite ordinal) n, all numbers generated in Sn are dyadic fractions, i.e., can be written as an irreducible fraction  where a and b are integers and 0 ≤ b < n.
where a and b are integers and 0 ≤ b < n.
The class of all surreal numbers that are generated in some Sn for finite n may be denoted as S* =  . Since every Sn is well-ordered, so is S*; in particular, one may form the three classes S0 = { 0 }, S+ =
. Since every Sn is well-ordered, so is S*; in particular, one may form the three classes S0 = { 0 }, S+ =  , and S- =
, and S- =  , and state that S* is the union of these three classes. No individual Sn is closed under addition and multiplication (except S0), but S* is; it is the subring of the rationals consisting of all dyadic fractions.
, and state that S* is the union of these three classes. No individual Sn is closed under addition and multiplication (except S0), but S* is; it is the subring of the rationals consisting of all dyadic fractions.
At an appropriate stage of transfinite induction, the surreal numbers may be expected to form a category on which the addition and multiplication operations (as well as the surreal construction step) are closed, and in which the multiplicative inverse of every nonzero number can be found. Assuming that one can find such a class, the surreal numbers, with their ordering and these algebraic operations, constitute an ordered field, with the caveat that they do not form a set but a proper class. In fact, it is a very special ordered field: the biggest one. Every other ordered field can be embedded in the surreals. (See also the definition of rational numbers and real numbers.)
[edit] "To Infinity ..."
Let there be an ordinal ω greater than the natural numbers, and define Sω as the set of all surreal numbers generated by the construction rule from subsets of S*. (This is the same inductive step as before, since the ordinal number ω is the smallest ordinal that is larger than all natural numbers; however, the set union appearing in the inductive step is now an infinite union of finite sets, and so this step can only be performed in a set theory that allows such a union.) A unique infinitely large positive number occurs in Sω:
Sω also contains objects that can be identified as the rational numbers. For example, the ω-complete form of the fraction 1/3 is given by:
 .
.
The product of this form of 1/3 with any form of 3 is a form whose left set contains only numbers less than 1 and whose right set contains only numbers greater than 1; the birthday property implies that this product is a form of 1.
Not only do all the rest of the rational numbers appear in Sω; the remaining finite real numbers do too. For example
 .
.
The only infinities in Sω are ω and -ω; but there are other non-real numbers in Sω among the reals. Consider the smallest positive number in Sω:
 .
.
This number is larger than zero but less than all positive dyadic fractions. It is therefore an infinitesimal number, often labeled ε. The only infinitesimals in Sω are ε and its opposite -ε. The ω-complete forms of ε (resp. -ε) is the same as differ the ω-complete form of 0 except that 0 is included in the left (resp. right) set.
For every dyadic fraction x in S*, x+ε and x-ε are infinitely good approximations of x. By definition
 .
. .
.
So that x+ε and x-ε are indeed the best approximation of x above and below.
One can determine the relationship between ω and ε by multiplying them to obtain:
- ω · ε = { ε · S+ | ω · S+ + S* + ε · S* }.
This expression is only well-defined in a set theory which permits transfinite induction up to  . In such a system, one can demonstrate that all the elements of the left set of ω · ε are positive infinitesimals and all the elements of the right set are positive infinities, and therefore ω · ε is the oldest positive finite number, i. e., 1. Consequently,
. In such a system, one can demonstrate that all the elements of the left set of ω · ε are positive infinitesimals and all the elements of the right set are positive infinities, and therefore ω · ε is the oldest positive finite number, i. e., 1. Consequently,
- 1/ε = ω.
Some authors systematically use ω−1 in place of the symbol ε.
Contents of Sω Given any x = { L | R } in Sω, we are in one of the following case:
- L and R are both empty, in which case x = 0;
- R is empty and some integer n≥0 is greater than every element of L, in which case x equals the smallest of such integer n;
- R is empty and no integer n is greater than every element of L, in which case x equals +ω;
- L is empty and some integer n≤0 is less than every element of R, in which case x equals the largest such integer n;
- L is empty and no integer n is less than every element of R, in which case x equals -ω;
- L and R are both non-empty, and:
- some dyadic fraction y is "strictly between" L and R (greater than all elements of L and less than all elements of R), in which case x equals the oldest such dyadic fraction y;
- no dyadic fraction y lies strictly between L and R, but some dyadic fraction
 is greater than or equal to all elements of L and less than all elements of R, in which case x equals y+ε;
is greater than or equal to all elements of L and less than all elements of R, in which case x equals y+ε; - no dyadic fraction y lies strictly between L and R, but some dyadic fraction
 is greater than all elements of L and less than or equal to all elements of R, in which case x equals y-ε;
is greater than all elements of L and less than or equal to all elements of R, in which case x equals y-ε; - every dyadic fraction is either greater than some element of R or less than some element of L, in which case x is some real number that has no representation as a dyadic fraction.
Because every real number can be approximated by a dyadic fraction, we get all the real numbers. In addition, Sω contains two infinites ω and -ω, as well as their (multiplicative) inverse, the infinitesimals ε and -ε.
Note however that Sω is not an algebric field as ω2=ω ω={ω|}, is in Sω2, but not in Sω.
This construction of the real numbers differs from the Dedekind cuts of standard analysis in that it starts from dyadic fractions rather than general rationals and naturally identifies each dyadic fraction in Sω with its forms in previous generations. The rationals are not an identifiable stage in the the surreal construction; they are merely the subset Q of Sω containing all elements x such that x b = a for some a and some nonzero b, both drawn from S*. By demonstrating that Q is closed under individual repetitions of the surreal arithmetic operations, one can show that it is a field; and by showing that every element of Q is reachable from S* by a finite series (no more than two, actually) of arithmetic operations including multiplicative inversion, one can show that Q is strictly smaller than the subset of Sω identified with the reals.
[edit] "... and Beyond."
Continuing to perform transfinite induction beyond Sω produces more ordinal numbers α, each represented as the largest surreal number having birthday α. (This is essentially a definition of the ordinal numbers resulting from transfinite induction.) The first such ordinal is ω+1 = { ω | }. There is another positive infinite number in generation ω+1:
- ω−1 = { 1, 2, 3, 4, ... | ω }.
It is important to observe that the surreal number ω−1 is not an ordinal; the ordinal ω is not the successor of any ordinal. This is a surreal number with birthday ω+1, which is labeled ω−1 on the basis that it coincides with the sum of ω = { 1, 2, 3, 4, ... | } and −1 = { | 0 }. Similarly, there are two new infinitesimal numbers in generation ω+1:
- 2ε = ε + ε = { ε | 1+ε, 1/2+ε, 1/4+ε, 1/8+ε, ... } and
- ε/2 = ε · 1/2 = { 0 | ε }.
At a later stage of transfinite induction, there is a number larger than ω+k for all natural numbers k:
- 2ω = ω + ω = { ω+1, ω+2, ω+3, ω+4, ... | }
This number may be labeled ω + ω both because its birthday is ω + ω (the first ordinal number not reachable from ω by the successor operation) and because it coincides with the surreal sum of ω and ω; it may also be labeled 2ω because it coincides with the product of ω = { 1, 2, 3, 4, ... | } and 2 = { 1 | }. It is the second limit ordinal; reaching it from ω via the construction step requires a transfinite induction on  . This involves an infinite union of infinite sets, which is a "stronger" set theoretic operation than the previous transfinite induction required.
. This involves an infinite union of infinite sets, which is a "stronger" set theoretic operation than the previous transfinite induction required.
Note that the conventional addition and multiplication of ordinals does not always coincide with these operations on their surreal representations. The sum of ordinals 1 + ω equals ω, but the surreal sum is commutative and produces 1 + ω = ω + 1 > ω. The addition and multiplication of the surreal numbers associated with ordinals coincides with the natural sum and natural product of ordinals.
Just as 2ω is bigger than ω+n for any natural number n, there is a surreal number ω/2 that is infinite but smaller than ω−n for any natural number n.
- ω/2 = { S* | ω − S* }
where x − Y = { x − y | y in Y }. It can be identified as the product of ω and the form { 0 | 1 } of 1/2. The birthday of ω/2 is the limit ordinal 2ω.
Labels for the surreal numbers that arise in later stages of transfinite induction are determined by reference to the rules of ordinal arithmetic and of surreal exponentiation.
Base 2 Exponentiation
- The base 2 exponential of a surreal number x, denoted 2x, is defined as follows:
- 20 = { 0 | } = 1; 21 = { 0, 1 | } = 2; 2−1 = { 0 | 1 } = 1/2.
- 2x+y = 2x · 2y. This leads to implicit definitions for exponentials of negative and dyadic fractional surreals:
- 2−x = (2x)−1 (where (y)−1 is the unique solution z of y·z=1 restricted to y,z > 0).
 (where
(where  is the unique solution z of z·z=y restricted to y,z > 0).
is the unique solution z of z·z=y restricted to y,z > 0).
- The existence and uniqueness of these solutions is challenging to prove, and provides the connection between the surreal number construction and the real-closed fields of model theory.
- When the birthday α of the exponent x is a limit ordinal, the value of 2x is determined by reference to its α-complete form, and is computed differently depending on whether the left set or right set of this form has an extremal member. (They cannot both have extremal members; if they did, some number with birthday < α would lie between them. It is possible for neither the left set nor the right set to have an extremal member, as in the case where α=ω and x is an irrational number.)
- If the right set of the α-complete form of x has a least member x0, then
 . (The value of
. (The value of  can be determined, since x0 has an earlier birthday.) The quantity z=x0−x is a positive infinitesimal; its exponetial 2−z is calculated by using its Taylor series, which alternates between negative and positive terms. Multiply
can be determined, since x0 has an earlier birthday.) The quantity z=x0−x is a positive infinitesimal; its exponetial 2−z is calculated by using its Taylor series, which alternates between negative and positive terms. Multiply  by 2−z to get 2x.
by 2−z to get 2x. - If the left set of the α-complete form of x has a greatest member x0, then
 . This time z=x−x0 is a positive infinitesimal; multiply
. This time z=x−x0 is a positive infinitesimal; multiply  by the multiplicative inverse of 2−z to get 2x.
by the multiplicative inverse of 2−z to get 2x. - If neither the left set nor the right set of the α-complete form of x has an extremal member, then
 for any form { XL | XR } of x. (This formula applies to the case where x is the limit ordinal α or its negation, as well as to numbers resulting from "Conway cuts".)
for any form { XL | XR } of x. (This formula applies to the case where x is the limit ordinal α or its negation, as well as to numbers resulting from "Conway cuts".)
- If the right set of the α-complete form of x has a least member x0, then
The use of the Taylor series of 2−z = exp(−(ln 2)·z) ensures that 2ε · 2−ε = 1 and so forth. The definition is phrased in terms of 2−z for positive infinitesimal z only because it results in a Taylor series whose terms alternate between positive and negative (and are of strictly decreasing magnitude because zk+1 < czk for all real c). Truncating the series at order zk always produces an overestimate for even k and an underestimate for odd k. This results in a direct construction of left and right sets of the "limit" of the series, without use of deep results about limits and convergence.
The exponential map x → 2x is of great interest in proving facts about the surreals. It has the fixed point ω; this is its only fixed point among numbers with birthday less than ε0 (epsilon nought). If one starts from the first ordinal greater than ω and applies the exponential map repeatedly, one obtains a series of larger ordinals:
- ω+1 → ω·2 → ω2 → ωω →
 → ... →
→ ... → 
(see Knuth's up-arrow notation). Starting instead from the non-ordinal ω−1, one obtains a similar pattern of exponentiation for infinite non-ordinals:
- ω−1 → ω·1/2 →
 ( → ωε →
( → ωε →  ) →
) →  →
→  → ...
→ ...
Each step of this sequence produces the smallest infinite number whose birthday is the ordinal in the same step of the previous sequence, with the exception of the two steps in parentheses; they are the smallest infinite numbers in generations ω3 and ω4 respectively.
In a sufficiently strong axiomatization of set theory, one can form generations of surreals labeled by a countable series of countable ordinals:
 ,
,  ,
,  ,
,  , ...
, ...
Other fields of interest occur as subsets of these generations; for instance, the rational expressions in ω, which form a classical example of a non-Archimedean field, occur as a subset of generation ωω, much as the rational numbers occur as a subset of generation ω. But for every k≥2, generation  contains infinitesimal elements much smaller than the multiplicative inverse of its ordinal. Consequently, terminating transfinite induction before any particular
contains infinitesimal elements much smaller than the multiplicative inverse of its ordinal. Consequently, terminating transfinite induction before any particular  results in a ring that is also closed under the construction step, but not in a field.
results in a ring that is also closed under the construction step, but not in a field.
However, the countable union of the sets  for natural numbers k, which may be denoted
for natural numbers k, which may be denoted  , is closed under both the surreal construction step and the arithmetic operations, including the multiplicative inverse. (The existence of the multiplicative inverse of any nonzero number in Σ is provable using the fact that the base 2 exponential maps Σ invertibly onto its positive half Σ+. This results in the formula
, is closed under both the surreal construction step and the arithmetic operations, including the multiplicative inverse. (The existence of the multiplicative inverse of any nonzero number in Σ is provable using the fact that the base 2 exponential maps Σ invertibly onto its positive half Σ+. This results in the formula  , in which the positive quantity chosen for inversion is | x | 2 for ease of extension to the surcomplex numbers.) This set is the smallest possible complete field of surreals—a set that is both complete in the sense of the surreal construction step and closed under the defining operations of a field. It has order type ε0 (epsilon nought), which may also be denoted
, in which the positive quantity chosen for inversion is | x | 2 for ease of extension to the surcomplex numbers.) This set is the smallest possible complete field of surreals—a set that is both complete in the sense of the surreal construction step and closed under the defining operations of a field. It has order type ε0 (epsilon nought), which may also be denoted  .
.
If one were to go beyond  , many more numbers could be generated via transfinite induction; in fact so many that no set can hold them all. In a large enough universe, the surreal numbers, like the ordinal numbers, form a proper class, instead of a set.
, many more numbers could be generated via transfinite induction; in fact so many that no set can hold them all. In a large enough universe, the surreal numbers, like the ordinal numbers, form a proper class, instead of a set.
[edit] Powers of ω
To classify the "orders" of infinite surreal numbers, also known as archimedean classes, Conway associated to each surreal number x the surreal number
- ωx = { 0, r ωxL | s ωxR },
where r and s range over the positive real numbers. If 0 ≤ x < y then ωy is "infinitely greater" than ωx, in that it is greater than r ωx for all real numbers r. Powers of ω also satisfy the conditions
- ωx ωy = ωx+y,
- ω−x = 1/ωx,
so they behave the way one would expect powers to behave.
Each power of ω also has the redeeming feature of being the simplest surreal number in its archimedean class; conversely, every archimedean class within the surreal numbers contains a unique simplest member. Thus, for every positive surreal number x there will always exist some positive real number r and some surreal number y so that x − r ωy is "infinitely smaller" than x. This gets extended by transfinite induction so that every surreal number x has a "normal form" analogous to the Cantor normal form for ordinal numbers. Every surreal number may be uniquely written as
- x = r0 ωy0 + r1 ωy1 + …,
where every rα is a nonzero real number and the yαs form a strictly decreasing sequence of surreal numbers. This "sum", however, may have infinitely many terms, and in general has the length of an arbitrary ordinal number.
Looked at in this manner, the surreal numbers resemble a power series field, except that the decreasing sequences of exponents must be bounded in length by an ordinal and are not allowed to be as long as the class of ordinals.
[edit] Games
The definition of surreal numbers contained one restriction: each element of L must be strictly less than each element of R. If this restriction is dropped we can generate a more general class known as games. All games are constructed according to this rule:
- Construction Rule
If L and R are two sets of games then { L | R } is a game.
Addition, negation, multiplication, and comparison are all defined the same way for both surreal numbers and games.
Every surreal number is a game, but not all games are surreal numbers, e.g. the game { 0 | 0 } is not a surreal number. The class of games is more general than the surreals, and has a simpler definition, but lacks some of the nicer properties of surreal numbers. The class of surreal numbers forms a field, but the class of games does not. The surreals have a total order: given any two surreals, they are either equal, or one is greater than the other. The games have only a partial order: there exist pairs of games that are neither equal, greater than, nor less than each other. Each surreal number is either positive, negative, or zero. Each game is either positive, negative, zero, or fuzzy (incomparable with zero, such as {1|−1}).
A move in a game involves the player whose move it is choosing a game from those available in L (for the left player) or R (for the right player) and then passing this chosen game to the other player. A player who cannot move because the choice is from the empty set has lost. A positive game represents a win for the left player, a negative game for the right player, a zero game for the second player to move, and a fuzzy game for the first player to move.
If x, y, and z are surreals, and x=y, then x z=y z. However, if x, y, and z are games, and x=y, then it is not always true that x z=y z. Note that "=" here means equality, not identity.
[edit] Surreal numbers and combinatorial game theory
The surreal numbers were originally motivated by studies of the game Go,[2] and there are numerous connections between popular games and the surreals. In this section, we will use a capitalized Game for the mathematical object {L|R}, and the lowercase game for recreational games like Chess or Go.
We consider games with these properties:
- Two players (named Left and Right)
- Deterministic (the game at each step will completely depend on the choices the players make, rather than a random factor)
- No hidden information (such as cards or tiles that a player hides)
- Players alternate taking turns (the game may or may not allow multiple moves in a turn)
- Every game must end in a finite number of moves
- As soon as there are no legal moves left for a player, the game ends, and that player loses
For most games, the initial board position gives no great advantage to either player. As the game progresses and one player starts to win, board positions will occur where that player has a clear advantage. For analyzing games, it is useful to associate a Game with every board position. The value of a given position will be the Game {L|R}, where L is the set of values of all the positions that can be reached in a single move by Left. Similarly, R is the set of values of all the positions that can be reached in a single move by Right.
The zero Game (called 0) is the Game where L and R are both empty, so the player to move next (L or R) immediately loses. The sum of two Games G = { L1 | R1 } and H = { L2 | R2 } is defined as the Game G + H = { L1 + L2 | R1 + R2 } where the player to move chooses which of the Games to play in at each stage, and the loser is still the player who ends up with no legal move. One can imagine two chess boards between two players, with players making moves alternatively, but with complete freedom as to which board to play on. If G is the Game {L | R}, -G is the game {-R | -L}, i.e. with the role of the two players reversed. It is easy to show G - G = 0 for all Games G (where G - H is defined as G + (-H)).
This simple way to associate Games with games yields a very interesting result. Suppose two perfect players play a game starting with a given position whose associated Game is x. We can classify all Games into 4 classes as as follows:
- If x > 0 then Left will win, regardless of who plays first.
- If x < 0 then Right will win, regardless of who plays first.
- If x = 0 then the player who goes second will win.
- If x || 0 then the player who goes first will win.
More generally, we can define G > H as G - H > 0, and similarly for <, = and ||.
The notation G || H means that G and H are incomparable. G || H is equivalent to G−H || 0, i.e that G > H, G < H and G = H are all false. Incomparable games are sometimes said to be confused with each other, because one or the other may be preferred by a player depending on what is added to it. A game confused with zero is said to be fuzzy, as opposed to positive, negative, or zero. An example of a fuzzy game is star (*).
Sometimes when a game nears the end, it will decompose into several smaller games that do not interact, except in that each player's turn allows moving in only one of them. For example, in Go, the board will slowly fill up with pieces until there are just a few small islands of empty space where a player can move. Each island is like a separate game of Go, played on a very small board. It would be useful if each subgame could be analyzed separately, and then the results combined to give an analysis of the entire game. This doesn't appear to be easy to do. For example, you might have two subgames where whoever moves first wins, but when they are combined into one big game, it's no longer the first player who wins. Fortunately, there is a way to do this analysis. Just use the following remarkable theorem:
- If a big game decomposes into two smaller games, and the small games have associated Games of x and y, then the big game will have an associated Game of x+y.
A game composed of smaller games is called the disjunctive sum of those smaller games, and the theorem states that the method of addition we defined is equivalent to taking the disjunctive sum of the addends.
Historically, Conway developed the theory of surreal numbers in the reverse order of how it has been presented here. He was analyzing Go endgames, and realized that it would be useful to have some way to combine the analyses of non-interacting subgames into an analysis of their disjunctive sum. From this he invented the concept of a Game and the addition operator for it. From there he moved on to developing a definition of negation and comparison. Then he noticed that a certain class of Games had interesting properties; this class became the surreal numbers. Finally, he developed the multiplication operator, and proved that the surreals are actually a field, and that it includes both the reals and ordinals.
[edit] Alternative realization
Since Conway first introduced surreal numbers, several alternative constructions have been developed.
[edit] Sign expansion
[edit] Definitions
In one alternative realization, called the sign-expansion or sign-sequence of a surreal number, a surreal number is a function whose domain is an ordinal and whose range is { − 1, + 1 }.
Define the binary predicate "simpler than" on numbers by x is simpler than y if x is a proper subset of y, i.e. if dom(x) < dom(y) and x(α) = y(α) for all α < dom(x).
For surreal numbers define the binary relation < to be lexicographic order (with the convention that "undefined values" are greater than −1 and less than 1). So x < y if one of the following holds:
- x is simpler than y and y(dom(x)) = + 1;
- y is simpler than x and x(dom(y)) = − 1;
- there exists a number z such that z is simpler than x, z is simpler than y, x(dom(z)) = − 1 and y(dom(z)) = + 1.
Equivalently, let δ(x,y) = min({ dom(x), dom(y)} ∪ { α : α < dom(x) ∧ α < dom(y) ∧ x(α) ≠ y(α) }), so that x = y if and only if δ(x,y) = dom(x) = dom(y). Then, for numbers x and y, x < y if and only if one of the following holds:
- δ(x,y) = dom(x) ∧ δ(x,y) < dom(y) ∧ y(δ(x,y)) = + 1;
- δ(x,y) < dom(x) ∧ δ(x,y) = dom(y) ∧ x(δ(x,y)) = − 1;
- δ(x,y) < dom(x) ∧ δ(x,y) < dom(y) ∧ x(δ(x,y)) = − 1 ∧ y(δ(x,y)) = + 1.
For numbers x and y, x ≤ y if and only if x < y ∨ x = y, x > y if and only if y < x, and x ≥ y if and only if y ≤ x.
< is transitive, and for all numbers x and y, exactly one of x < y, x = y, x > y, holds (law of trichotomy). This means that < is a linear order (except that < is a proper class).
For sets of numbers, L and R such that ∀x ∈ L ∀y ∈ R (x < y), there exists a unique number z such that
- ∀x ∈ L (x < z) ∧ ∀y ∈ R (z < y),
- For any number w such that ∀x ∈ L (x < w) ∧ ∀y ∈ R (w < y), w = z or z is simpler than w.
Furthermore, z is constructible from L and R by transfinite induction. z is the simplest number between L and R. Let the unique number z be denoted by σ(L,R).
For a number x, define its left set L(x) and right set R(x) by
- L(x) = { x|α : α < dom(x) ∧ x(α) = + 1 };
- R(x) = { x|α : α < dom(x) ∧ x(α) = − 1 },
then σ(L(x),R(x)) = x.
One advantage of this alternative realization is that equality is identity, not an inductively defined relation. Unlike Conway's realization of the surreal numbers, however, the sign-expansion requires a prior construction of the ordinals, while in Conway's realization, the ordinals are constructed as particular cases of surreals.
However, similar definitions can be made that obviate the need for prior construction of the ordinals. For instance, we could let the surreals be the (recursively-defined) class of functions whose domain is a subset of the surreals satisfying the transitivity rule
- ∀g ∈ dom f (∀h ∈ dom g (h ∈ dom f ))
and whose range is { −, + }. "Simpler than" is very simply defined now—x is simpler than y if x ∈ dom y. The total ordering is defined by considering x and y as sets of ordered pairs (as a function is normally defined): Either x = y, or else the surreal number z = x ∩ y is in the domain of x or the domain of y (or both, but in this case the signs must disagree). We then have x < y if x(z) = − or y(z) = + (or both). Converting these functions into sign sequences is a straightforward task; arrange the elements of dom f in order of simplicity (i.e., inclusion), and then write down the signs that f assigns to each of these elements in order. The ordinals then occur naturally as those surreal numbers whose range is { + }.
[edit] Addition and multiplication
The sum x + y of two numbers, x and y, is defined by induction on dom(x) and dom(y) by x + y = σ(L,R), where
- L = { u + y : u ∈ L(x) } ∪{ x + v : v ∈ L(y) },
- R = { u + y : u ∈ R(x) } ∪{ x + v : v ∈ R(y) }.
The additive identity is given by the number 0 = { }, i.e. the number 0 is the unique function whose domain is the ordinal 0, and the additive inverse of the number x is the number − x, given by dom(− x) = dom(x), and, for α < dom(x), (− x)(α) = − 1 if x(α) = + 1, and (− x)(α) = + 1 if x(α) = − 1.
It follows that a number x is positive if and only if 0 < dom(x) and x(0) = + 1, and x is negative if and only if 0 < dom(x) and x(0) = − 1.
The product xy of two numbers, x and y, is defined by induction on dom(x) and dom(y) by xy = σ(L,R), where
- L = { uy + xv − uv : u ∈ L(x), v ∈ L(y) } ∪ { uy + xv − uv : u ∈ R(x), v ∈ R(y) },
- R = { uy + xv − uv : u ∈ L(x), v ∈ R(y) } ∪ { uy + xv − uv : u ∈ R(x), v ∈ L(y) }.
The multiplicative identity is given by the number 1 = { (0,+ 1) }, i.e. the number 1 has domain equal to the ordinal 0, and 1(0) = + 1.
[edit] Correspondence with Conway
The map from Conway's realization to sign expansions is given by f({ L | R }) = σ(M,S), where M = { f(x) : x ∈ L } and S = { f(x) : x ∈ R }.
The inverse map from the alternative realization to Conway's realization is given by g(x) = { L | R }, where L = { g(y) : y ∈ L(x) } and R = { g(y) : y ∈ R(x) }.
[edit] Axiomatic approach
In another approach to the surreals, given in Alling[3] explicit construction is bypassed altogether. Instead, a set of axioms is given that any particular approach to the surreals must satisfy. Much like the axiomatic approach to the reals, these axioms guarantee uniqueness up to isomorphism.
A triple  is a surreal number system iff:
is a surreal number system iff:
- < is a total order over No
- b is a function from No onto the class of all ordinals (b is called the "birthday function" on No).
- Let A and B be subclasses of No such that for all x ∈ A and y ∈ B, x < y (using Alling's terminology, 〈 A,B 〉 is a "Conway cut" of No). Then there exists a unique z ∈ No such that b(z) is minimal and for all x ∈ A and all y ∈ B, x < z < y. (This axiom is often referred to as "Conway's Simplicity Theorem".)
- Furthermore, if an ordinal α is greater than b(x) for all x ∈ A, B, then b(z) ≤ α. (Alling calls a system that satisfies this axiom a "full surreal number system".)
It should be noted that both Conway's original construction and the sign-expansion construction of surreals satisfy these axioms.
Given these axioms, Alling[3] derives Conway's original definition of ≤ and develops surreal arithmetic.
[edit] See also
[edit] Notes
- ^ In the original formulation using von Neumann–Bernays–Gödel set theory, the surreals form a proper class, rather than a set, so the term field is not precisely correct; where this distinction is important, some authors use Field or FIELD to refer to a proper class that has the arithmetic properties of a field. One can obtain a true field by limiting the construction to a Grothendieck universe, yielding a set with the cardinality of some strongly inaccessible cardinal, or by using a form of set theory in which constructions by transfinite recursion stop at some countable ordinal such as epsilon nought.
- ^ O'Connor, J.J.; Robertson, E.F., Conway Biography, http://www-history.mcs.st-andrews.ac.uk/Biographies/Conway.html, retrieved on 2008-01-24
- ^ a b Foundations of Analysis over Surreal Number Fields. Alling, Norman L. North-Holland 1987
[edit] Further reading
- Donald Knuth's original exposition: Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. 1974, ISBN 0-201-03812-9. More information can be found at the book's official homepage
- An update of the classic 1976 book defining the surreal numbers, and exploring their connections to games: On Numbers And Games, 2nd ed., John Conway, 2001, ISBN 1-56881-127-6.
- An update of the first part of the 1981 book that presented surreal numbers and the analysis of games to a broader audience: Winning Ways for Your Mathematical Plays, vol. 1, 2nd ed., Berlekamp, Conway, and Guy, 2001, ISBN 1-56881-130-6.
- Martin Gardner, Penrose Tiles to Trapdoor Ciphers, W. H. Freeman & Co., 1989. ISBN 0-7167-1987-8. Chapter 4 — not especially technical overview; reprints the 1976 Scientific American article.
- Polly Shulman, "Infinity Plus One, and Other Surreal Numbers". Discover, December 1995. Discussed online at the "Ask Dr. Math" forum.
- A detailed, though somewhat technical, treatment of surreal numbers: Foundations of Analysis over Surreal Number Fields, Alling, Norman L., 1987, ISBN 0-444-70226-1
- A treatment of surreals based on the sign-expansion realization: An Introduction to the Theory of Surreal Numbers, Goshnor, Harry, 1986, ISBN 0-521-31205-1
- A detailed philosophical development of the concept of surreal numbers as a most general concept of number is Alain Badiou, Number and Numbers (New York: Polity Press, 2008): ISBN 0745638791 (paperback); ISBN 0745638783 (hardcover)
[edit] External links
- Hackenstrings, and the 0.999... ?= 1 FAQ, by A. N. Walker
- A gentle yet thorough introduction by Claus Tøndering
- Surreal number on PlanetMath
- Good Math, Bad Math: Surreal Numbers, a series of articles about surreal numbers, their variations, and their applications
|
|||||||||||


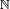 )
) )
) )
)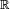 )
) )
)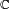 )
) )
) )
)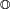 )
) )
)
