Purely functional
From Wikipedia, the free encyclopedia
| This article is written like a personal reflection or essay and may require cleanup. Please help improve it by rewriting it in an encyclopedic style. (December 2007) |
Purely functional is a term in computing used to describe algorithms, data structures or programming languages that exclude destructive modifications (updates). According to this restriction, variables are used in a mathematical sense, with identifiers referring to immutable, persistent values.
Contents |
[edit] Benefits and applications
The persistence property of purely functional data structures can be advantageous in the development of many applications which deal with multiple versions of an object.
For example, consider a comprehensive web-based thesaurus service that uses a large red-black tree to store its list of synonym relationships, and that allows each user to add their own custom words to their personal thesaurus. One way to do this is to make a copy of the tree for each user, and then add their custom words to it; however, this is wasteful duplication. Moreover, it would cause a significant processing delay to make the complete copy of the tree.
A better approach is to store the words in an immutable (and therefore purely functional) red-black tree. Then, one can simply take the original version and produce a new tree based on it for each set of custom words. Because these new trees share large amounts of structure with the main tree, the space overhead for each additional user is at most 2klog2n, where k is the number of custom nodes. With a mutable red-black tree, this approach would not work, since changes to the main tree would affect all users.
Besides their efficiency benefits, the inherent referential transparency of functional data structures tends to make purely functional computation more amenable to analysis and optimization, both formal and informal.
[edit] Examples of purely functional data structures
| It has been suggested that this article or section be merged into Persistent data structure. (Discuss) |
[edit] Linked lists
This example is taken from Okasaki. See the bibliography.
Singly linked lists are a bread and butter data structure in functional languages. In ML-derived languages and Haskell, they are purely functional because once a node in the list has been allocated, it cannot be modified, only copied or destroyed.
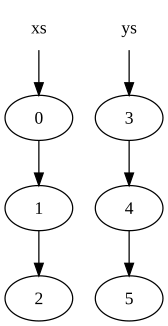
Consider the two lists:
xs = [0, 1, 2] ys = [3, 4, 5]
These would be represented in memory by:
where a circle indicates a node in the list (the arrow out showing the second element of the node which is a pointer to another node).
Now concatenating the two lists:
zs = xs ++ ys
results in the following memory structure:
Notice that the nodes in list xs have been copied, but the nodes in ys are shared. As a result, the original lists (xs and ys) persist and have not been modified.
The reason for the copy is that the last node in xs (the node containing the original value 2) cannot be modified to point to the start of ys, because that would change the value of xs.
[edit] Trees
This example is taken from Okasaki. See the bibliography.
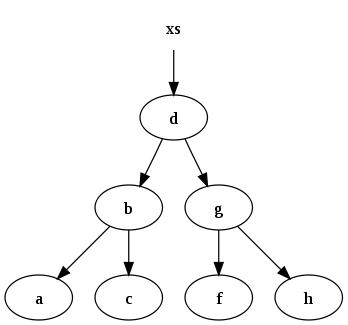
Consider a binary tree used for fast searching, where every node has the recursive invariant that subnodes on the left are less than the node, and subnodes on the right are greater than the node.
For instance, the set of data
xs = [a, b, c, d, f, g, h]
might be represented by the following binary search tree:
A function which inserts data into the binary tree and maintains the invariant is:
fun insert (x, E) = T (E, x, E)
| insert (x, s as T (a, y, b)) =
if x < y then T (insert (x, a), y, b)
else if x > y then T (a, y, insert (x, b))
else s
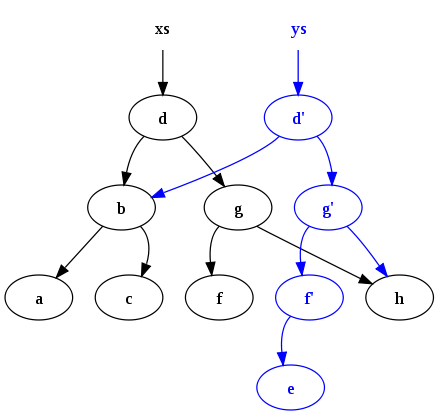
After executing
ys = insert ("e", xs)
we end up with the following:
Notice two points: Firstly the original tree (xs) persists. Secondly many common nodes are shared between the old tree and the new tree. Such persistence and sharing is difficult to manage without some form of garbage collection (GC) to automatically free up nodes which have no live references, and this is why GC is a feature commonly found in functional programming languages.
[edit] Reference cycles
Since every value in a purely functional computation is built up out of existing values, it would seem that it is impossible to create a cycle of references. In that case, the reference graph (the graph of the references from object to object) could only be a directed acyclic graph. However, in most functional languages, functions can be defined recursively; this capability allows recursive structures using functional suspensions. In lazy languages, such as Haskell, all data structures are represented as implicitly suspended thunks; in these languages any data structure can be recursive. Some other languages, such as Objective Caml, allow the explicit definition of recursive values.
[edit] See also
[edit] External links
- Purely Functional Data Structures thesis by Chris Okasaki (PDF format)
- Making Data-Structures Persistent by James R. Driscoll, Neil Sarnak, Daniel D. Sleator, Robert E. Tarjan (PDF)
- Fully Persistent Lists with Catenation by James R. Driscoll, Daniel D. Sleator, Robert E. Tarjan (PDF)
- Persistent Data Structures from MIT open course Advanced Algorithms
[edit] Bibliography
Purely functional data structures by Chris Okasaki, Cambridge University Press, 1998, ISBN 0-521-66350-4.