Trigonometry
From Wikipedia, the free encyclopedia
| This article needs additional citations for verification. Please help improve this article by adding reliable references (ideally, using inline citations). Unsourced material may be challenged and removed. (February 2009) |
| This article includes a list of references or external links, but its sources remain unclear because it lacks inline citations. Please improve this article by introducing more precise citations where appropriate. (February 2009) |


Trigonometry (from Greek trigōnon "triangle" + metron "measure")[1] is a branch of mathematics that deals with triangles, particularly those plane triangles in which one angle has 90 degrees (right triangles). Trigonometry deals with relationships between the sides and the angles of triangles and with the trigonometric functions, which describe those relationships.
Trigonometry has applications in both pure mathematics and in applied mathematics, where it is essential in many branches of science and technology. It is usually taught in secondary schools either as a separate course or as part of a precalculus course. Trigonometry is informally called "trig".
A branch of trigonometry, called spherical trigonometry, studies triangles on spheres, and is important in astronomy and navigation.
Contents |
[edit] History
Development of Trigonometry is not the work of any one man or nation. Its history spans thousands of years and has touched every major civilization. It first originated in India and the basic concepts of angle and measurements was noted in Vedic texts such as Srimad Bhagavatam [2]. However, Trigonometry in its present form was established in Surya-siddhanta and later by Aryabhata [5th century CE]. It should be noted that from the time of Hipparchus until modern times there was no such thing as a trigonometric ratio. Instead, the Indian civilization and after them the Greeks and the Muslims used trigonometric lines. These lines first took the form of chords and later half chords, or sines. These chord and sine lines would then be associated with numerical values, possibly approximations, and listed in trigonometric tables
[edit] Overview
If one angle of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are complementary angles. The shape of a right triangle is completely determined, up to similarity, by the angles. This means that once one of the other angles is known, the ratios of the various sides are always the same regardless of the overall size of the triangle. These ratios are given by the following trigonometric functions of the known angle A, where a, b and c refer to the lengths of the sides in the accompanying figure:
- The sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.
- The cosine function (cos), defined as the ratio of the adjacent leg to the hypotenuse.
- The tangent function (tan), defined as the ratio of the opposite leg to the adjacent leg.
The hypotenuse is the side opposite to the 90 degree angle in a right triangle; it is the longest side of the triangle, and one of the two sides adjacent to angle A. The adjacent leg is the other side that is adjacent to angle A. The opposite side is the side that is opposite to angle A. The terms perpendicular and base are sometimes used for the opposite and adjacent sides respectively. Many people find it easy to remember what sides of the right triangle are equal to sine, cosine, or tangent, by memorizing the word SOH-CAH-TOA (see below under Mnemonics).
The reciprocals of these functions are named the cosecant (csc or cosec), secant (sec) and cotangent (cot), respectively. The inverse functions are called the arcsine, arccosine, and arctangent, respectively. There are arithmetic relations between these functions, which are known as trigonometric identities.
With these functions one can answer virtually all questions about arbitrary triangles by using the law of sines and the law of cosines. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and an angle or two angles and a side or three sides are known. These laws are useful in all branches of geometry, since every polygon may be described as a finite combination of triangles.
[edit] Extending the definitions
The above definitions apply to angles between 0 and 90 degrees (0 and π/2 radians) only. Using the unit circle, one can extend them to all positive and negative arguments (see trigonometric function). The trigonometric functions are periodic, with a period of 360 degrees or 2π radians. That means their values repeat at those intervals.
The trigonometric functions can be defined in other ways besides the geometrical definitions above, using tools from calculus and infinite series. With these definitions the trigonometric functions can be defined for complex numbers. The complex function cis is particularly useful
See Euler's and De Moivre's formulas.
[edit] Mnemonics
Students often use mnemonics to remember facts and relationships in trigonometry. For example, the sine, cosine, and tangent ratios in a right triangle can be remembered by representing them as strings of letters, as in SOH-CAH-TOA.
- Sine = Opposite ÷ Hypotenuse
- Cosine = Adjacent ÷ Hypotenuse
- Tangent = Opposite ÷ Adjacent
Alternatively, one can devise sentences which consist of words beginning with the letters to be remembered. Some examples of mnemonics are "Silly Old Hitler Couldn't Advance His Troops Over Africa" and "Some Officers Have Curly Auburn Hair Till Old Age"[3]. However, any memorable phrase constructed of words beginning with the letters S-O-H-C-A-H-T-O-A will serve. Some other examples include Some Old Hags Can't Always Hide Their Old Age and Sir Oliver's Horse Came Ambling Home To Oliver's Aunt.
It is of ethnographic interest to note that the mnemonic TOA-CAH-SOH can be translated in the local Singaporean Hokkien dialect to 'big-legged woman', serving as an additional learning aid for students in Singapore.[4][unreliable source?]
Another type of mnemonic describes facts in a simple, memorable way, such as "Plus to the right, minus to the left; positive height, negative depth," which refers to trigonometric functions generated by a revolving line.
[edit] Calculating trigonometric functions
Trigonometric functions were among the earliest uses for mathematical tables. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate between the values listed to get higher accuracy. Slide rules had special scales for trigonometric functions.
Today scientific calculators have buttons for calculating the main trigonometric functions (sin, cos, tan and sometimes cis) and their inverses. Most allow a choice of angle measurement methods: degrees, radians and, sometimes, Grad. Most computer programming languages provide function libraries that include the trigonometric functions. The floating point unit hardware incorporated into the microprocessor chips used in most personal computers have built-in instructions for calculating trigonometric functions.
[edit] Applications of trigonometry
There are an enormous number of applications of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.
Fields which make use of trigonometry or trigonometric functions include astronomy (especially, for locating the apparent positions of celestial objects, in which spherical trigonometry is essential) and hence navigation (on the oceans, in aircraft, and in space), music theory, acoustics, optics, analysis of financial markets, electronics, probability theory, statistics, biology, medical imaging (CAT scans and ultrasound), pharmacy, chemistry, number theory (and hence cryptology), seismology, meteorology, oceanography, many physical sciences, land surveying and geodesy, architecture, phonetics, economics, electrical engineering, mechanical engineering, civil engineering, computer graphics, cartography, crystallography and game development.

[edit] Common formulae
Certain equations involving trigonometric functions are true for all angles and are known as trigonometric identities. Many express important geometric relationships. For example, the Pythagorean identities are an expression of the Pythagorean Theorem. Here are some of the more commonly used identities, as well as the most important formulae connecting angles and sides of an arbitrary triangle. For more identities see trigonometric identity.
Sho Minamimoto, a character from the video game "The World Ends With You", often uses the acronym "SOHCAHTOA."
[edit] Triangle identities
In the following identities, A, B and C are the angles of a triangle and a, b and c are the lengths of sides of the triangle opposite the respective angles.
[edit] Law of sines
The law of sines (also know as the "sine rule") for an arbitrary triangle states:
where R is the radius of the circumcircle of the triangle:
[edit] Law of cosines
The law of cosines ( known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:
or equivalently:
[edit] Law of tangents
The law of tangents:
[edit] See also
- Uses of trigonometry
- Trigonometric functions
- List of basic trigonometry topics
- List of trigonometric identities
- Trigonometry in Galois fields
- List of triangle topics
- Rational trigonometry
- Unit circle
[edit] Notes
- ^ "trigonometry". Online Etymology Dictionary. http://www.etymonline.com/index.php?search=trigonometry.
- ^ "Vedic Cosmography and Astronomy By Richard L. Thompson". 194. http://books.google.com/books?isbn=8120819543.
- ^ "What does SOHCAHTOA stand for?". Acronym Finder. http://www.acronymfinder.com/Some-Officers-Have-Curly-Auburn-Hair-Till-Old-Age-(mnemonic-for-remembering-sine,-cosine-and-tangent)-(SOHCAHTOA).html. Retrieved on 2008-10-27.
- ^ "Trigonometry - My Grandmother Also Can Do This!". http://www.exampaper.com.sg/questions/e-maths/trigonometry-my-grandmother-also-can-do-this. Retrieved on 2008-08-30. Diary of a Private O Level Maths Tutor in Singapore
[edit] References
- Christopher M. Linton (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy . Cambridge University Press.
- Weisstein, Eric W. "Trigonometric Addition Formulas". Wolfram MathWorld.
[edit] External links
![]() Textbooks from Wikibooks
Textbooks from Wikibooks
![]() Quotations from Wikiquote
Quotations from Wikiquote
![]() Source texts from Wikisource
Source texts from Wikisource
![]() Images and media from Commons
Images and media from Commons
![]() News stories from Wikinews
News stories from Wikinews
- Trigonometric Delights, by Eli Maor, Princeton University Press, 1998. Ebook version, in PDF format, full text presented.
- Trigonometry by Alfred Monroe Kenyon and Louis Ingold, The Macmillan Company, 1914. In images, full text presented.
- Trigonometry on Mathwords.com index of trigonometry entries on Mathwords.com
- Benjamin Banneker's Trigonometry Puzzle at Convergence
- Dave's Short Course in Trigonometry by David Joyce of Clark University
|
|||||










![\begin{align}
\frac{a}{\sin A} & = \frac{b}{\sin B}=\frac{c}{\sin C} \\[5pt]
\cos C & = \frac{a^2+b^2-c^2}{2ab}
\end{align}](http://upload.wikimedia.org/math/f/1/1/f11a7cfaf1594115552a81b0e0acff19.png)
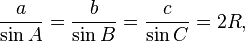
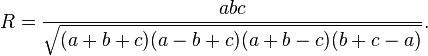
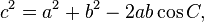

![\frac{a+b}{a-b}=\frac{\tan\left[\tfrac{1}{2}(A+B)\right]}{\tan\left[\tfrac{1}{2}(A-B)\right]}](http://upload.wikimedia.org/math/8/e/c/8ecc3d7514a107662d79d2b6e0678995.png)

