Hash table

From Wikipedia, the free encyclopedia

A small phone book as a hash table.

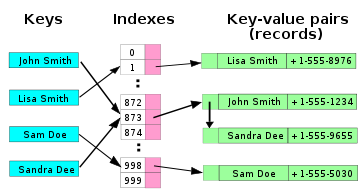
In computer science, a hash table or hash map is a data structure that uses a hash function to efficiently translate certain keys (e.g., person names) into associated values (e.g., their telephone numbers). The hash function is used to transform the key into the index (the hash) of an array element (the slot or bucket) where the corresponding value is to be sought.

Ideally the hash function should map each possible key to a different slot index; but this goal is rarely achievable in practice. Most hash table designs assume that hash collisions — pairs of different keys with the same hash values — are normal occurrences, and accomodate them in some way.

In a well-dimensioned hash table, the average cost (number of instructions) for each lookup is independent of the number of elements stored in the table. Many hash table designs also allow arbitrary insertions and deletions of key-value pairs, at constant average (indeed, amortized) cost per operation.^[1][2]

In many situations, hash tables turn out to be more efficient than search trees or any other table lookup structure. For this reason, they are widely used in all kinds of computer software.

[edit] Uses

[edit] Associative tables

Hash tables are commonly used to implement all sort of in-memory tables. They are used to implement associative arrays (arrays whose indices are arbitrary strings or other complicated objects), especially in interpreted programming languages like gawk and perl.

[edit] Database indices

Hash tables may also be used for disk-based persistent data structures and database indices, although balanced trees are more popular in these applications.

[edit] Sets

Besides recovering the entry which has a given key, many hash table implementations can also tell whether such an entry exists or not.

Those structures can therefore be used to implement a set data structure, which merely records whether a given key belongs to a specified set of keys. In this case, the structure can be simplified by eliminating all parts which have to do with the entry values. Hashing can be used to implement both static and dynamic sets.

[edit] Features

The main advantage of hash tables over other table data structures is speed. This advantage is more apparent when the number of entries is large (thousands or more). Hash tables are particularly efficient when the maximum number of entries can be predicted in advance, so that the bucket array can be allocated once with the optimum size and never resized.

If the set of key-value pairs is fixed and known ahead of time (so insertions and deletions are not allowed), one may reduce the average lookup cost by a careful choice of the hash function, bucket table size, and internal data structures. In particular, one may be able to devise a hash function that is collision-free, or even perfect (see below). In this case the keys need not be stored in the table.

[edit] Drawbacks

Hash tables are more difficult to implement than efficient search trees, such as Sleator and Tarjan's self-balancing binary search trees. Choosing an effective hash function for a specific application is more an art than a science. In open-addressed hash tables it is fairly easy to create a poor hash function.

Although hash table lookups use constant time on average, the cost of a good hash function can be significantly higher than the inner loop of the lookup algorithm for typical search tree. Thus hash tables are not efficient for small tables.

For certain string processing applications, such as spell-checking, hash tables are less efficient than tries or finite automata. Also, If each key is represented by a small enough number of bits, then, instead of a hash table, one may use the key directly as the index into an array of values. Note that there are no collisions in this case.

The entries stored in a hash table can be enumerated efficiently (at constant cost per entry), but only in some pseudo-random order. Listing all n entries in some specific order generally requires a separate sorting step, whose cost per entry proportional to log(n). In comparison, ordered search trees have insertion cost proportional to log(n) but allow listing of all entries, in the search order, at constant cost per entry.

If the the keys are not stored (because the hash function is collision-free), there may be no easy way to enumerate the keys that are present in the table at any given moment.

Although the average cost per operation is constant and fairly small, the cost of a single operation may be quite high. In particular, if the the hash table uses dynamic resizing, an insertion or deletion operation may occasionally take time proportional to the number of entries. This may be a serious drawback in real-time or interactive applications.

Hash tables in general exhibit poor locality of reference—that is, the data to be accessed is distributed seemingly at random in memory. Because hash tables cause access patterns that jump around, this can trigger microprocessor cache misses that cause long delays. Compact data structures such as arrays, searched with linear search, may be faster if the table is relatively small and keys are integers or other short strings. According to Moore's Law, cache sizes are growing exponentially and so what is considered "small" may be increasing. The optimal performance point varies from system to system.

Hash tables become quite inefficient when there are many collisions. While extremely uneven hash distributions are extremely unlikely to arise by chance, a malicious adversary with knowledge of the hash function may be able to supply information to a hash which creates worst-case behavior by causing excessive collisions, resulting in very poor performance (i.e., a denial of service attack). In critical applications, either universal hashing can be used or a data structure with better worst-case guarantees may be preferable.^[3]

[edit] Collision resolution

Collisions are practically unavoidable when hashing a random subset of a large set of possible keys. For example, if 2500 keys are hashed into a million buckets, even with a perfectly uniform random distribution, there is a 95% chance of two or more keys being hashed to the same slot.

Therefore, most hash table implementations have some collision resolution strategy to handle such events. Some common strategies are described below.

[edit] Separate chaining

Hash collision resolved by chaining.

Sometimes called simply chaining or direct chaining, in its simplest form each slot in the array is a linked list, or the head cell of a linked list, where the list contains the elements that hashed to the same location. Insertion requires finding the correct slot, then appending to either end of the list in that slot; deletion requires searching the list and removal.

Chained hash tables have advantages over open addressed hash tables in that the removal operation is simple and resizing the table can be postponed for a much longer time because performance degrades more gracefully even when every slot is used. Indeed, many chaining hash tables may not require resizing at all since performance degradation is linear as the table fills. For example, a chaining hash table containing twice its recommended capacity of data would only be about twice as slow on average as the same table at its recommended capacity.

Chained hash tables inherit the disadvantages of linked lists. When storing small records, the overhead of the linked list can be significant. An additional disadvantage is that traversing a linked list has poor cache performance.

Alternative data structures can be used for chains instead of linked lists. By using a self-balancing tree, for example, the theoretical worst-case time of a hash table can be brought down to O(log n) rather than O(n). However, since each list is intended to be short, this approach is usually inefficient unless the hash table is designed to run at full capacity or there are unusually high collision rates, as might occur in input designed to cause collisions. Dynamic arrays can also be used to decrease space overhead and improve cache performance, forming a cache-conscious resolution scheme as discussed in the section Cache-conscious collision resolution.

Some chaining implementations use an optimization where the first record of each chain is stored in the table. ^[2] The purpose is to increase cache efficiency of hash table access. In order to avoid wasting large amounts of space, such hash tables would maintain a load factor of 1.0 or greater. The term direct chaining is sometimes used to describe implementations that do not use this optimization.

[edit] Open addressing

Hash collision resolved by linear probing (interval=1).

Open addressing hash tables store the records directly within the array. This approach is also called closed hashing. A hash collision is resolved by probing, or searching through alternate locations in the array (following a probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. ^[4] Well known probe sequences include:

linear probing 

in which the interval between probes is fixed - often at 1.

quadratic probing 

in which the interval between probes increases proportional to the square of the probe number (the interval thus increasing linearly and the indices are described by a quadratic function).

double hashing 

in which the interval between probes is computed by another hash function.

[edit] Open addressing versus chaining

Chained hash tables have the following benefits over open addressing:

• They are simple to implement effectively and only require basic data structures.
• From the point of view of writing suitable hash functions, chained hash tables are insensitive to clustering, only requiring minimization of collisions. Open addressing depends upon better hash functions to avoid clustering. This is particularly important if novice programmers can add their own hash functions, but even experienced programmers can be caught out by unexpected clustering effects.
• They degrade in performance more gracefully. Although chains grow longer as the table fills, a chained hash table cannot "fill up" and does not exhibit the sudden increases in lookup times that occur in a near-full table with open addressing. (see chart)
• If the hash table stores large records, about 5 or more words per record, chaining uses less memory than open addressing.
• If the hash table is sparse (that is, it has a big array with many free array slots), chaining uses less memory than open addressing even for small records of 2 to 4 words per record due to its external storage.

This graph compares the average number of cache misses required to lookup elements in tables with chaining and linear probing. As the table passes the 80%-full mark, linear probing's performance drastically degrades.

For small record sizes (a few words or less) the benefits of in-place open addressing compared to chaining are:

• They can be more space-efficient than chaining since they don't need to store any pointers or allocate any additional space outside the hash table. Simple linked lists require a word of overhead per element.
• Insertions avoid the time overhead of memory allocation, and can even be implemented in the absence of a memory allocator.
• Because it uses internal storage, open addressing avoids the extra indirection required for chaining's external storage. It also has better locality of reference, particularly with linear probing. With small record sizes, these factors can yield better performance than chaining, particularly for lookups.
• They can be easier to serialize, because they don't use pointers.

On the other hand, normal open addressing is a poor choice for large elements, since these elements fill entire cache lines (negating the cache advantage), and a large amount of space is wasted on large empty table slots. If the open addressing table only stores references to elements (external storage), it uses space comparable to chaining even for large records but loses its speed advantage.

Generally speaking, open addressing is better used for hash tables with small records that can be stored within the table (internal storage) and fit in a cache line. They are particularly suitable for elements of one word or less. In cases where the tables are expected to have high load factors, the records are large, or the data is variable-sized, chained hash tables often perform as well or better.

Ultimately, used sensibly, any kind of hash table algorithm is usually fast enough; and the percentage of a calculation spent in hash table code is low. Memory usage is rarely considered excessive. Therefore, in most cases the differences between these algorithms is marginal, and other considerations typically come into play.

[edit] Coalesced hashing

A hybrid of chaining and open addressing, coalesced hashing links together chains of nodes within the table itself. ^[4] Like open addressing, it achieves space usage and (somewhat diminished) cache advantages over chaining. Like chaining, it does not exhibit clustering effects; in fact, the table can be efficiently filled to a high density. Unlike chaining, it cannot have more elements than table slots.

[edit] Perfect hashing

If all of the keys that will be used are known ahead of time, and there are no more keys than can fit the hash table, perfect hashing can be used to create a perfect hash table, in which there will be no collisions. If minimal perfect hashing is used, every location in the hash table can be used as well.

Perfect hashing allows for constant time lookups in the worst case. This is in contrast to chaining and open addressing methods, where the time for lookup is low on average, but may be arbitrarily large. A simpler alternative, which also gives worst case constant lookup time, is cuckoo hashing.

[edit] Dynamic perfect hashing

In dynamic perfect hashing,^[5] a guarantee of constant worst-case lookup times by using a second-level hash table with no collisions for each bucket is given. If there are k elements in the bucket, the bucket's hash table is given size k², and its hash function is selected at random from a universal hash function set. If a collision ever occurs, the table is rebuilt with a different randomly-selected hash function. Because the load factor of the table is kept low (1/k), rebuilding is infrequent and amortized cost of insertions is low.

Although each bucket requires quadratic space, if the keys inserted into the (first-level) hash table are uniformly distributed, the structure as a whole occupies expected O(n) space, since bucket sizes are small with high probability.

[edit] Probabilistic hashing

Perhaps the simplest solution to a collision is to replace the value that is already in the slot with the new value, or slightly less commonly, drop the record that is to be inserted. In later searches, this may result in a search not finding a record which has been inserted. This technique is particularly useful for implementing caching.

An even more space-efficient solution which is similar to this is use a bit array (an array of one-bit fields) for our table. Initially all bits are set to zero, and when we insert a key, we set the corresponding bit to one. False negatives cannot occur, but false positives can, since if the search finds a 1 bit, it will claim that the value was found, even if it was just another value that hashed into the same array slot by coincidence. In reality, such a hash table is merely a specific type of Bloom filter.

[edit] Robin Hood hashing

One interesting variation on double-hashing collision resolution is that of Robin Hood hashing^[6]. The idea is that a key already inserted may be displaced by a new key if its probe count is larger than the key at the current position. The net effect of this is that it reduces worst case search times in the table. This is similar to Knuth's ordered hash tables except the criteria for bumping a key does not depend on a direct relationship between the keys. Since both the worst case and the variance on the number of probes is reduced dramatically an interesting variation is to probe the table starting at the expected successful probe value and then expand from that position in both directions.^[7]

[edit] Cache-conscious collision resolution

A chained hash table is a simple and flexible data structure but it does not make good use of CPU cache. This is especially the case when variable-length strings are used as keys. When a collision occurs, a linked list is traversed which can attract a surplus of cache-misses. In addition, linked lists will waste an excessive amount of space due to pointers and memory allocation overheads. We can address these issues by replacing linked lists with dynamic arrays, forming a cache-conscious hash table known as an array hash.^[8]

When a string is hashed to a slot, it is appended to the end of the dynamic array that is assigned to that slot. In this manner, nodes and pointers are eliminated and strings are accessed in a sequential manner, promoting good use of cache. The array hash was also shown to be substantially faster and more compact than a chained hash table using 32-bit or 64-bit integer keys. ^[9]

[edit] Performance analysis

[edit] Load factor

The load factor of a hash table is the ratio n/s between the number n of key-value pairs stored in the table and the size s of the bucket array. With a good hash function, the average lookup cost grows relatively slowly as the load factor increases, up to 0.7 or so. For larger load factors both the probability of collisions and the cost of handling them increase quite rapidly. In the limit, when the load factor is n (i.e. when s is 1), the hashing provides no benefit.

On the other hand, as the load factor approaches zero, the size of the hash table increases with little improvement in the search cost.

[edit] Operation cost

The cost of a hash table lookup is that of computing the hash function and then scanning the entries of the selected bucket for the desired key. The worst-case scenario is when all entries were inserted into the same bucket, in which case the hash table is ineffective and the cost is that of searching the bucket structure. If that list is linear and unsorted, then all entries have to be scanned, so the cost is proportional to the number n of entries in the table.

On the other hand, if the ditribution of keys is sufficiently uniform, the average cost of a lookup depends only on the load factor, not on the number of entries the table sizea. These corner cases are addressed in mathematical analysis with the Simple Uniform Hashing Assumption, which puts basic assumed conditions on the hash function.

[edit] Dynamic resizing

In order to keep the load factor in a definite range, e.g. between 1/4 and 3/4, many table implementations may expand the table dynamically when items are inserted, and may shrink it when items are deleted. In Java's HashMap class, for example, the default load factor threshold for table expansion is 0.75.

Specifically, when the load factor exceeds some threshold r_max, a new larger table is allocated, all the entries of the old table are removed and inserted into this new table, and the old table is returned to the free storage pool. Symmetrically, when the load factor falls below a second threshold r_min, all entries are moved to a new smaller table. If the table size increases or decreases by a fixed percentage at each expansion, the total cost of these resizings, amortized over all insert and delete operations, is still a constant, independent of the number of entries n and of the number m of operations performed.

For example, consider a table that was created with the minimum possible size and is doubled each time the load ratio exceeds some threshold. If m elements are inserted into that table, the total number of extra re-insertions that occur in all dynamic resizings of the table is at most m−1. In other words, dynamic resizing roughly doubles the cost of each insert or delete operation.

[edit] Incremental resizing

On the other hand, some hash table implementations, notably in real-time systems, cannot pay the price of enlarging the hash table all at once, because it may interrupt time-critical operations. One simple approach is to initially allocate the table with enough space for the expected number of elements and forbid the addition of too many elements. Another useful but more memory-intensive technique is to perform the resizing gradually:

• Allocate the new hash table, but leave the old hash table and check both tables during lookups.
• Each time an insertion is performed, add that element to the new table and also move k elements from the old table to the new table.
• When all elements are removed from the old table, deallocate it.

To ensure that the old table will be completely copied over before the new table itself needs to be enlarged, it's necessary to increase the size of the table by a factor of at least (k + 1)/k during the resizing.

[edit] Other solutions

Linear hashing ^[10] is a hash table algorithm that permits incremental hash table expansion. It is implemented using a single hash table, but with two possible look-up functions.

Another way to decrease the cost of table resizing is to choose a hash function in such a way that the hashes of most values do not change when the table is resized. This approach, called consistent hashing, is prevalent in disk-based and distributed hashes, where resizing is prohibitively costly.

[edit] Choosing a good hash function

A good hash function is essential for good hash table performance. A poor choice of a hash function is likely to lead to clustering.

In which probability of keys mapping to the same hash bucket (i.e. a collision) is significantly greater than would be expected from a random function.

The cost of resolving a collision scales linearly with the number of keys mapping to the same bucket, so excess collisions will degrade performance significantly. In addition, some hash functions are computationally expensive, so the amount of time (and, in some cases, memory) taken to compute the hash may be burdensome.

Choosing a good hash function is tricky. The literature is replete with poor choices, at least when measured by modern standards. For example, the very popular multiplicative hash advocated by Donald Knuth in The Art of Computer Programming (see reference below) has particularly poor clustering behavior. [1]

However, since poor hashing merely degrades hash table performance for particular input key distributions, such problems commonly go undetected.

However, the (presumed) uniformity of the resulting hash value distribution is hardly worth their much larger computational cost and algorithmic complexity. (They may be appropriate, however, to prevent malicious users from sabotaging a netowrk service by submitting requests designed to generate a large number of collisions in the server's hash tables^{[citation needed]}. Even then, other methods (such as applying a secret salt to the data, or using a universal hash function) may be just as effective but much cheaper.

There is no universal consensus on what makes a "good" hash function.

One criterion is uniformity of the distribution of hash values. Bret Mulvey proposes the use of a chi-squared test for uniformity, based on power of two hash table sizes ranging from 2¹ to 2¹⁶. This test is considerably more sensitive than many others proposed for measuring hash functions, and finds problems in many popular hash functions.

One desirable property of a hash function is that conversion from the hash value (typically 32 bits) to a bucket index for a particular-size hash table can be done simply by masking, preserving only the lower k bits for a table of size 2^k (an operation equivalent to computing the hash value modulo the table size). This property enables the technique of incremental doubling of the size of the hash table - each bucket in the old table maps to only two in the new table. Because of its use of XOR-folding, the FNV hash does not have this property. Some older hashes are even worse, requiring table sizes to be a prime number rather than a power of two, again computing the bucket index as the hash value modulo the table size. In general, such a requirement is a sign of a fundamentally weak function; using a prime table size is a poor substitute for using a stronger function.

In the absence of a standard measure for hash function strength, the current state of the art is to employ a battery of statistical tests to measure whether the hash function can be readily distinguished from a random function. Arguably a good cryptograhic hash function should have the avalanche effect, which essentially states that any single-bit change in the input key should affect, on average, half the bits in the output. Bret Mulvey advocates testing the strict avalanche condition in particular, which states that, for any single-bit change, each of the output bits should change with probability one-half, independent of the other bits in the key. Purely additive hash functions such as CRC fail this stronger condition miserably.

[edit] Implementations

While many programming languages already provide hash table functionality (see language support for associative arrays), there are several independent implementations worth mentioning.

• Google Sparse Hash The Google SparseHash project contains several hash-map implementations in use at Google, with different performance characteristics, including an implementation that optimizes for space and one that optimizes for speed. The memory-optimized one is extremely memory-efficient with only 2 bits/entry of overhead.
• SunriseDD An open source C library for hash table storage of arbitrary data objects with lock-free lookups, built-in reference counting and guaranteed order iteration. The library can participate in external reference counting systems or use its own built-in reference counting. It comes with a variety of hash functions and allows the use of runtime supplied hash functions via callback mechanism. Source code is well documented.
• uthash This is an easy-to-use hash table for C structures.
• A number of language runtimes and/or standard libraries use hash tables to implement their support for associative arrays.
• Software written to minimize memory usage can conserve memory by keeping all allocated strings in a hash table. If an already existing string is found a pointer to that string is returned; otherwise, a new string is allocated and added to the hash table. (This is the normal technique used in Lisp for the names of variables and functions; see the documentation for the intern and intern-soft functions if you are using that language.) The data compression achieved in this manner is usually around 40%.^{[citation needed]}

[edit] See also

[edit] References

[edit] Further reading

• Michael T. Goodrich and Roberto Tamassia. Data Structures and Algorithms in Java, 4th edition. John Wiley & Sons, Inc. ISBN 0-471-73884-0. Chapter 9: Maps and Dictionaries. pp.369–418
• Aaron M. Tenenbaum, Yedidyah Langsam, and Moshe J. Augenstein. Data Structures Using C, Prentice Hall ISBN 0-13-199746-7. Chapter 7, Section 7.4 - Hashing. pp.454–502

[edit] External links

Wikimedia Commons has media related to: Hash tables

• A Hash Function for Hash Table Lookup by Bob Jenkins.
• Hash Functions by Bret Mulvey (Pluto Scarab) - with nice graphs
• Hash functions by Paul Hsieh
• Hashtables, Part 2 by Maciej Stachowiak
• Libhashish is one of the most feature rich hash libraries (built-in hash functions, several collision strategies, extensive analysis functionality, ...)
• NIST entry on hash tables
• Open addressing hash table removal algorithm from ICI programming language, ici_set_unassign in set.c (and other occurrences, with permission).
• The Perl Wikibook - Perl Hash Variables
• A basic explanation of how the hash table works by Reliable Software
• Lecture on Hash Tables
• Hash'em all! — free online text and file hashing with different algorithms
• qDecoder's C/C++ dynamic allocatable hash-table implementation — opensource library
• qDecoder's C/C++ static array-based hash-table implementation — opensource library
• Hash-tables in C — two simple and clear examples of hash tables implementation in C with linear probing and chaining
• C Hash Table
• Implementation of HashTable in C
• MIT's Introduction to Algorithms: Hashing 1 MIT OCW lecture Video
• MIT's Introduction to Algorithms: Hashing 2 MIT OCW lecture Video