Soap bubble
From Wikipedia, the free encyclopedia
| This article does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (December 2008) |
A soap bubble is a very thin film of soap water that forms a sphere with an iridescent surface. Soap bubbles usually last for only a few moments before bursting: either on their own or on contact with another object. They are often used for children's enjoyment, but their usage in artistic performances shows that they can be fascinating for adults too. Soap bubbles can help to solve complex mathematical problems of space, as they will always find the smallest surface area between points or edges for example.
Contents |
[edit] Physics
[edit] Surface tension and shape

A soap bubble can exist because the surface layer of a liquid (usually water) has a certain surface tension, which causes the layer to behave somewhat like an elastic sheet. However, a bubble made with a pure liquid alone is not stable and a dissolved surfactant such as soap is needed to stabilize a bubble. A common misconception is that soap increases the water's surface tension, soap actually does the opposite, decreasing it to approximately one third the surface tension of pure water. Soap does not strengthen bubbles, it stabilizes them, via an action known as the Marangoni effect. As the soap film stretches, the surface concentration of soap decreases, which in turn causes the surface tension to increase. So soap selectively strengthens the weakest parts of the bubble and tends to prevent them from stretching further. In addition, the soap reduces evaporation so the bubbles last longer, although this effect is relatively small.
Their spherical shape is also caused by surface tension. The tension causes the bubble to form a sphere, as a sphere has the smallest possible surface area for a given volume. This shape can be visibly distorted by air currents. However, if a bubble is left to sink in still air, it remains very nearly spherical, more so for example than the typical cartoon depiction of a raindrop. When a sinking body has reached its terminal velocity, the drag force acting on it is equal to its weight. Since a bubble's weight is much smaller in relation to its size than a raindrop's, its shape is distorted much less. (The surface tension opposing the distortion is similar in the two cases: The soap reduces the water's surface tension to approximately one third, but it is effectively doubled since the film has an inner and an outer surface.)
[edit] Freezing
Soap bubbles blown into air that is below a temperature of −15 °C (5 °F) will freeze when they touch a surface. The air inside will gradually diffuse out, causing the bubble to crumple under its own weight.
At temperatures below about −25 °C (−13 °F), bubbles will freeze in the air and may shatter when hitting the ground. When a bubble is blown with warm air the bubble will freeze to an almost perfect sphere at first, but when the warm air cools and a reduction in volume occurs there will be a partial collapse of the bubble. A bubble, created successfully at this low temperature, will always be rather small in size: it will freeze quickly and continuing to increase the bubble will shatter it.

[edit] Merging
When two bubbles merge, the same physical principles apply, and the bubbles will adopt the shape with the smallest possible surface area. Their common wall will bulge into the larger bubble, as smaller bubbles have a higher internal pressure (also known as Ostwald ripening which is caused by pressure differences in bubbles of different radii as predicted by the Young–Laplace equation). If the bubbles are of equal size, the wall will be flat.
At a point where three or more bubbles meet, they sort themselves out so that only three bubble walls meet along a line. Since the surface tension is the same in each of the three surfaces, the three angles between them must be equal angles of 120°. This is the most efficient choice, again, which is also the reason why the cells of a beehive use the same 120° angle which forms hexagons. Only four bubble walls can meet at a point, with the lines where triplets of bubble walls meet separated by cos−1(−1/3) ≈ 109.47°.
[edit] Interference and reflection
The iridescent colours of soap bubbles are caused by interfering light waves and are determined by the thickness of the film. They are not the same as rainbow colours but are the same as the colours in an oil slick on a wet road.
As light impinges on the film, some of it is reflected off the outer surface while some of it enters the film and reemerges after being reflected back and forth between the two surfaces. The total reflection observed is determined by the interference of all these reflections. Since each traversal of the film incurs a phase shift proportional to the thickness of the film and inversely proportional to the wavelength, the result of the interference depends on these two quantities. So at a given thickness, interference is constructive for some wavelengths and destructive for others, so that white light impinging on the film is reflected with a hue that changes with thickness.
A change in colour can be observed while the bubble is thinning due to evaporation. Thicker walls cancel out red (longer) wavelengths, causing a blue-green reflection. Later, thinner walls will cancel out yellow (leaving blue light), then green (leaving magenta), then blue (leaving a golden yellow). Finally, when the bubble's wall becomes much thinner than the wavelength of visible light, all the waves in the visible region cancel each other out and no reflection is visible at all. When this state is observed, the wall is thinner than about 25 nanometres, and is probably about to pop. This phenomenon is very useful when making or manipulating bubbles as it gives an indication of the bubble's fragility.
Interference effects also depend upon the angle at which the light strikes the film, an effect called iridescence. So, even if the wall of the bubble were of uniform thickness, one would still see variations of colour due to curvature and/or movement. However, the thickness of the wall is continuously changing as gravity pulls the liquid downwards, so bands of colours that move downwards can usually also be observed.
|
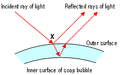
In the diagram above a ray of light hits the surface at point X. Some of the light is reflected, but some travels through the bubble wall and is reflected at the other side.
When light directed from low index material strikes a high index material (air to film), there is a 180 degree phase shift just from the reflection (a "hard" reflection). So the film thicknesses discussed for red and blue light in the panels to the right are incorrect by half a wavelength. |
In this diagram we look at two rays of red light (rays 1 and 2). Both rays are split as before and follow two possible paths, but we are interested only in the paths that are represented by the solid lines. Consider the ray emerging at Y. It consists of two rays on top of one another: the bit that went through the bubble wall for ray 1 and the bit that was reflected off the outer wall of ray 2. Ray one has travelled XOY further than ray 2. Since XOY happens to correspond to an integer multiple of the wavelength of red light, the two rays are in phase (the humps and troughs are together). |
This is similar to the previous diagram except the wavelength is different. This time XOY is not an integer multiple of the wavelength of blue light and so ray 1 and 2 arrive at y out of step. The troughs of ray 1 line up with the humps of ray 2 and the two rays cancel each other out. The overall effect is that no blue light will be reflected for this thickness of bubble. |
[edit] Mathematical aspects of the phenomenon
Soap bubbles are also physical illustrations of the minimal surface problem, a complex mathematical problem. While it has been known since 1884 that a spherical soap bubble is the least-area way of enclosing a given volume of air (a theorem of H. A. Schwarz), it was not until 2000 that it was proven that two merged soap bubbles provide the optimum way of enclosing two given volumes of air with the least surface area. This has been coined the double bubble theorem.
Many bubbles packed together in a foam have much more complicated shapes. See Weaire-Phelan structure for a discussion of this (called the Kelvin problem), and Plateau's laws for a discussion of the structure of the films.
[edit] Coloured bubbles
Adding coloured dye to bubble mixtures fails to produce coloured bubbles, because the dye attaches to the water molecules as opposed to the surfactant. Therefore, a colourless bubble forms with the dye falling to a point at the base. Dye chemist Dr. Ram Sabnis has developed a lactone dye that sticks to the surfactants, enabling brightly coloured bubbles to be formed, crystal violet lactone is an example.
[edit] History of bubbles as playthings
17th century Flemish paintings show children blowing bubbles with clay pipes. This means that bubbles as playthings are at least 400 years old. The London based firm of A. & F. Pears created a famous advertisement campaign for its soaps in 1886 using a painting by Millais of a child playing with bubbles. A Chicago company called Chemtoy began selling bubble solution in the 1940s, and they have captivated children ever since. According to one industry estimate, retailers sell around 200 million bottles annually, perhaps more than any other toy.
[edit] Bubble blowers
Most closed-ring structures will work. A blower can be made by bending a wire into a loop with a handle, where the wire should be thick enough so the ring remains stiff. It can be improved by wrapping a thread or bandages around the wire so the soap water can stick better to the outside rim.
Bubbles can be blown by using a bubble pipe, which is made of plastic and usually takes the shape of a smoking pipe, sometimes containing multiple bowls. The bubble solution is poured into the bowl of the pipe; when someone blows into the mouthpiece, bubbles rise from the bowl.
[edit] Giant bubbles
In 1984 New York architect David Stein invented the Bubble Thing to amuse his young daughter. It uses a very large flexible loop of cotton fabric (and a bucket of soap suds) to create truly enormous spherical bubbles up to eight feet in diameter and tubular bubbles fifty feet long and more. Since 1985 the Bubble Thing has been marketed worldwide by David Stein Inc and Klutz Press.
[edit] Performance art
Soap bubble performances combine entertainment with artistic achievement. They require a high degree of skill as well as perfect bubble suds. Some artists create giant bubbles or tubes, often enveloping objects or even humans. Others manage to create bubbles forming cubes, tetrahedra and other shapes or sculptures. Bubbles are often handled with bare hands. To add to the visual experience, they are sometimes filled with smoke or helium and combined with laser lights or fire. Soap bubbles can be filled with a flammable gas such as natural gas and then ignited. Of course, this destroys the bubble.
[edit] See also
- Joseph Plateau, formulator of Plateau's laws on the geometry of intersecting soap films, and Plateau's problem.
- The French writer Alfred Jarry was highly impressed by physicist C. V. Boys's Soap-Bubbles: Their Colours and the Forces that Mould Them and incorporated parts of it into his eccentric novel Exploits and Opinions of Dr. Faustroll, pataphysician, written in 1898. The book describes the exploits and teachings of a sort of philosopher who, born at age 63, travels through Paris in a sieve and subscribes to the tenets of 'pataphysics, which deals with "the laws which govern exceptions and will explain the universe supplementary to this one". In 'pataphysics, every event in the universe is accepted as an extraordinary event.
- Zubbles, coloured bubbles.
- Antibubble
[edit] References
| Wikimedia Commons has media related to: Soap bubble |
[edit] Further reading
- A more detailed scientific explanation
- The proof paper on the Double Bubble Theorem
- A book about soap bubbles and mathematics: Oprea, John (2000). The Mathematics of Soap Films – Explorations with Maple. American Mathematical Society (1st ed.). ISBN 0-8218-2118-0
- Boys, C. V. (1890) Soap-Bubbles and the Forces that Mould Them; (Dover reprint) ISBN 0-486-20542-8. Classic Victorian exposition, based on a series of lectures originally delivered "before a juvenile audience".
- Isenberg, Cyril (1992) The Science of Soap Films and Soap Bubbles ; (Dover) ISBN 0-486-26960-4.
[edit] External links