Gravitational singularity
From Wikipedia, the free encyclopedia
| General relativity | ||||||||||||
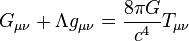 |
||||||||||||
| Einstein field equations | ||||||||||||
| Introduction to... Mathematical formulation of... Resources
|
||||||||||||
A gravitational singularity or spacetime singularity is a location where the quantities which are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system. These quantities are the scalar invariant curvatures of spacetime, some of which are a measure of the density of matter.
For the purposes of proving the Penrose-Hawking singularity theorems, a spacetime with a singularity is defined to be one which contains geodesics which cannot be extended in a smooth manner. The end of such a geodesic is considered to be the singularity. This is a different definition, useful for proving theorems.
The two most important types of spacetime singularities are curvature singularities and conical singularities. Singularities can also be divided according to whether they are covered by an event horizon or not (naked singularities). According to general relativity, the initial state of the universe, at the beginning of the Big Bang, was a singularity. Another type of singularity predicted by general relativity is inside a black hole: any star collapsing beyond a certain point would form a black hole, inside which a singularity (covered by an event horizon) would be formed, as all the matter would flow into a certain point (or a circular line, if the black hole is rotating). These singularities are also known as curvature singularities.
Contents |
[edit] Interpretation
Many theories in physics have mathematical singularities of one kind or another. Equations for these physical theories predict that the rate of change of some quantity becomes infinite or increases without limit. This is generally a sign for a missing piece in the theory, as in the Ultraviolet Catastrophe and in renormalization.
In supersymmetry, a singularity in the moduli space happens usually when there are additional massless degrees of freedom in that certain point. Similarly, it is thought that singularities in spacetime often mean that there are additional degrees of freedom that exist only within the vicinity of the singularity. The same, fields related to the whole spacetime, also exist; for example, the electromagnetic field. In known examples of string theory, the latter degrees of freedom are related to closed strings, while the degrees of freedom are "stuck" to the singularity and related either to open strings or to the twisted sector of an orbifold.
[edit] Types
[edit] Curvature
Solutions to the equations of general relativity or another theory of gravity (such as supergravity), often result in encountering points where the metric blows up to infinity. However, many of these points are in fact completely regular. Moreover, the infinities are merely a result of using an inappropriate coordinate system at this point. Thus, in order to test whether there is a singularity at a certain point, one must check whether at this point diffeomorphism invariant quantities (i.e. scalars) become infinite. Such quantities are the same in every coordinate system, so these infinities will not "go away" by a change of coordinates.
An example is the Schwarzschild solution which describes a non-rotating, uncharged black hole. In coordinate systems convenient for working in regions far away from the black hole, a part of the metric becomes infinite at the event horizon. However, spacetime at the event horizon is regular. The regularity becomes evident when changing to another coordinate system (such as the Kruskal coordinates), where the metric is perfectly smooth. On the other hand, in the center of the black hole, where the metric becomes infinite as well, the solutions suggest singularity exists. The existence of the singularity can be verified by noting that the Kretschmann scalar or square of the Riemann tensor, RμνρσRμνρσ, which is diffeomorphism invariant, is infinite. While in a non-rotating black hole the singularity occurs at a single point in the model coordinates, called a "point singularity", in a rotating black hole, also known as a Kerr black hole, the singularity occurs on a ring (a circular line), defined as a "ring singularity". Such a singularity may also theoretically become a wormhole.[1]
More generally, a spacetime is considered singular if it is geodesically incomplete, meaning that there are freely-falling particles whose motion cannot be determined at a finite time at the point of reaching the singularity. For example, any observer below the event horizon of a nonrotating black hole would fall into its center within a finite period of time. The simplest Big Bang cosmological model of the universe contains a causal singularity at the start of time (t=0), where all timelike geodesics have no extensions into the past. Extrapolating backward to this hypothetical time 0 results in a universe of size 0 in all spatial dimensions, infinite density, infinite temperature, and infinite space-time curvature.
[edit] Conical
A conical singularity occurs when there is a point where the limit of every diffeomorphism invariant quantity is finite. In which case, spacetime is not smooth at the point of the limit itself. Thus, spacetime looks like a cone around this point, where the singularity is located at the tip of the cone. The metric can be finite everywhere if a suitable coordinate system is used.
An example of such a conical singularity is a cosmic string.
[edit] Naked
Until the early 1990s, it was widely believed that general relativity hides every singularity behind an event horizon, making naked singularities impossible. This is referred to as the cosmic censorship hypothesis. However, in 1991 Shapiro and Teukolsky performed computer simulations of a rotating plane of dust which indicated that general relativity might allow for "naked" singularities. What these objects would actually look like in such a model is unknown. Nor is it known whether singularities would still arise if the simplifying assumptions used to make the simulation were removed.
[edit] See also
- Penrose-Hawking singularity theorems
- 0-dimensional singularity: magnetic monopole
- 1-dimensional singularity: cosmic string
- 2-dimensional singularity: domain wall
[edit] Notes
- See the discussion of entropy and Hawking radiation under black hole. Before Stephen Hawking came up with the concept of Hawking radiation, the question of black holes having entropy was avoided. However, this concept demonstrates that black holes can radiate energy, which conserves entropy and solves the incompatibility problems with the second law of thermodynamics. Entropy, however, implies heat and therefore temperature. The loss of energy also suggests that black holes do not last forever, but rather "evaporate" slowly. Small black holes tend to be hotter whereas larger ones tend to be colder. All known black holes are so large that their temperature is far below that of the cosmic background radiation, so they are all gaining energy. They will not begin to lose energy until a cosmological redshift of more than a million is reached, rather than the thousand or so since the background radiation formed.
[edit] Notes and references
- ^ If a rotating singularity is given a uniform electrical charge, a repellent force results, causing a ring singularity to form. The effect may be a stable wormhole, a non-point-like puncture in spacetime which may be connected to a second ring singularity on the other end. Although such wormholes are often suggested as routes for faster-than-light travel, such suggestions ignore the problem of escaping the black hole at the other end, or even of surviving the immense tidal forces in the tightly curved interior of the wormhole.
- Shapiro, Stuart L.; Teukolsky, Saul A. (February 1991). "Formation of naked singularities: The violation of cosmic censorship". Physical Review Letters (American Physical Society) 66 (8): 994–997. doi:. http://link.aps.org/abstract/PRL/v66/p994. Retrieved on 2007-01-18.
- Robert M. Wald (1984). 'General Relativity'. Chicago. ISBN 0-226-87033-2.
- Charles W. Misner; Kip Thorne & John Archibald Wheeler (1973). 'Gravitation'. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0. §31.2 The nonsingularity of the gravitational radius, and following sections; §34 Global Techniques, Horizons, and Singularity Theorems
[edit] Further reading
- The Elegant Universe by Brian Greene. This book provides a layman's introduction to string theory, although some of the views expressed are already becoming outdated. His use of common terms and his providing of examples throughout the text help the layperson understand the basics of string theory.

