Queueing model

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In queueing theory, a queueing model is used to approximate a real queueing situation or system, so the queueing behaviour can be analysed mathematically. Queueing models allow a number of useful steady state performance measures to be determined, including:

  • the average number in the queue, or the system,
  • the average time spent in the queue, or the system,
  • the statistical distribution of those numbers or times,
  • the probability the queue is full, or empty, and
  • the probability of finding the system in a particular state.

These performance measures are important as issues or problems caused by queueing situations are often related to customer dissatisfaction with service or may be the root cause of economic losses in a business. Analysis of the relevant queueing models allows the cause of queueing issues to be identified and the impact of proposed changes to be assessed.

Contents

[edit] Notation

Queuing models can be represented using Kendall's notation:

A/B/S/K/N/Disc

where:

  • A is the interarrival time distribution
  • B is the service time distribution
  • S is the number of servers
  • K is the system capacity
  • N is the calling population
  • Disc is the service discipline assumed

Many times the last members are omitted, so the notation becomes A/B/S and it is assumed that K = {\infty}, N = {\infty} and Disc = FIFO.

Some standard notation for distributions (A or B) are:

[edit] Models

[edit] Construction and analysis

Queueing models are generally constructed to represent the steady state of a queueing system, that is, the typical, long run or average state of the system. As a consequence, these are stochastic models that represent the probability that a queueing system will be found in a particular configuration or state.

A general procedure for constructing and analysing such queueing models is:

  1. Identify the parameters of the system, such as the arrival rate, service time, queue capacity, and perhaps draw a diagram of the system.
  2. Identify the system states. (A state will generally represent the integer number of customers, people, jobs, calls, messages, etc. in the system and may or may not be limited.)
  3. Draw a state transition diagram that represents the possible system states and identify the rates to enter and leave each state. This diagram is a representation of a Markov chain.
  4. Because the state transition diagram represents the steady state situation between state there is a balanced flow between states so the probabilities of being in adjacent states can be related mathematically in terms of the arrival and service rates and state probabilities.
  5. Express all the state probabilities in terms of the empty state probability, using the inter-state transition relationships.
  6. Determine the empty state probability by using the fact that all state probabilities always sum to 1.

Whereas specific problems that have small finite state models can often be analysed numerically, analysis of more general models, using calculus, yields useful formulae that can be applied to whole classes of problems.

[edit] Single-server queue

Single-server queues are, perhaps, the most commonly encountered queueing situation in real life. One encounters a queue with a single server in many situations, including business (e.g. sales clerk), industry (e.g. a production line), transport (e.g. a bus, a taxi rank, an intersection), telecommunications (e.g. Telephone line), computing (e.g. processor sharing). Even where there are multiple servers handling the situation it is possible to consider each server individually as part of the larger system, in many cases. (e.g A supermarket checkout has several single server queues that the customer can select from.) Consequently, being able to model and analyse a single server queue's behaviour is a particularly useful thing to do.

[edit] Poisson arrivals and service

M/M/1/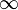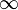\infty/\infty represents a single server that has unlimited queue capacity and infinite calling population, both arrivals and service are Poisson (or random) processes, meaning the statistical distribution of both the inter-arrival times and the service times follow the exponential distribution. Because of the mathematical nature of the exponential distribution, a number of quite simple relationships are able to be derived for several performance measures based on knowing the arrival rate and service rate.

This is fortunate because, an M/M/1 queuing model can be used to approximate many queuing situations.

[edit] Poisson arrivals and general service

M/G/1/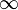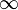\infty/\infty represents a single server that has unlimited queue capacity and infinite calling population, while the arrival is still Poisson process, meaning the statistical distribution of the inter-arrival times still follow the exponential distribution, the distribution of the service time does not. The distribution of the service time may follow any general statistical distribution, not just exponential. Relationships are still able to be derived for a (limited) number of performance measures if one knows the arrival rate and the mean and variance of the service rate. However the derivations are generally more complex

A number of special cases of M/G/1 provide specific solutions that give broad insights into the best model to choose for specific queueing situations because they permit the comparison of those solutions to the performance of an M/M/1 model.

[edit] Multiple-servers queue

Multiple (identical)-servers queue situations are frequently encountered in telecommunications or a customer service environment. When modelling these situations care is needed to ensure that it is a multiple servers queue, not a network of single server queues, because results may differ depending on how the queuing model behaves.

One observational insight provided by comparing queuing models is that a single queue with multiple servers performs better than each server having their own queue and that a single large pool of servers performs better than two or more smaller pools, even though there are the same total number of servers in the system.

One simple example to prove the above fact is as follows: Consider a system having 8 input lines, single queue and 8 servers.The output line has a capacity of 64 kbit/s. Considering the arrival rate at each input as 2 packets/s. So, the total arrival rate is 16 packets/s. With an average of 2000 bits per packet, the service rate is 64 kbit/s/2000b = 32 packets/s. Hence, the average response time of the system is 1/(μ − λ) = 1/(32 − 16) = 0.0625 sec. Now, consider a second system with 8 queues, one for each server. Each of the 8 output lines has a capacity of 8 kbit/s. The calculation yields the response time as 1/(μ − λ) = 1/(4 − 2) = 0.5 sec. And the average waiting time in the queue in the first case is ρ/(1 − ρ)μ = 0.03125, while in the second case is 0.25.

[edit] Infinitely many servers

While never exactly encountered in reality, an infinite-servers (e.g. M/M/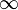\infty) model is a convenient theoretical model for situations that involve storage or delay, such as parking lots, warehouses and even atomic transitions. In these models there is no queue, as such, instead each arriving customer receives service. When viewed from the outside, the model appears to delay or store each customer for some time.

[edit] See also

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Queueing_model"
Personal tools