Gibbs sampling

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In mathematics and physics, Gibbs sampling is an algorithm to generate a sequence of samples from the joint probability distribution of two or more random variables. The purpose of such a sequence is to approximate the joint distribution, or to compute an integral (such as an expected value). Gibbs sampling is a special case of the Metropolis-Hastings algorithm, and thus an example of a Markov chain Monte Carlo algorithm. The algorithm is named after the physicist J. W. Gibbs, in reference to an analogy between the sampling algorithm and statistical physics. The algorithm was devised by Stuart Geman and Donald Geman, some eight decades after the passing of Gibbs, and is also called the Gibbs sampler.[1]

Gibbs sampling is applicable when the joint distribution is not known explicitly, but the conditional distribution of each variable is known. The Gibbs sampling algorithm generates an instance from the distribution of each variable in turn, conditional on the current values of the other variables. It can be shown (see, for example, Gelman et al. 1995) that the sequence of samples constitutes a Markov chain, and the stationary distribution of that Markov chain is just the sought-after joint distribution.

Gibbs sampling is particularly well-adapted to sampling the posterior distribution of a Bayesian network, since Bayesian networks are typically specified as a collection of conditional distributions. BUGS (link below) is a program for carrying out Gibbs sampling on Bayesian networks.

Contents

[edit] Background

Gibbs sampling is a special case of Metropolis-Hastings sampling. The point of Gibbs sampling is that given a multivariate distribution it is simpler to sample from a conditional distribution than to integrate over a joint distribution. Suppose we want to sample 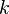\left.k\right. values of \left.x\right. from a joint distribution \left.p(x, y)\right.. We begin with a value of \left.y_0\right. and sample \left.x\right. by x_i \sim p\left(x | y = y_{i-1}\right). Once that value of \left.x\right. is calculated, repeat by sampling for the next \left.y\right.: y_i \sim p\left(y | x = x_i\right).

[edit] Implementation

Suppose that a sample 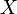\left.X\right. is taken from a distribution depending on a parameter vector 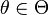\theta \in \Theta \,\! of length 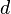\left.d\right., with prior distribution 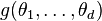g(\theta_1, \ldots , \theta_d). It may be that 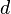\left.d\right. is very large and that numerical integration to find the marginal densities of the 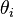\left.\theta_i\right. would be computationally expensive. Then an alternative method of calculating the marginal densities is to create a Markov chain on the space 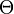\left.\Theta\right. by repeating these two steps:

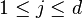
  1. Pick a random index 1 \leq j \leq d
  2. Pick a new value for 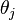\left.\theta_j\right. according to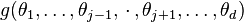 g(\theta_1, \ldots , \theta_{j-1} , \, \cdot \, , \theta_{j+1} , \ldots , \theta_d )

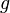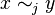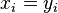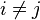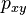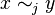These steps define a reversible Markov chain with the desired invariant distribution \left.g\right.. This can be proved as follows. Define x \sim_j y if \left.x_i = y_i\right. for all i \neq j and let \left.p_{xy}\right. denote the probability of a jump from x \in \Theta to y \in \Theta. Then, for x \sim_j y the transition probabilities are

p_{xy} = \frac{1}{d}\frac{g(y)}{\sum_{z \in \Theta: z \sim_j x} g(z) }

and \left.p_{xy} = 0\right. otherwise. So

g(x) p_{xy} = \frac{1}{d}\frac{ g(x) g(y)}{\sum_{z \in \Theta: z \sim_j x} g(z) } = \frac{1}{d}\frac{ g(y) g(x)}{\sum_{z \in \Theta: z \sim_j y} g(z) } = g(y) p_{yx}

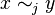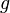since x \sim_j y is an equivalence relation. Thus the detailed balance equations are satisfied, implying the chain is reversible and it has invariant distribution \left.g\right..

In practice, the suffix \left.j\right. is not chosen at random, and the chain cycles through the suffixes in order. In general this gives a non-reversible chain, but it will still have the desired invariant distribution (as long as the chain can access all states under the fixed ordering).

[edit] Failure Modes

There are two ways that Gibbs sampling can fail. The first is when there are islands of high-probability states, with no paths between them. For example, consider a probability distribution over 2-bit vectors, where the vectors (0,0) and (1,1) each have probability 1/2, but the other two vectors (0,1) and (1,0) have probability zero. Gibbs sampling will become trapped in one of the two high-probability vectors, and will never reach the other one. More generally, for any distribution over high-dimensional, real-valued vectors, if 2 particular elements of the vector are perfectly correlated (or perfectly anti-correleated), those 2 elements will become stuck, and Gibbs sampling will never be able to change them.

The second problem can happen even when all states have nonzero probability and there is only a single island of high-probability states. For example, consider a probability distribution over 100-bit vectors, where the all-zeros vector occurs with probability 1/2, and all other vectors are equally probable, and so have a probability of \frac{1}{2(2^{100}-1)} each. If you want to know the probability of the zero vector, it would be sufficient to take 100 or 1000 samples from the true distribution. That would very likely give an answer very close to 1/2. But you would probably have to take more than 2100 samples from Gibbs sampling to get the same result. No computer could do this in a lifetime.

This problem occurs no matter how long the burn in period is. This is because in the true distribution, the zero vector occurs half the time, and those occurrences are randomly mixed in with the nonzero vectors. Even a small sample will see both zero and nonzero vectors. But Gibbs sampling will alternate between returning only the zero vector for long periods (about 299 in a row), then only nonzero vectors for long periods (about 299 in a row). Thus convergence to the true distribution is extremely slow, requiring much more than 299 steps; taking this many steps is not computationally feasible in a reasonable time period. The slow convergence here can be seen as a consequence of the curse of dimensionality.

[edit] See also

[edit] References

  1. ^ S. Geman and Donald Geman (1984). "Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images". IEEE Transactions on Pattern Analysis and Machine Intelligence 6: 721–741. 

[edit] Others

  • George Casella and Edward I. George. "Explaining the Gibbs sampler". The American Statistician, 46:167-174, 1992. (Basic summary and many references.)
  • A.E. Gelfand and A.F.M. Smith. "Sampling-Based Approaches to Calculating Marginal Densities". J. American Statistical Association, 85:398-409, 1990.
  • Andrew Gelman, John B. Carlin, Hal S. Stern, and Donald B. Rubin. Bayesian Data Analysis. London: Chapman and Hall. First edition, 1995. (See Chapter 11.)
  • C.P. Robert and G. Casella. "Monte Carlo Statistical Methods" (second edition). New York: Springer-Verlag, 2004.

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Gibbs_sampling"
Personal tools