Irrational number
From Wikipedia, the free encyclopedia
In mathematics, an irrational number is any real number that is not a rational number—that is, it is a number which cannot be expressed as a fraction m/n, where m and n are integers, with n non-zero. Informally, this means numbers that cannot be represented as simple fractions. It can be deduced that they also cannot be represented as terminating or repeating decimals, but the idea is more profound than that. As a consequence of Cantor's proof that the real numbers are uncountable (and the rationals countable) it follows that almost all real numbers are irrational.[1] Perhaps the best-known irrational numbers are π, e and √2.[2][3][4]
When the ratio of lengths of two line segments is irrational, the line segments are also described as being incommensurable, meaning they share no measure in common. A measure of a line segment I in this sense is a line segment J that "measures" I in the sense that some whole number of copies of J laid end-to-end occupy the same length as I.
Contents |
[edit] History
The concept of irrationality was implicitly accepted by Indian mathematicians since the 7th century BC, when Manava (c. 750–690 BC) was aware that the square roots of certain numbers such as 2 and 61 could not be exactly determined.[5]
The first proof of the existence of irrational numbers is usually attributed to Hippasus of Metapontum,[6] a Pythagorean who probably discovered them while identifying sides of the pentagram.[7] The then-current Pythagorean method would have claimed that there must be some sufficiently small, indivisible unit that could fit evenly into one of these lengths as well as the other. However, Hippasus, in the 5th century BC, was able to deduce that there was in fact no common unit of measure, and that the assertion of such an existence was in fact a contradiction. He did this by demonstrating that if the hypotenuse of an isosceles right triangle was indeed commensurable with an arm, then that unit of measure must be both odd and even, which is impossible. His reasoning is as follows:
-
- The ratio of the hypotenuse to an arm of an isosceles right triangle is a:b expressed in the smallest units possible.
- By the Pythagorean theorem: a2 = 2b2.
- Since a2 is even, a must be even as the square of an odd number is odd.
- Since a:b is in its lowest terms, b must be odd.
- Since a is even, let a = 2y.
- Then a2 = 4y2 = 2b2
- b2 = 2y2 so b2 must be even, therefore b is even.
- However we asserted b must be odd. Here is the contradiction.[8]
Greek mathematicians termed this ratio of incommensurable magnitudes alogos, or inexpressible. Hippasus, however, was not lauded for his efforts: according to one legend, he made his discovery while out at sea, and was subsequently thrown overboard by his fellow Pythagoreans “…for having produced an element in the universe which denied the…doctrine that all phenomena in the universe can be reduced to whole numbers and their ratios.”[9] Another legend states that Hippasus was merely exiled for this revelation. Whatever the consequence to Hippasus himself, his discovery posed a very serious problem to Pythagorean mathematics, since it shattered the assumption that number and geometry were inseparable--a foundation of their theory.
Theodorus of Cyrene proved the irrationality of the surds of whole numbers up to 17, but stopped there probably because the algebra he used couldn't be applied to the square root of 17.[10] It wasn't until Eudoxus developed a theory of proportion that took into account irrational as well as rational ratios that a strong mathematical foundation of irrational numbers was created.[11] A magnitude “was not a number but stood for entities such as line segments, angles, areas, volumes, and time which could vary, as we would say, continuously. Magnitudes were opposed to numbers, which jumped from one value to another, as from 4 to 5.”[12] Numbers are composed of some smallest, indivisible unit, whereas magnitudes are infinitely reducible. Because no quantitative values were assigned to magnitudes, Eudoxus was then able to account for both commensurable and incommensurable ratios by defining a ratio in terms of its magnitude, and proportion as an equality between two ratios. By taking quantitative values (numbers) out of the equation, he avoided the trap of having to express an irrational number as a number. “Eudoxus’ theory enabled the Greek mathematicians to make tremendous progress in geometry by supplying the necessary logical foundation for incommensurable ratios.”[13] Euclid's Elements Book 10 is dedicated to classification of irrational magnitudes.
[edit] Middle Ages
The Middle Ages saw the acceptance of zero, negative, integral and fractional numbers, first by Indian and Chinese mathematicians, and then by Arabic mathematicians, who were also the first to treat irrational numbers as algebraic objects,[14] which was made possible by the development of algebra. Arabic mathematicians also merged the concepts of "number" and "magnitude" into a more general idea of real numbers, and they criticized Euclid's idea of ratios, developed the theory of composite ratios, and extended the concept of number to ratios of continuous magnitude.[15] In his commentary on Book 10 of the Elements, the Persian mathematician Al-Mahani (d. 874/884) examined and classified quadratic irrationals and cubic irrationals. He provided definitions for rational and irrational magnitudes, which he treated as irrational numbers. He dealt with them freely but explains them in geometric terms as follows:[16]
"It will be a rational (magnitude) when we, for instance, say 10, 12, 3%, 6%, etc., because its value is pronounced and expressed quantitatively. What is not rational is irrational and it is impossible to pronounce and represent its value quantitatively. For example: the roots of numbers such as 10, 15, 20 which are not squares, the sides of numbers which are not cubes etc."
In contrast to Euclid's concept of magnitudes as lines, Al-Mahani considered integers and fractions as rational magnitudes, and square roots and cube roots as irrational magnitudes. He also introduced an arithmetical approach to the concept of irrationality, as he attributes the following to irrational magnitudes:[16]
"their sums or differences, or results of their addition to a rational magnitude, or results of subtracting a magnitude of this kind from an irrational one, or of a rational magnitude from it."
The Egyptian mathematician Abū Kāmil Shujā ibn Aslam (c. 850–930) was the first to accept irrational numbers as solutions to quadratic equations or as coefficients in an equation, often in the form of square roots, cube roots and fourth roots.[17] In the 10th century, the Iraqi mathematician Al-Hashimi provided general proofs (rather than geometric demonstrations) for irrational numbers, as he considered multiplication, division, and other arithmetical functions.[18] Abū Ja'far al-Khāzin (900-971) provides a definition of rational and irrational magnitudes, stating that if a definite quantity is:[19]
"contained in a certain given magnitude once or many times, then this (given) magnitude corresponds to a rational number. . . . Each time when this (latter) magnitude comprises a half, or a third, or a quarter of the given magnitude (of the unit), or, compared with (the unit), comprises three, five, or three fifths, it is a rational magnitude. And, in general, each magnitude that corresponds to this magnitude (i.e. to the unit), as one number to another, is rational. If, however, a magnitude cannot be represented as a multiple, a part (l/n), or parts (m/n) of a given magnitude, it is irrational, i.e. it cannot be expressed other than by means of roots."
Many of these concepts were eventually accepted by European mathematicians sometime after the Latin translations of the 12th century. Al-Hassār, an Arabic mathematician from the Maghreb (North Africa) specializing in Islamic inheritance jurisprudence during the 12th century, developed the modern symbolic mathematical notation for fractions, where the numerator and denominator are separated by a horizontal bar. This same fractional notation appears soon after in the work of Fibonacci in the 13th century.[20] During the 14th to 16th centuries, Madhava of Sangamagrama and the Kerala school of astronomy and mathematics discovered the infinite series for several irrational numbers such as pi and certain irrational values of trigonometric functions. Jyesthadeva provided proofs for these infinite series in the Yuktibhasa.[21]
[edit] Modern period
The 17th century saw imaginary numbers become a powerful tool in the hands of Abraham de Moivre, and especially of Leonhard Euler. The completion of the theory of complex numbers in the nineteenth century entailed the differentiation of irrationals into algebraic and transcendental numbers, the proof of the existence of transcendental numbers, and the resurgence of the scientific study of the theory of irrationals, largely ignored since Euclid. The year 1872 saw the publication of the theories of Karl Weierstrass (by his pupil Kossak), Heine (Crelle, 74), Georg Cantor (Annalen, 5), and Richard Dedekind. Méray had taken in 1869 the same point of departure as Heine, but the theory is generally referred to the year 1872. Weierstrass's method has been completely set forth by Salvatore Pincherle in 1880,[22] and Dedekind's has received additional prominence through the author's later work (1888) and the recent endorsement by Paul Tannery (1894). Weierstrass, Cantor, and Heine base their theories on infinite series, while Dedekind founds his on the idea of a cut (Schnitt) in the system of real numbers, separating all rational numbers into two groups having certain characteristic properties. The subject has received later contributions at the hands of Weierstrass, Kronecker (Crelle, 101), and Méray.
Continued fractions, closely related to irrational numbers (and due to Cataldi, 1613), received attention at the hands of Euler, and at the opening of the nineteenth century were brought into prominence through the writings of Lagrange. Dirichlet also added to the general theory, as have numerous contributors to the applications of the subject.
Lambert proved (1761) that π cannot be rational, and that en is irrational if n is rational (unless n = 0).[23] While Lambert's proof is often said to be incomplete, modern assessments support it as satisfactory, and in fact for its time it is unusually rigorous. Legendre (1794), after introducing the Bessel-Clifford function, provided a proof to show that π2 is irrational, whence it follows immediately that π is irrational also. The existence of transcendental numbers was first established by Liouville (1844, 1851). Later, Georg Cantor (1873) proved their existence by a different method, that showed that every interval in the reals contains transcendental numbers. Charles Hermite (1873) first proved e transcendental, and Ferdinand von Lindemann (1882), starting from Hermite's conclusions, showed the same for π. Lindemann's proof was much simplified by Weierstrass (1885), still further by David Hilbert (1893), and was finally made elementary by Adolf Hurwitz and Paul Albert Gordan.
[edit] Example proofs
[edit] Square roots
The square root of 2 was the first number to be proved irrational and that article contains a number of proofs. The golden ratio is the next most famous quadratic irrational and there is a simple proof of its irrationality in its article. The square root of all non-square natural numbers is irrational and a proof may be found in quadratic irrationals.
The irrationality of the square root of 2 may be proved by assuming it is rational and inferring a contradiction, called an argument by reductio ad absurdum. The following argument appeals twice to the fact that the square of an odd integer is always odd.
If √2 is rational it has the form m/n for integers m, n not both even. Then m2 = 2n2 whence m is even, say m = 2p. Thus 4p2 = 2n2 so 2p2 = n2 whence n is also even, a contradiction.
[edit] General roots
The proof above for the square root of two can be generalized using the fundamental theorem of arithmetic which was proved by Gauss in 1798. This asserts that every integer has a unique factorization into primes. Using it we can show that if a rational number is not an integer then no integral power of it can be an integer, as in lowest terms there must be a prime in the denominator which does not divide into the numerator whatever power each is raised to. Therefore if an integer is not an exact kth power of another integer then its kth root is irrational.
[edit] Logarithms
Perhaps the numbers most easily proved to be irrational are certain logarithms. Here is a proof by reductio ad absurdum that log2 3 is irrational:
Assume log2 3 is rational. For some positive integers m and n, we have
It follows that
However, 2 to any integer power greater than 0 is even (because at least one of its prime factors is 2) and 3 to any integer power greater than 0 is odd (because none of its prime factors is 2), so the original assumption is false.
Cases such as log10 2 can be treated similarly.
[edit] Transcendental and algebraic irrationals
Almost all irrational numbers are transcendental and all transcendental numbers are irrational: the article on transcendental numbers lists several examples. e r and π r are irrational if r ≠ 0 is rational; eπ is irrational.
Another way to construct irrational numbers is as irrational algebraic numbers, i.e. as zeros of polynomials with integer coefficients: start with a polynomial equation
- p(x) = an xn + an−1 xn−1 + ... + a1 x + a0 = 0
where the coefficients ai are integers. Suppose you know that there exists some real number x with p(x) = 0 (for instance if n is odd and an is non-zero, then because of the intermediate value theorem). The only possible rational roots of this polynomial equation are of the form r/s where r is a divisor of a0 and s is a divisor of an; there are only finitely many such candidates which you can all check by hand. If neither of them is a root of p, then x must be irrational. For example, this technique can be used to show that x = (21/2 + 1)1/3 is irrational: we have (x3 − 1)2 = 2 and hence x6 − 2x3 − 1 = 0, and this latter polynomial does not have any rational roots (the only candidates to check are ±1).
Because the algebraic numbers form a field, many irrational numbers can be constructed by combining transcendental and algebraic numbers. For example 3π + 2, π + √2 and e√3 are irrational (and even transcendental).
[edit] Decimal expansions
The decimal expansion of an irrational number never repeats or terminates, unlike a rational number.
To show this, suppose we divide integers n by m (where m is nonzero). When long division is applied to the division of n by m, only m remainders are possible. If 0 appears as a remainder, the decimal expansion terminates. If 0 never occurs, then the algorithm can run at most m − 1 steps without using any remainder more than once. After that, a remainder must recur, and then the decimal expansion repeats.
Conversely, suppose we are faced with a recurring decimal, we can prove that it is a fraction of two integers. For example:
Here the length of the repitend is 3. We multiply by 103:
Note that since we multiplied by 10 to the power of the length of the repeating part, we shifted the digits to the left of the decimal point by exactly that many positions. Therefore, the tail end of 1000A matches the tail end of A exactly. Here, both 1000A and A have repeating 162 at the end.
Therefore, when we subtract A from both sides, the tail end of 1000A cancels out of the tail end of A:
Then
(135 is the greatest common divisor of 7155 and 9990). Alternatively, since 0.5 = 1/2, one can clear fractions by multiplying the numerator and denominator by 2:
(27 is the greatest common divisor of 1431 and 1998).
The bottom line, 53/74 is a quotient of integers and therefore a rational number.
[edit] Miscellaneous
Here is a famous pure existence or non-constructive proof:
It has been shown that there exist two irrational numbers a and b, such that ab is rational. If √2√2 is rational, then take a = b = √2. Otherwise, take a to be the irrational number √2√2 and b = √2. Then ab = (√2√2)√2 = √2√2·√2 = √22 = 2 which is rational.
√2√2 is transcendental because of the Gelfond–Schneider theorem.
[edit] Open questions
It is not known whether π + e or π − e is irrational or not. In fact, there is no pair of non-zero integers m and n for which it is known whether mπ + ne is irrational or not. Moreover, it is not known whether the set {π, e} is algebraically independent over Q.
It is not known whether 2e, πe, π√2, Catalan's constant, or the Euler-Mascheroni gamma constant γ are irrational.
[edit] The set of all irrationals
Since the reals form an uncountable set, of which the rationals are a countable subset, the complementary set of irrationals is uncountable.
Under the usual (Euclidean) distance function d(x, y) = |x − y|, the real numbers are a metric space and hence also a topological space. Restricting the Euclidean distance function gives the irrationals the structure of a metric space. Since the subspace of irrationals is not closed, the induced metric is not complete. However, being a G-delta set—i.e., a countable intersection of open subsets—in a complete metric space, the space of irrationals is topologically complete: that is, there is a metric on the irrationals inducing the same topology as the restriction of the Euclidean metric, but with respect to which the irrationals are complete. One can see this without knowing the aforementioned fact about G-delta sets: the continued fraction expansion of an irrational number defines a homeomorphism from the space of irrationals to the space of all sequences of positive integers, which is easily seen to be completely metrizable.
Furthermore, the set of all irrationals is a disconnected metric space.
[edit] See also
- Dedekind cut
- Proof that e is irrational
- Proof that π is irrational
- Trigonometric number
- nth root
- Square root of 3
- Rational numbers
[edit] References
- ^ Cantor, Georg (1955, 1915). Contributions to the Founding of the Theory of Transfinite Numbers. New York: Dover. ISBN 978-0486600451.
- ^ The 15 Most Famous Transcendental Numbers. by Clifford A. Pickover. URL retrieved 24 October 2007.
- ^ http://www.mathsisfun.com/irrational-numbers.html; URL retrieved 24 October 2007.
- ^ Eric W. Weisstein, Irrational Number at MathWorld. URL retrieved 26 October 2007.
- ^ T. K. Puttaswamy, "The Accomplishments of Ancient Indian Mathematicians", pp. 411–2, in Selin, Helaine; D'Ambrosio, Ubiratan (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 1402002602.
- ^ Kurt Von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics.
- ^ James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal..
- ^ Kline, M. (1990). Mathematical Thought from Ancient to Modern Times, Vol. 1. New York: Oxford University Press. (Original work published 1972). p.33.
- ^ Kline 1990, p. 32.
- ^ Robert L. McCabe (1976). "Theodorus' Irrationality Proofs". Mathematics Magazine..
- ^ Charles H. Edwards (1982). The historical development of the calculus. Springer.
- ^ Kline 1990, p.48.
- ^ Kline 1990, p.49.
- ^ O'Connor, John J.; Robertson, Edmund F., "Arabic mathematics: forgotten brilliance?", MacTutor History of Mathematics archive.
- ^ Matvievskaya, Galina (1987), "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics", Annals of the New York Academy of Sciences 500: 253-277 [254].
- ^ a b Matvievskaya, Galina (1987), "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics", Annals of the New York Academy of Sciences 500: 253-277 [259].
- ^ Jacques Sesiano, "Islamic mathematics", p. 148, in Selin, Helaine; D'Ambrosio, Ubiratan (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 1402002602.
- ^ Matvievskaya, Galina (1987), "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics", Annals of the New York Academy of Sciences 500: 253-277 [260].
- ^ Matvievskaya, Galina (1987), "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics", Annals of the New York Academy of Sciences 500: 253-277 [261].
- ^ Prof. Ahmed Djebbar (June 2008). "Mathematics in the Medieval Maghrib: General Survey on Mathematical Activities in North Africa". FSTC Limited. http://muslimheritage.com/topics/default.cfm?ArticleID=952. Retrieved on 2008-07-19.
- ^ Katz, V. J. (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine (Mathematical Association of America) 68 (3): 163–74.
- ^ Salvatore Pincherle (1880). "Saggio di una introduzione alla teorica delle funzioni analitiche secondo i principi del prof. Weierstrass". Giornale di Matematiche.
- ^ J. H. Lambert (1761). "Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques". Histoire de l'Académie Royale des Sciences et des Belles-Lettres der Berlin: 265–276.
[edit] Further reading
- Adrien-Marie Legendre, Éléments de Géometrie, Note IV, (1802), Paris
- Rolf Wallisser, "On Lambert's proof of the irrationality of π", in Algebraic Number Theory and Diophantine Analysis, Franz Halter-Koch and Robert F. Tichy, (2000), Walter de Gruyer
[edit] External links
|
|||||||||||

 is irrational.
is irrational.








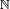 )
) )
) )
)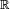 )
) )
)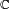 )
) )
) )
)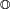 )
) )
)
