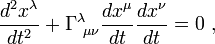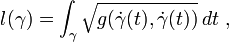Geodesic

From Wikipedia, the free encyclopedia

Jump to: navigation, search
 It has been suggested that geodesic (general relativity) be merged into this article or section. (Discuss)
A geodesic triangle on the sphere. The geodesics are great circle arcs.

In mathematics, a geodesic /ˌdʒiəˈdɛsɪk, -ˈdisɪk/[jee-uh-des-ik, -dee-sik] is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a metric, geodesics are defined to be (locally) the shortest path between points on the space. In the presence of an affine connection, geodesics are defined to be curves whose tangent vectors remain parallel if they are transported along it.

The term "geodesic" comes from geodesy, the science of measuring the size and shape of Earth; in the original sense, a geodesic was the shortest route between two points on the Earth's surface, namely, a segment of a great circle. The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.

Geodesics are of particular importance in general relativity, as they describe the motion of inertial test particles.

Contents

[edit] Introduction

The shortest path between two points in a curved space can be found by writing the equation for the length of a curve (a function f from an open interval of R to the manifold), and then minimizing this length using the calculus of variations. This has some minor technical problems, because there is an infinite dimensional space of different ways to parametrize the shortest path. It is simpler to demand not only that the curve locally minimize length but also that it is parametrized "with constant velocity", meaning that the distance from f(s) to f(t) along the geodesic is proportional to |s−t|. Equivalently, a different quantity may be defined, termed the energy of the curve; minimizing the energy leads to the same equations for a "constant velocity" geodesic. Intuitively, one can understand this second formulation by noting that an elastic band stretched between two points will contract its length, and in so doing will minimize its energy; the resulting shape of the band is a geodesic.

In Riemannian geometry geodesics are not the same as "shortest curves" between two points, though the two concepts are closely related. The difference is that geodesics are only locally the shortest distance between points, and are parametrized with "constant velocity". Going the "long way round" on a great circle between two points on a sphere is a geodesic but not the shortest path between the points. The map t→t2 from the unit interval to itself gives the shortest path between 0 and 1, but is not a geodesic because the velocity of the corresponding motion of a point is not constant.

Geodesics are commonly seen in the study of Riemannian geometry and more generally metric geometry. In relativistic physics, geodesics describe the motion of point particles under the influence of gravity alone. In particular, the path taken by a falling rock, an orbiting satellite, or the shape of a planetary orbit are all geodesics in curved space-time. More generally, the topic of sub-Riemannian geometry deals with the paths that objects may take when they are not free, and their movement is constrained in various ways.

This article presents the mathematical formalism involved in defining, finding, and proving the existence of geodesics, in the case of Riemannian and pseudo-Riemannian manifolds. The article geodesic (general relativity) discusses the special case of general relativity in greater detail.

[edit] Examples

The most familiar examples are the straight lines in Euclidean geometry. On a sphere, the images of geodesics are the great circles. The shortest path from point A to point B on a sphere is given by the shorter piece of the great circle passing through A and B. If A and B are antipodal points (like the North pole and the South pole), then there are infinitely many shortest paths between them.

[edit] Metric geometry

In metric geometry, a geodesic is a curve which is everywhere locally a distance minimizer. More precisely, a curve γ: I → M from an interval I of the reals to the metric space M is a geodesic if there is a constant v ≥ 0 such that for any t ∈ I there is a neighborhood J of t in I such that for any t1, t2 ∈ J we have

d(\gamma(t_1),\gamma(t_2))=v|t_1-t_2|.\,

This generalizes the notion of geodesic for Riemannian manifolds. However, in metric geometry the geodesic considered is often equipped with natural parametrization, i.e. in the above identity v = 1 and

d(\gamma(t_1),\gamma(t_2))=|t_1-t_2|.\,

If the last equality is satisfied for all t1, t2 ∈I, the geodesic is called a minimizing geodesic or shortest path.

In general, a metric space may have no geodesics, except constant curves. At the other extreme, any two points in a length metric space are joined by a minimizing sequence of rectifiable paths, although this minimizing sequence need not converge to a geodesic.

[edit] (Pseudo-)Riemannian geometry

A geodesic on a smooth manifold M with an affine connection ∇ is defined as a curve γ(t) such that parallel transport along the curve preserves the tangent vector to the curve, so

\nabla_{\dot\gamma} \dot\gamma= 0

at each point along the curve, where \dot\gamma is the derivative with respect to t.

Using local coordinates on M, we can write the geodesic equation (using the summation convention) as

\frac{d^2x^\lambda }{dt^2} + \Gamma^{\lambda}_{~\mu \nu }\frac{dx^\mu }{dt}\frac{dx^\nu }{dt} = 0\ ,

where xμ(t) are the coordinates of the curve γ(t) and \Gamma^{\lambda }_{~\mu \nu } are the Christoffel symbols of the connection ∇. This is just an ordinary differential equation for the coordinates. It has a unique solution, given an initial position and an initial velocity. Therefore, from the point of view of classical mechanics, geodesics can be thought of as trajectories of free particles in a manifold.Indeed, the equation \nabla_{\dot\gamma} \dot\gamma= 0 means that the acceleration of the curve has no components in the direction of the surface (and therefore it is perpendicular to the tangent plane of the surface at each point of the curve). So, the motion is completely determinded by the bending of the surface. This is also the idea of the general relativity where particles move on geodesics and the bending is caused by the gravity.

Geodesics for a (pseudo-)Riemannian manifold M are defined to be geodesics for its Levi-Civita connection. In a Riemannian manifold a geodesic is the same as a curve that locally minimizes the length

l(\gamma)=\int_\gamma \sqrt{ g(\dot\gamma(t),\dot\gamma(t)) }\,dt\ ,

and is parametrized so that the tangent vector has constant length. Geodesics can also be defined as extremal curves for the following action energy functional

S(\gamma)=\frac{1}{2}\int g(\dot\gamma(t),\dot\gamma(t))\,dt,

where g is a Riemannian (or pseudo-Riemannian) metric. In pure mathematics, this quantity would generally be referred to as an energy. The geodesic equation can then be obtained as the Euler–Lagrange equations of motion for this action.

In a similar manner, one can obtain geodesics as a solution of the Hamilton–Jacobi equations, with (pseudo-)Riemannian metric taken as Hamiltonian. See Riemannian manifolds in Hamiltonian mechanics for further details.

[edit] Existence and uniqueness

The local existence and uniqueness theorem for geodesics states that geodesics on a smooth manifold with an affine connection exist, and are unique; this is a variant of the Frobenius theorem. More precisely:

For any point p in M and for any vector V in TpM (the tangent space to M at p) there exists a unique geodesic 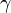\gamma \, : I → M such that
\gamma(0) = p \, and
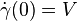\dot\gamma(0) = V,
where I is a maximal open interval in R containing 0.

In general, I may not be all of R as for example for an open disc in R2. The proof of this theorem follows from the theory of ordinary differential equations, by noticing that the geodesic equation is a second-order ODE. Existence and uniqueness then follow from the Picard-Lindelöf theorem for the solutions of ODEs with prescribed initial conditions. γ depends smoothly on both p and V.

[edit] Geodesic flow

Geodesic flow is an \mathbb R-action on tangent bundle T(M) of a manifold M defined in the following way

G^t(V)=\dot\gamma_V(t)

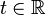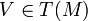where t\in \mathbb R, V\in T(M) and γV denotes the geodesic with initial data \dot\gamma_V(0)=V.

It defines a Hamiltonian flow on (co)tangent bundle with the (pseudo-)Riemannian metric as the Hamiltonian. In particular it preserves the (pseudo-)Riemannian metric g, i.e.

g(Gt(V),Gt(V)) = g(V,V).

That makes possible to define geodesic flow on unit tangent bundle UT(M) of the Riemannian manifold M when the geodesic γV is of unit speed.

A closed orbit of the geodesic flow corresponds to a closed geodesic on M.

[edit] Geodesic spray

The geodesic flow defines a family of curves in the tangent bundle. The derivatives of these curves define a vector field on the total space of the tangent bundle, known as the geodesic spray.

[edit] Affine and projective geodesics

In the presence of a metric, geodesics are (locally) the length-minimizing curves. However, even if a manifold lacks a metric, geodesics are still well-defined in the presence of an affine connection. A curve in such a manifold is a geodesic if its tangent vector remains parallel to the curve when it is transported along it. Geodesics defined in this way carry a preferred class of affine parametrizations. These are those parametrizations for which

\nabla_{\dot{\gamma}(t)}\dot{\gamma}(t) = 0.

This equation is invariant under affine reparametrizations; that is, parametrizations of the form

t\mapsto at+b

where a and b are constant real numbers.

An affine connection is determined by its family of affinely parameterized geodesics, up to torsion (Spivak 1999, Chapter 6, Addendum I). The torsion itself does not, in fact, affect the family of geodesics, since the geodesic equation depends only on the symmetric part of the connection. More precisely, if 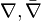\nabla, \bar{\nabla} are two connections such that the difference tensor

D(X,Y) = \nabla_XY-\bar{\nabla}_XY

is skew-symmetric, then \nabla and \bar{\nabla} have the same geodesics, with the same affine parameterizations. Furthermore, there is a unique connection having the same geodesics as \nabla, but with vanishing torsion.

Geodesics without a particular parameterization are described by a projective connection.

[edit] See also

[edit] References

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Geodesic"
Personal tools