Rational trigonometry
From Wikipedia, the free encyclopedia
| This article relies largely or entirely upon a single source. Please help improve this article by introducing appropriate citations of additional sources. (January 2009) |
Divine Proportions: Rational Trigonometry to Universal Geometry is a book by Norman J. Wildberger, an outspoken critic of traditional mathematics, presenting his reformulation of trigonometry. Wildberger holds a Ph.D. in mathematics from Yale University, and taught at Stanford University from 1984 to 1986 and at the University of Toronto from 1986 to 1989; he is currently an associate professor of mathematics at the University of New South Wales, Australia.
Contents |
[edit] Quadrance and spread
Instead of distance and angle, rational trigonometry uses as its fundamental units quadrance (square of distance) and spread (square of sine of angle).[1] This choice of variables enables calculations to produce output results whose complexity matches that of the input data. For instance, in a typical trigonometry problem if rational numbers are assigned to all quadrances and spreads, then the calculated results will be rational numbers (or roots of rational numbers).
This rationality is obtained at the expense of linearity. Unlike the traditional distance and angle units, doubling or halving a quadrance or spread does not double or halve a length or a rotation. Similarly, the sum of two lengths or rotations is not the sum of their individual quadrances or spreads.
For distinction, Wildberger refers to the traditional trigonometry as classical trigonometry. It is otherwise broadly based on Cartesian analytic geometry, with a point defined as an ordered pair (x, y) and a line as a general linear equation
The mathematics of rational trigonometry is, applications aside, a special instance of the description of geometry in terms of linear algebra (using rational methods such as dot products and quadratic forms), but students who are first learning trigonometry are often not taught about the use of linear algebra in geometry. Changing this state of affairs is a stated aim of Wildberger's book (to paraphrase his comments).
[edit] Trigonometry over finite fields
Rational trigonometry makes it possible to do trigonometry over finite fields in the same way as over the field of real numbers.
[edit] Quadrance
The quadrance is the square of the distance.[1]
Quadrance and distance are concerned with the separation of points. Quadrance differs from standard distance in that it squares the distance. Most immediately, this means that calculating the distance (or, more accurately, quadrance) between two points in 2-dimensional space is easier, as there is no need to find the square root of the sum of the squares of the differences in the x and y coordinates.
In the (x, y)-plane, the quadrance Q(A1, A2) for the points A1 and A1 is defined as
[edit] Spread
Spread, a measure of the separation of lines, is a dimensionless number in the range [0, 1]. The value of the spread is the square of the sine of the angle.[1]
Suppose two lines, ℓ 1 and ℓ 2, intersect at the point A as shown at right. Choose a point B ≠ A on ℓ 1 and let C be the foot of the perpendicular from B to ℓ 2. Then the spread s is
See also spread polynomials.
[edit] Spread compared to angle
In rational trigonometry, spread is a fundamental concept, somewhat but not precisely corresponding to the concept in traditional geometry of angle. Spread describes a relationship between two lines, whereas angle describes a relationship between two rays emanating from a common point.[1]
The spread is the square of the sine of the angle.
| Degree | Radian | Spread |
|---|---|---|
| 0 | 0 | 0 |
| 30 | (1/6)π | 1/4 |
| 45 | (1/4)π | 1/2 |
| 60 | (1/3)π | 3/4 |
| 90 | (1/2)π | 1 |
| 120 | (2/3)π | 3/4 |
| 135 | (3/4)π | 1/2 |
| 150 | (5/6)π | 1/4 |
| 180 | π | 0 |
Spread is not proportional to degrees or radians, and has a period of 180 degrees (π radians).
[edit] Laws of rational trigonometry
Wildberger states that there are five basic laws in rational trigonometry and these laws can be easily verified using high-school level mathematics. Some are equivalent to standard trigonometrical formulae with the variables expressed as quadrance and spread.[1]
[edit] Triple quad formula
The three points A1,A2,A3 are collinear precisely when:
This is equivalent to using Heron's formula, the condition for collinearity being that the triangle formed by the three points has zero area.
It can either be proved by analytic geometry (the preferred means within rational trigonometry) or derived from Heron's formula, using the condition for collinearity that the triangle formed by the three points has zero area.
The line  has the general form:
has the general form:
where the (non-unique) parameters  ,
, 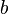 and
and  , can be expressed in terms of the coordinates of points
, can be expressed in terms of the coordinates of points 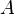 and
and 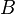 as:
as:
so that, everywhere on the line:
But the line can also be specified by two simultaneous equations in a parameter 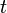 , where
, where  at point
at point 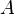 and
and  at point
at point 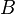 :
:
 and
and 
or, in terms of the original parameters:
 and
and 
If the point  is collinear with points
is collinear with points 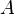 and
and 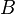 , there exists some value of
, there exists some value of 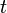 (for distinct points, not equal to 0 or 1), call it
(for distinct points, not equal to 0 or 1), call it 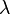 , for which these two equations are simultaneously satisfied at the coordinates of the point
, for which these two equations are simultaneously satisfied at the coordinates of the point  , such that:
, such that:
 and
and 
Now, the quadrances of the three line segments are given by the squared differences of their coordinates, which can be expressed in terms of 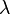 :
:
where use was made of the fact that  .
.
Substituting these quadrances into the equation to be proved:
Now, if 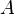 and
and 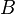 represent distinct points, such that
represent distinct points, such that  is not zero, we may divide both sides by
is not zero, we may divide both sides by  :
:
[edit] Pythagoras' theorem
The lines A1A3 and A2A3 are perpendicular precisely when:
This is equivalent to the Pythagorean theorem.
There are many classical proofs of Pythagoras' theorem; this one is framed in the terms of rational trigonometry.
The spread of an angle is the square of its sine. Given the triangle ABC with a spread of 1 between sides AB and AC,
where Q is the "quadrance", i.e. the square of the distance.
Construct a line AD dividing the spread of 1, with the point D on line BC, and making a spread of 1 with DB and DC. The triangles ABC, DBA and DAC are similar (have the same spreads but not the same quadrances).
This leads to two equations in ratios, based on the spreads of the sides of the triangle:
Now in general, the two spreads resulting from dividing a spread into two parts, as line AD does for spread CAB, do not add up to the original spread since spread is a non-linear function. So we first prove that dividing a spread of 1, results in two spreads that do add up to the original spread of 1.
For convenience, but with no loss of generality, we orient the lines intersecting with a spread of 1 to the coordinate axes, and label the dividing line with coordinates (x1,y1) and (x2,y2). Then the two spreads are given by:
Hence:
So that:
Using the first two ratios from the first set of equations, this can be rewritten:
Multiplying both sides by Q(BC):
[edit] Spread law
For any triangle  with non zero quadrances:
with non zero quadrances:
This is equivalent to the law of sines.
[edit] Cross law
For any triangle  define the cross c3 as c3 = 1 − s3. Then:
define the cross c3 as c3 = 1 − s3. Then:
This is equivalent to the law of cosines.
[edit] Triple spread formula
For any triangle 
This corresponds (roughly) to the angle sum formulae for sine and cosine.
[edit] Calculating quadrance and spread
Given the coordinates of two points (x1, y1) and (x2, y2), the quadrance between them is
Given two line segments A1A3 and A1A3 (forming an angle at point A3, the spread between them is
where Q1 is the quadrance of the side opposite the vertex A1, Q2 is the quadrance of the side opposite the vertex A2, Q3 is the quadrance of the side opposite the vertex A3.
Given the coordinates of two points on each of two lines (x11,y11), (x12,y12) and (x21,y21) (x22,y22), the spread s between them can be calculated as:
or
If the lines described by the points emanate from or are shifted to the origin by subtracting the coordinates of the first point from each line, as illustrated on the right, the computation simplifies to
[edit] See also
[edit] References
- ^ a b c d e f g Wildberger, Norman J. (2007), "A Rational Approach to Trigonometry", Math Horizons (Washington, DC: Mathematical Association of America) November 2007: 16–20, ISSN 1072-4117
- Wildberger's rational trigonometry site, including downloadable papers and sections of his book
- A comparison of classical and rational trigonometry
- Alexander Bogomolny (2007). "A brief introduction to Rational Trigonometry". Cut-the-knot. http://www.cut-the-knot.org/pythagoras/RationalTrig/CutTheKnot.shtml.







































![\begin{align}
s & = 1 - \frac{(Q_1 + Q_2 - Q_3 )^2}{4Q_1 Q_2} \\[6pt]
& = \frac{ 2Q_1 Q_2 + 2Q_1 Q_3 + 2Q_2 Q_3 - Q_1^2 - Q_2^2 - Q_3^2}{4Q_1 Q_2}
\end{align}](http://upload.wikimedia.org/math/b/5/c/b5c497db2d7b424fda33d3acefffdaba.png)




