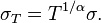Volatility (finance)

From Wikipedia, the free encyclopedia

Jump to: navigation, search
 This article does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (February 2009)

Volatility most frequently refers to the standard deviation of the continuously compounded returns of a financial instrument with a specific time horizon. It is often used to quantify the risk of the instrument over that time period. Volatility is typically expressed in annualized terms, and it may either be an absolute number ($5) or a fraction of the mean (5%). Volatility can be traded directly in today's markets through options and variance swaps.

For a financial instrument whose price follows a Gaussian random walk, or Wiener process, the volatility increases as time increases. Conceptually, this is because there is an increasing probability that the instrument's price will be farther away from the initial price as time increases. However, rather than increase linearly, the volatility increases with the square-root of time as time increases, because some fluctuations are expected to cancel each other out, so the most likely deviation after twice the time will not be twice the distance from zero.

More broadly, volatility refers to the degree of (typically short-term) unpredictable change over time of a certain variable. It may be measured via the standard deviation of a sample, as mentioned above. However, price changes actually do not follow Gaussian distributions. Better distributions used to describe them actually have "fat tails" although their variance remains finite. Therefore, other metrics may be used to describe the degree of spread of the variable. As such, volatility reflects the degree of risk faced by someone with exposure to that variable.

Historical volatility (or ex-post volatility) is the volatility of a financial instrument based on historical returns. This phrase is used particularly when it is wished to distinguish between the actual volatility of an instrument in the past, and the current (ex-ante, or forward-looking) volatility implied by the market.

Contents

[edit] Volatility for market players

Volatility is often viewed as a negative in that it represents uncertainty and risk. However, volatility can be good in that if one shorts on the peaks, and buys on the lows one can make money, with greater money coming with greater volatility. The possibility for money to be made via volatile markets is how short term market players like day traders hope to make money, and is in contrast to the long term investment view of buy and hold.

In today's markets, it is also possible to trade volatility directly, through the use of derivative securities such as options and variance swaps. See Volatility arbitrage.

[edit] Volatility versus direction

Volatility does not imply direction. (This is due to the fact that all changes are squared.) An instrument that is more volatile is likely to increase or decrease in value more than one that is less volatile.

For example, a savings account has low volatility. While it won't lose 50% in a year, it also won't gain 50%.

[edit] Volatility over time

It's common knowledge that types of assets experience periods of high and low volatility. That is, during some periods prices go up and down quickly, while during other times they might not seem to move at all.

Periods when prices fall quickly (a crash) are often followed by prices going down even more, or going up by an unusual amount. Also, a time when prices rise quickly (a bubble) may often be followed by prices going up even more, or going down by an unusual amount.

The converse behavior, 'doldrums' can last for a long time as well.

Most typically, extreme movements do not appear 'out of nowhere'; they're presaged by larger movements than usual. This is termed autoregressive conditional heteroskedasticity. Of course, whether such large movements have the same direction, or the opposite, is more difficult to say. And an increase in volatility does not always presage a further increase—the volatility may simply go back down again.

Over time volatility always increases.

[edit] Mathematical definition

The annualized volatility σ is the standard deviation σ of the instrument's logarithmic returns in a year.

The generalized volatility σT for time horizon T in years is expressed as:

\sigma_T = \sigma \sqrt{T}.\,

For example, if the daily logarithmic returns of a stock SigmaSD have a standard deviation of 0.01 and there are 252 trading days in a year, then the time period of returns P is 1/252 and annualized volatility is

\sigma = {\sigma_{SD}\over\sqrt{P}},\,
\sigma = {0.01 \over \sqrt{\frac{1}{252}}} = 0.1587.

The monthly volatility (i.e., T = 1 / 12 of a year) would be

\sigma_\text{month} = 0.1587 \sqrt{\frac{1}{12}} = 0.0458.

Note that the formula used to annualize returns is not deterministic, but is an extrapolation valid for a random walk process whose steps have finite variance. Generally, the relation between volatility in different time scales is more complicated, involving the Lévy stability exponent α:

\sigma_T = T^{1/\alpha} \sigma.\,

If α = 2 you get the Wiener process scaling relation, but some people believe α < 2 for financial activities such as stocks, indexes and so on. This was discovered by Benoît Mandelbrot, who looked at cotton prices and found that they followed a Lévy alpha-stable distribution with α = 1.7. (See New Scientist, 19 April, 1997].) Mandelbrot's conclusion is, however, not accepted by mainstream financial econometricians.

[edit] Quick-and-dirty (percentage) volatility measurement

Suppose you notice that a market price index which is approximately 10,000, moves about 100 points a day on average. This would constitute a 1% (up or down) daily movement. To annualize this, you can use the "rule of 16", that is, multiply by 16 to get 16% as the overall (annual) volatility. The rationale for this is that 16 is the square root of 256, which is approximately the number of actual trading days in a year. This uses the statistical result that the standard deviation of the sum of n independent variables (with equal standard deviations) is 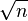\sqrt{n} times the standard deviation of the individual variables. It also takes the average magnitude of the observations as an approximation to the standard deviation of the variables. Under the assumption that the variables are normally distributed with mean zero and standard deviation σ, the expected value of the magnitude of the observations is \sqrt{2 \over \pi}\sigma = 0.798\sigma, thus the observed average magnitude of the observations may be taken as a rough approximation to σ.

[edit] See also

[edit] References

 This article does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (June 2008)

[edit] External links

v • d • e
Volatility
Modelling volatility
Trading volatility
Retrieved from "http://en.wikipedia.org/wiki/Volatility_(finance)"
Personal tools