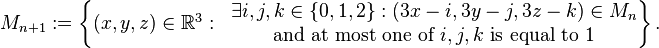%5Bwikipedia_article%5D 3d cantor-set ciencia cube curve design eduardo.ortiz.blog fractal fractals geometry inspiration inspritation interesting math mathematics menger menger-sponge menger_sponge nerd pajero puzzles quizzlematerial science sculpture sierpinski-carpet visualization

My tags:

From Wikipedia, the free encyclopedia

In mathematics, the Menger sponge is a fractal curve. It is the universal curve, in that it has topological dimension one, and any other curve (more precisely: any compact metric space of topological dimension 1) is homeomorphic to some subset of it. It is sometimes called the Menger-Sierpinski sponge or the Sierpinski sponge. It is a three-dimensional extension of the Cantor set and Sierpinski carpet. It was first described by Austrian mathematician Karl Menger in 1926 while exploring the concept of topological dimension.

Contents 1 Construction 2 Properties 3 Formal definition 4 In film 5 See also 6 References 7 External links

[edit] Construction

Construction of a Menger sponge can be visualized as follows:

1. Begin with a cube. (first image)
2. Divide every face of the cube into 9 squares. This will sub-divide the cube into 27 smaller cubes, like a Rubik's Cube
3. Remove the cube at the middle of every face, and remove the cube in the center, leaving 20 cubes (second image). This is a Level 1 Menger sponge.
4. Repeat steps 1-3 for each of the remaining smaller cubes.

The second repetition will give you a Level 2 sponge (third image), the third a Level 3 sponge (fourth image), and so on. The Menger sponge itself is the limit of this process after an infinite number of iterations.

The number of cubes is 20ⁿ, with n being the number of iterations performed on the first cube:

Iters	Cubes
0	1
1	20
2	400
3	8,000
4	160,000
5	3,200,000
6	64,000,000

At the first level, no iterations are performed, (20⁰ = 1).

[edit] Properties

Each face of the Menger sponge is a Sierpinski carpet; furthermore, any intersection of the Menger sponge with a diagonal or medium of the initial cube M₀ is a Cantor set.

The Menger sponge is a closed set; since it is also bounded, the Heine-Borel theorem implies that it is compact. Furthermore, the Menger sponge is uncountable and has Lebesgue measure 0.

The topological dimension of the Menger sponge is one, the same as any curve. Menger showed, in the 1926 construction, that the sponge is a universal curve, in that any possible one-dimensional curve is homeomorphic to a subset of the Menger sponge, where here a curve means any compact metric space of Lebesgue covering dimension one; this includes trees and graphs with an arbitrary countable number of edges, vertices and closed loops, connected in arbitrary ways.

In a similar way, the Sierpinski carpet is a universal curve for all curves that can be drawn on the two-dimensional plane. The Menger sponge constructed in three dimensions extends this idea to graphs that are not planar, and might be embedded in any number of dimensions. Thus any geometry of quantum loop gravity can be embedded in a Menger sponge.

Interestingly, the Menger sponge simultaneously exhibits an infinite surface area and encloses zero volume.

The sponge has a Hausdorff dimension of (log 20) / (log 3) (approx. 2.726833).

[edit] Formal definition

Formally, a Menger sponge can be defined as follows:

where M₀ is the unit cube and

[edit] In film

A fictitious version of the Menger Sponge that appeared to have the abilities of controlling the effects of gravity on oneself and capturing ghosts (among other properties) was featured in the 2006 Taiwanese film Gui si (Silk)

[edit] See also

• List of fractals by Hausdorff dimension
• Sierpinski triangle
• Sierpinski tetrahedron
• Koch snowflake

[edit] References

• Karl Menger, General Spaces and Cartesian Spaces, (1926) Communications to the Amsterdam Academy of Sciences. English translation reprinted in Classics on Fractals, Gerald A.Edgar, editor, Addison-Wesley (1993) ISBN 0-201-58701-7
• Karl Menger, Dimensionstheorie, (1928) B.G Teubner Publishers, Leipzig.

[edit] External links

Wikimedia Commons has media related to: Menger sponge

• An interactive Menger sponge
• Fractal polyhedra (VRML) and interactive Java models
• Puzzle Hunt — Video explaining Zeno's paradoxes using Menger-Sierpinski sponge
• The Business Card Menger Sponge Project
• Menger Sponge Assembly Construction of a Level-3 Menger Sponge from business cards
• Mengermania — Construction of a Level 4 Menger Sponge from index cards with detailed status updates
• Menger Sponge Animations — Menger Sponge Animations up to Level 9, discussion of optimization for 3d.
• L3 Menger Sponge with business cards 2006 - An L3 Menger Sponge by students at Cornell College built in 2006
• Level 3 Menger Sponge made of Business Cards - A Level 3 Menger Sponge built by students at Mississippi State University out of 48,000 folded business cards.
• Menger sphere, rendered in SunFlow