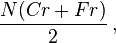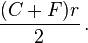Annual percentage rate

From Wikipedia, the free encyclopedia

Jump to: navigation, search
 This article may require cleanup to meet Wikipedia's quality standards. Please improve this article if you can. (January 2009)

The terms annual percentage rate (APR), nominal APR, and effective APR (EAR)[1] describe the interest rate for a whole year (annualized), rather than just a monthly fee/rate, as applied on a loan, mortgage, credit card, etc. It is a finance charge expressed as an annual rate. [2] Those terms have formal, legal definitions in some countries or legal jurisdictions, but in general: [1]

  • The nominal APR is the simple-interest rate (for a year).
  • The effective APR is the fee+compound interest rate (calculated across a year).[1]

The nominal APR is calculated as: the rate, for a payment period, multiplied by the number of payment periods in a year.[1] However, the exact legal definition of "effective APR", or EAR in short, can vary greatly in each jurisdiction, depending on the type of fees included, such as participation fees, loan origination fees, monthly service charges, or late fees. The effective APR has been called the "mathematically-true" interest rate for each year.[3][4] The computation for the effective APR, as the fee+compound interest rate, can also vary depending on whether the up-front fees, such as origination or participation fees, are added to the entire amount, or treated as a short-term loan due in the first payment. When start-up fees are paid as first payment(s), the balance due might accrue more interest, as being delayed by the extra payment period(s).[5]

In some areas, the annual percentage rate (APR) is the simplified counterpart to the effective interest rate that the borrower will pay on a loan. When not using the term "effective APR", the use of "APR" is an early term for nominal APR. In many countries and jurisdictions, lenders (such as banks) are required to disclose the "cost" of borrowing in some standardized way as a form of consumer protection. APR is intended to make it easier to compare lenders and loan options. The APR is likely to differ from the "note rate" or "headline rate" advertised by the lender, due to the addition of other fees that may need to be included in the APR. APRs can be found by asking the lender or by reading the appropriate section in the contract.

In the U.S. and the UK, lenders are required to disclose the APR before the loan (or credit application) is finalized (although the definition of "APR" is not the same in these two countries – see below). Credit card companies can advertise monthly interest rates, but they are required to clearly state the annual percentage rate before an agreement is signed. APR is a term used with regard to deposit accounts as well. However, when dealing with deposit accounts, the annual percentage yield (APY) or annual equivalent rate (AER) is quoted to consumers for comparison purposes.

Contents

[edit] Confusion of terminology

The terms APR, nominal APR, and effective APR (EAR) can seem confusing, especially due to multiple definitions of each term. An early use of the term "APR" was as only the annual simple-interest rate (without compound interest), which typically became called the "nominal APR" at a later time. The newer term "effective APR" (for fees+interest compounded) treats the meaning of "APR" as being simply an annualized rate, rather than using an earlier meaning of APR as meaning the nominal APR (simple interest for a year).[1]

To further confuse the meanings, sometimes the effective APR is considered as merely identical to compound interest, to only compounding the interest rate (for each year), without computing any extra fees into the total rate. More complex calculations, for effective APR, will amortize the origination fees as a short-term loan, due in the first payment(s), then amortize the unpaid balance as a long-term loan, delayed even longer, by the extra first payment(s) being dedicated to primarily paying origination fees, and interest charges on that portion. Other calculations for effective APR can simply add origination fees to the balance due, and then treat the total amount as the basis for computing compound interest on that larger balance due.

If the word "effective" is used, separately, as meaning "influential" (or having a "long-range effect"), then the term effective APR will vary as being an expression, rather than a strict legal definition. Plus when "APR" is treated as an abbreviation for the word "April" (4th month), then the term "effective APR" means "going into effect in April" (as a very common legal definition for the separate word "effective").

All of the above, sources of confusion, do not even consider the distinction between interest compounded for each time period, versus interest compounded daily, on any remaining balance left. Some credit cards can compound interest daily,[1] even though payments are due monthly.

Another source of confusion is the concept of having an annual (year-long) rate for a short-term loan. For example, a one-month payday loan at 5% interest for the month, has a (year-long) effective APR of over 79% (1.05^12 =~1.7958). If a payday loan were for US$100 plus 5%, but added a $10 fee also due, the interest increases by 10% ($10/$100) for the month, with the effective APR at nearly 435% (1.15^12 =~5.3502, as 535%-100%=435%). The resulting effective APR of 435% can seem very confusing, starting from a $10 fee; however, the issue is the fair value of money, when considered in relation to a full year.

[edit] Rate format

 This section does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (November 2008)

An effective annual interest rate of 10% can also be expressed in several ways:

  • 0.7974% effective monthly interest rate, because 1.007974^12=1.1
  • 9.569% annual interest rate compounded monthly, because 12*0.7974=9.569
  • 9.091% annual rate in advance, because 1/1.1=1-0.091

These rates are all equivalent, but to a consumer who is not trained in the mathematics of finance, this can be confusing. APR helps to standardize how interest rates are compared, so that a 10% loan is not made to look cheaper by calling it a loan at "9.1% annually in advance".

The APR does not necessarily convey the total amount of interest paid over the course of a year: if one pays part of the interest prior to the end of the year, the total amount of interest paid is less.

In the case of a loan with no fees, the amortization schedule would be worked out by taking the principal left at the end of each month, multiplying by the monthly rate and then subtracting the monthly payment. This can be expressed mathematically by

p = \frac{P_0*r^{(n+1)}}{\displaystyle{\sum_{l=1}^n r^l}}

where:
P0 is the initial principal
r is the percentage rate used each payment
n is the number of payments

This also explains why a 15 year mortgage and a 30 year mortgage with the same APR would have different monthly payments and a different total amount of interest paid. There are many more periods over which to spread the principal, which makes the payment smaller, but there are just as many periods over which to charge interest at the same rate, which makes the total amount of interest paid much greater. For example, $100,000 mortgaged (without fees, since they add into the calculation in a different way) over 15 years costs a total of $193,429.80 (interest is 93.430% of principal), but over 30 years, costs a total of $315,925.20 (interest is 215.925% of principal).

In addition the APR takes costs into account. Suppose for instance that $100,000 is borrowed with $1000 one-time fees paid in advance. If, in the second case, equal monthly payments are made of $946.01 against 9.569% compounded monthly then it takes 240 months to pay the loan back. If the $1000 one-time fees are taken into account then the yearly interest rate paid is effectively equal to 10.31%.

The APR concept can also be applied to savings accounts: imagine a savings account with 1% costs at each withdrawal and again 9.569% interest compounded monthly. Suppose that the complete amount including the interest is withdrawn after exactly one year. Then, taking this 1% fee into account, the savings effectively earned 8.9% interest that year.

[edit] Money factor

The APR can also be represented by a money factor (also known as the lease factor, lease rate, or factor). The money factor is usually given as a decimal, for example .0030. To find the equivalent APR, the money factor is multiplied by 2400. A money factor of .0030 is equivalent to a monthly interest rate of 0.6% and an APR of 7.2%.[6]

For a leasing arrangement with an initial capital cost of C, a residual value at the end of the lease of F and a monthly interest rate of r, monthly interest starts at Cr and decreases almost linearly during the term of the lease to a final value of Fr.[7] The total amount of interest paid over the lease term of N months is therefore

\frac{N(Cr+Fr)}{2}\, ,

and the average interest amount per month is

\frac{(C+F)r}{2}\, .

This amount is called the "monthly finance fee".[8] The factor r/2 is called the "money factor"

[edit] Failings

Despite repeated attempts by regulators to establish usable and consistent standards, APR does not represent the total cost of borrowing nor does it really create a comparable standard. Nevertheless, it is considered a reasonable starting point for an ad-hoc comparison of lenders.

[edit] Does not represent the total cost of borrowing

Credit card holders should be aware that most U.S. credit cards are quoted in terms of nominal APR compounded monthly, which is not the same as the effective annual rate (EAR). Despite the "Annual" in APR, it is not necessarily a direct reference for the interest rate paid on a stable balance over one year. The more direct reference for the one-year rate of interest is EAR. The general conversion factor for APR to EAR is EAR=((1+APR/n)^n)-1, where n represents the number of compounding periods of the APR per EAR period. E.g., for a common credit card quoted at 12.99% APR compounded monthly, the one year EAR is ((1+.129949/12)^12)-1, or 13.7975%. For 12.99% APR compounded daily, the EAR paid on a stable balance over one year becomes 13.87% (see credit card interest for the .000049 addition to the 12.99% APR). Note that a high U.S. APR of 29.99% compounded monthly carries an effective annual rate of 34.48%.

While the difference between APR and EAR may seem trivial, because of the exponential nature of interest these small differences can have a large effect over the life of a loan. For example, consider a 30-year loan of $200,000 with a stated APR of 10.00%, i.e., 10.0049% APR or the EAR equivalent of 10.4767%. The monthly payments, using APR, would be $1755.87. However, using an EAR of 10.00% the monthly payment would be $1691.78. The difference between the EAR and APR amounts to a difference of $64.09 per month. Over the life of a 30-year loan, this amounts to $23,070.86, which is over 11% of the original loan amount.

Some classes of fees are deliberately not included in the calculation of APR. Because these fees are not included, some consumer advocates claim that the APR does not represent the total cost of borrowing. Excluded fees may include:

  • routine one-time fees which are paid to someone other than the lender (such as a real estate attorney's fee)
  • penalties such as late fees or service reinstatement fees without regard for the size of the penalty or the likelihood that it will be imposed.

Lenders argue that the real estate attorney's fee, for example, is a pass-through cost, not a cost of the lending. In effect, they are arguing that the attorney's fee is a separate transaction and not a part of the loan. Consumer advocates argue that this would be true if the customer is free to select which attorney is used. If the lender insists on using a specific attorney however, then the cost should be looked at as a component of the total cost of doing business with that lender. This area is made more complicated by the practice of contingency fees – for example, when the lender receives money from the attorney and other agents to be the one used by the lender. Because of this, U.S. regulators require all lenders to produce an affiliated business disclosure form which shows the amounts paid between the lender and the appraisal firms, attorneys, etc.

Lenders argue that including late fees and other conditional charges would require them to make assumptions about the consumer's behavior — assumptions which would bias the resulting calculation and create more confusion than clarity.

[edit] Not a comparable standard

Even beyond the non-included cost components listed above, regulators have been unable to completely define which one-time fees must be included and which excluded from the calculation. This leaves the lender with some discretion to determine which fees will be included (or not) in the calculation.

Consumers can, of course, use the nominal interest rate and any costs on the loan (or savings account) and compute the APR themselves, for instance using one of the calculators on the internet.

In the example of a mortgage loan, the following kinds of fees are:

Generally included:

Sometimes included:

Generally not included:

The discretion that is illustrated in the "sometimes included" column even in the highly regulated U.S. home mortgage environment makes it difficult to simply compare the APRs of two lenders. Note: U.S. regulators generally require a lender to use the same assumptions and definitions in their calculation of APR for each of their products even though they cannot force consistency across lenders.

With respect to items that may be sold with vendor financing, for example, automobile leasing, the notional cost of the good may effectively be hidden and the APR subsequently rendered meaningless. An example is a case where an automobile is leased to a customer based on a "manufacturer's suggested retail price" with a low APR: the vendor may be accepting a lower lease rate as a trade-off against a higher sale price. Had the customer self-financed, a discounted sales price may have been accepted by the vendor; in other words, the customer has received cheap financing in exchange for paying a higher purchase price, and the quoted APR understates the true cost of the financing. In this case, the only meaningful way to establish the "true" APR would involve arranging financing through other sources, determining the lowest-acceptable cash price and comparing the financing terms (which may not be feasible in all circumstances). For leases where the lessee has a purchase option at the end of the lease term, the cost of the APR is further complicated by this option. In effect, the lease includes a put option back to the manufacturer (or, alternatively, a call option for the consumer), and the value (or cost) of this option to the consumer is not transparent.

[edit] Dependence on loan period

APR is dependent on the time period for which the loan is calculated. That is, the APR for one loan with a 30 year loan duration cannot be compared to the APR for another loan with a 20 year loan duration. APR can be used to show the relative impact of different payment schedules (such as balloon payments or bi-weekly payments instead of straight monthly payments), but most standard APR calculators have difficulty with those calculations.

Furthermore, most APR calculators assume that an individual will keep a particular loan until it is completely paid off resulting in the up-front fixed closing costs being amortized over the full term of the loan. If the consumer pays the loan off early, the effective interest rate achieved will be significantly higher than the APR initially calculated. This is especially problematic for mortgage loans where typical loan durations are 15 or 30 years but where many borrowers move or refinance before the loan period runs out.

In theory, this factor should not affect any individual consumer's ability to compare the APR of the same product (same duration loan) across vendors. APR may not, however, be particularly helpful when attempting to compare different products.

[edit] Interest-only loans

Since the principal loan balance is not paid down during the interest-only term, the total interest paid over the lifetime of the loan is increased and the APR is higher than a loan without an interest-only payment period.

Three lenders with identical information may still calculate different APRs. The calculations can be quite complex and are poorly understood even by most financial professionals. Most users depend on software packages to calculate APR and are therefore dependent on the assumptions in that particular software package. While differences between software packages will not result in large variations, there are several acceptable methods of calculating APR, each of which returns a slightly different result.

[edit] Region-specific details

[edit] United States

In the U.S., the calculation and disclosure of APR is governed by the Truth in Lending Act (also known as Regulation Z). In general, APR in the United States is expressed as the periodic interest rate times the number of compounding periods in a year[9] (also known as the nominal interest rate); since the APR must include certain non-interest charges and fees, however, it requires more detailed calculation.

The calculation for "close-ended credit" (such as a home mortgage or auto loan) can be found here. The calculation for "open-ended credit" (such as a credit card, home equity loan or other line of credit) can be found here.

[edit] European Union

In the EU, the focus of APR standardization is heavily on the standardization of the time-value of the interest calculation. As of Oct 2005, the EU still allows Member States to determine the specific cost-components to be included in the APR calculation.

A single method of calculating the APR was introduced in directive 98/7/EC and is required to be published for the major part of loans. The basic equation for calculation of APR in the EU is:

\sum_{l=1}^M S_l (1 + \mathrm{APR}/100)^{-t_l} = \sum_{k=1}^N A_k (1 + \mathrm{APR}/100)^{-t_k}
where:
M is the number of cash flows paid by the lender
l is the sequence number for the cash flows paid by the lender (draw down)
Sl is the cash flow (drawdown) in period l
N is the total number of cash flows paid by the borrower
k is the sequence number of the cash flows paid by the borrower (repayment)
Ak is the cash flow (repayment) of period k, and
tl and tk is the interval, expressed in years and fractions of a year between the date of the first cash flow and the date of cash flow l or k. (t1 = 0.)

In this equation the left side is the present value of the draw downs made by the lender and the right side is the present value of the repayments made by the borrower. In both cases the present value is defined given the APR as the interest rate. So the present value of the drawdowns is equal to the present value of the repayments, given the APR as the interest rate.

Note that neither the amounts nor the periods between transactions are necessarily equal. For the purposes of this calculation, a year is presumed to have 365 days (366 days for leap years), 52 weeks or 12 equal months. An equal month is presumed to have 30.41666 days regardless of whether or not it is a leap year. The result is to be expressed to at least one decimal place. This algorithm for APR is required for some but not all forms of consumer debt in the EU. For example, this EU directive is limited to agreements of €50,000 and below and excludes all mortgages.[1]

In the Netherlands the formula above is also used for mortgages. In many cases the mortgage is not always paid back completely at the end of period N, but for instance when the borrower sells his house or dies. In addition there is usually only one payment of the lender to the borrower: in the beginning of the loan. In that case the formula becomes:

S -A = R (1 + \mathrm{APR}/100)^{-t_N} + \sum_{k=1}^N A_k (1 + \mathrm{APR}/100)^{-t_k}
where:
S is the borrowed amount
A is the prepaid onetime fee
R the rest debt, the amount that remains as an interest-only loan after the last cash flow.

If the length of the periods are equal (monthly payments) then the summations can be simplified using the formula for a geometric series. Either way the APR can only be solved iteratively from the formulas above, apart from trivial cases such as N = 1.

[edit] UK

APR was introduced under the Consumer Credit Act 1974, to ensure comparability of loans – and is required to be published for all regulated loans. The APR must be more prominent than any other rate or charge.

The method used to calculate APRs in the EU and UK is different from that used in the U.S. and will often produce different (higher) results. This is because the U.S. method (regulation "Z") produces what would, in the UK, be called a nominal annual rate whereas the UK/EU method results in an effective annual rate.

[edit] See also

[edit] References

  1. ^ a b c d e f "Subject: Regulation AA", Alfred F. "Bob" Blair, Jr., US Federal Reserve, 2008-06-28, webpage: US-Federal-Reserve-R1314.
  2. ^ Sullivan, arthur; Steven M. Sheffrin (2003). Economics: Principles in action. Upper Saddle River, New Jersey 07458: Pearson Prentice Hall. pp. 514. ISBN 0-13-063085-3. http://www.pearsonschool.com/index.cfm?locator=PSZ3R9&PMDbSiteId=2781&PMDbSolutionId=6724&PMDbCategoryId=&PMDbProgramId=12881&level=4. 
  3. ^ "The Financial Literacy Crisis", April 2008, US News and World Report, webpage: USNews-Your-Money-101.
  4. ^ "President's Advisory Council on Financial Literacy", January 2008, Rossputin.com, webpage: [http:www.rossputin.com/blog/index.php/2008/01/24/president_s_advisory_council_on_financia Rossputin-FinLiteracy].
  5. ^ "Margill - Loans, Lines of credit, APR" (calculation types), Margill/Jurismedia inc., 2008, webpage: Margill-en.
  6. ^ Reed, Philip. "Leasing Glossary". http://www.edmunds.com/advice/leasing/articles/47281/article.html. Retrieved on 2008-03-18. 
  7. ^ Money Factor Definition, efunda Engineering Fundamentals
  8. ^ Monthly Lease Payments, leaseguide.com
  9. ^ http://www.uncdf.org/mfdl/readings/EIR_Tucker.pdf Tucker, William R. "Effective Interest Rate," Paper, Bankakademie Micro Banking Competence Center, 5-6 September 2000.

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Annual_percentage_rate"
Personal tools