#238 academic algorithm algorithms article_math bbs blum-blum-shub challenge cipher computer-science crypto cryptography cränk cs cthulhu drm encryption felipe generator math mathematics numerics programming projecteuler pseudo-random random randomness rng security

My tags:

From Wikipedia, the free encyclopedia

Blum Blum Shub (B.B.S.) is a pseudorandom number generator proposed in 1986 by Lenore Blum, Manuel Blum and Michael Shub (Blum et al, 1986).

Blum Blum Shub takes the form:

x_n+1 = (x_n)² mod M

where M=pq is the product of two large primes p and q. At each step of the algorithm, some output is derived from x_n; the output is commonly either the bit parity of x_n or one or more of the least significant bits of x_n.

The two primes, p and q, should both be congruent to 3 (mod 4) (this guarantees that each quadratic residue has one square root which is also a quadratic residue) and gcd(φ(p-1), φ(q-1)) should be small (this makes the cycle length large).

An interesting characteristic of the Blum Blum Shub generator is the possibility to calculate any x_i value directly (via Euler's Theorem):

Contents 1 Security 2 Example 3 References 4 External links

[edit] Security

The generator is not appropriate for use in simulations, only for cryptography, because it is very slow. However, it has an unusually strong security proof, which relates the quality of the generator to the computational difficulty of integer factorization. When the primes are chosen appropriately, and O(log log M) lower-order bits of each x_n are output, then in the limit as M grows large, distinguishing the output bits from random will be at least as difficult as factoring M.

If integer factorization is difficult (as is suspected) then B.B.S. with large M will have an output free from any nonrandom patterns that can be discovered with any reasonable amount of calculation. This makes it as secure as other encryption technologies tied to the factorization problem, such as RSA encryption.

[edit] Example

Let p = 11, q = 19 and s = 3. We can expect to get a large cycle length for those small numbers, because gcd(φ(p − 1),φ(q − 1)) = 2. The generator starts to evaluate x₀ by using x _{− 1} = s and creates the sequence x₀, x₁, x₂, 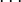x₅ = 9, 81, 82, 36, 42, 92. The following table shows different output bits of different bit is used to determine the output.

Even parity bit	Odd parity bit	Least significant bit
0 1 1 0 1 0	1 0 0 1 0 1	1 1 0 0 0 0

[edit] References

• Lenore Blum, Manuel Blum, and Michael Shub. "A Simple Unpredictable Pseudo-Random Number Generator", SIAM Journal on Computing, volume 15, pages 364–383, May 1986.
• Lenore Blum, Manuel Blum, and Michael Shub. "Comparison of two pseudo-random number generators", Advances in Cryptology: Proceedings of Crypto '82. Available as PDF.
• Martin Geisler, Mikkel Krøigård, and Andreas Danielsen. "About Random Bits", December 2004. Available as PDF and Gzipped Postscript.

[edit] External links

• GMPBBS - a GMP-based implementation of Blum Blum Shub.
• An implementation in Java (Note: this is not a correct implementation because it does not enforce p and q as being prime; it just enforces p congruent to 3 (mod 4).)
• Randomness tests