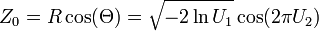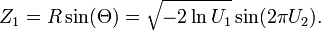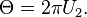Box–Muller transform

From Wikipedia, the free encyclopedia

Diagram of the Box Muller transform. The initial circles, uniformly spaced about the origin, are mapped to another set of circles about the origin that are closely spaced near the origin but quickly spread out. The largest circles in the domain map to the smallest circles in the range and vice versa.

A Box–Muller transform (by George Edward Pelham Box and Mervin Edgar Muller 1958)^[1] is a method of generating pairs of independent standard normally distributed (zero expectation, unit variance) random numbers, given a source of uniformly distributed random numbers.

It is commonly expressed in two forms. The basic form as given by Box and Muller takes two samples from the uniform distribution on the interval (0, 1] and maps them to two normally distributed samples. The polar form takes two samples from a different interval, [−1, +1], and maps them to two normally distributed samples without the use of sine or cosine functions.

One could use the inverse transform sampling method to generate normally-distributed random numbers instead; the Box–Muller transform was developed to be more computationally efficient.^[2] The more efficient Ziggurat algorithm can also be used.

[edit] Basic form

Suppose U₁ and U₂ are independent random variables that are uniformly distributed in the interval (0, 1]. Let

$Z_0 = R \cos(\Theta) =\sqrt{-2 \ln U_1} \cos(2 \pi U_2)\,$

and

$Z_1 = R \sin(\Theta) = \sqrt{-2 \ln U_1} \sin(2 \pi U_2).\,$

Then Z₀ and Z₁ are independent random variables with a normal distribution of standard deviation 1.

The derivation^[3] is based on the fact that, in a two-dimensional cartesian system where X and Y coordinates are described by two independent and normally distributed random variables, the random variables for R² and Θ (shown above) in the corresponding polar coordinates are also independent and can be expressed as

$R^2 = -2\cdot\ln U_1\,$

and

$\Theta = 2\pi U_2.\,$

[edit] Polar form

Two uniformly distributed values, u and v are used to produce the value s = R², which is likewise uniformly distributed. The definitions of the sine and cosine are then applied to the basic form of the Box–Muller transform in order to avoid using trigonometric functions.

The polar form is attributed by Devroye^[4] to Marsaglia. It is also mentioned without attribution in Carter.^[5]

Given u and v, independent and uniformly distributed in the closed interval [−1, +1], set s = R² = u² + v². (Clearly $\scriptstyle R = \sqrt{s}$ .) If s = 0 or s > 1, throw u and v away and try another pair (u, v). Continue until a pair with s in the open interval (0, 1) is found. Because u and v are uniformly distributed and because only points within the unit circle have been admitted, the values of s will be uniformly distributed in the open interval (0, 1), too. The latter can be seen by calculating the cumulative distribution function for s in the interval (0, 1). This is the area of a circle with radius $\scriptstyle \sqrt{s}$ divided by $\scriptstyle\pi$ . From this we find the probability density function to have the constant value 1 on the interval (0, 1). 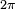Equally so, the angle θ divided by $\scriptstyle 2 \pi$ is uniformly distributed in the open interval (0, 1) and independent of s.

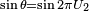We now identify the value of s with that of U₁ and $\scriptstyle \theta/(2 \pi)$ with that of U₂ in the basic form. As shown in the figure, the values of $\scriptstyle \cos \theta = \cos 2 \pi U_2$ and $\scriptstyle \sin \theta = \sin 2 \pi U_2$ in the basic form can be replaced with the ratios $\scriptstyle\cos \theta = u/R = u/\sqrt{s}$ and $\scriptstyle\sin \theta = v/R = v/\sqrt{s}$ , respectively. The advantage is that calculating the trigonometric functions directly can be avoided. This is helpful when they are comparatively more expensive than the single division that replaces each one.

Just as the basic form produces two standard normal deviates, so does this alternate calculation.

$z_0 = \sqrt{-2 \ln U_1} \cos(2 \pi U_2) = \sqrt{-2 \ln s} \left(\frac{u}{\sqrt{s}}\right) = u \cdot \sqrt{\frac{-2 \ln s}{s}}$

and

$z_1 = \sqrt{-2 \ln U_1} \sin(2 \pi U_2) = \sqrt{-2 \ln s}\left( \frac{v}{\sqrt{s}}\right) = v \cdot \sqrt{\frac{-2 \ln s}{s}}.$

[edit] Contrasting the two forms

The polar method differs from the basic method in that it is a type of rejection sampling. It throws away some generated random numbers, but it is typically faster than the basic method because it is simpler to compute (provided that the random number generator is relatively fast) and is more numerically robust.^[5] It avoids the use of trigonometric functions, which are comparatively expensive in many computing environments. It throws away 1 − π/4 ≈ 21.46% of the total input uniformly distributed random number pairs generated, i.e. throws away 4/π − 1 ≈ 27.32% uniformly distributed random number pairs per Gaussian random number pair generated, requiring 4/π ≈ 1.2732 input random numbers per output random number.

The basic form requires three multiplications, one logarithm, one square root, and one trigonometric function for each normal variate.^[6]

The polar form requires two multiplications, one logarithm, one square root, and one division for each normal variate. The effect is to replace one multiplication and one trigonometric function with a single division.

[edit] See also

Normal distribution
Inverse transform sampling
Marsaglia polar method, an optimization of the Box–Muller transform
Ziggurat algorithm, a very different way to generate normal random numbers

[edit] References

^ G. E. P. Box and Mervin E. Muller, A Note on the Generation of Random Normal Deviates, The Annals of Mathematical Statistics (1958), Vol. 29, No. 2 pp. 610-611
^ Kloeden and Platen, Numerical Solutions of Stochastic Differential Equations, pp. 11–12
^ Sheldon Ross, A First Course in Probability, (2002), pp. 279–81
^ L. Devroye: 'Non-Uniform Random Variate Generation', Springer-Verlag, New York, 1986.
^ ^a ^b Everett F. Carter, Jr., The Generation and Application of Random Numbers, Forth Dimensions (1994), Vol. 16, No. 1 & 2.
^ Note that the evaluation of $2π U 1$ is counted as a single multiplication because the value of $2π$ can be computed in advance and used repeatedly.

[edit] External links

[0] G. E. P. Box and Mervin E. Muller, A Note on the Generation of Random Normal Deviates, The Annals of Mathematical Statistics (1958), Vol. 29, No. 2 pp. 610-611

[1] Kloeden and Platen, Numerical Solutions of Stochastic Differential Equations, pp. 11–12

[2] Sheldon Ross, A First Course in Probability, (2002), pp. 279–81

[3] L. Devroye: 'Non-Uniform Random Variate Generation', Springer-Verlag, New York, 1986.

[Carter-4] Everett F. Carter, Jr., The Generation and Application of Random Numbers, Forth Dimensions (1994), Vol. 16, No. 1 & 2.

[5] Note that the evaluation of $2π U 1$ is counted as a single multiplication because the value of $2π$ can be computed in advance and used repeatedly.

[1]

[2]

[3]

[4]

[5]

[6]

Box–Muller transform

From Wikipedia, the free encyclopedia

Contents

[edit] Basic form

[edit] Polar form

[edit] Contrasting the two forms

[edit] See also

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages