Greeks (finance)

From Wikipedia, the free encyclopedia

"The Greeks" redirects here. For the ethnic group, see Greeks.

In mathematical finance, the Greeks are the quantities representing the sensitivities of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are often denoted by Greek letters. Collectively these have also been called the risk sensitivities^[1], risk measures^[2] or hedge parameters^[3].

[edit] Use of the Greeks

	Spot Price (S)	Volatility ( $σ$ )	Time to Expiry ( $τ$ )	Risk-Free Rate ( $ρ$ )
Value (V)	$Δ$ Delta	$ν$ Vega	$Θ$ Theta	$ρ$ Rho

Delta ( $Δ$ )	$Γ$ Gamma	Vanna	Charm
Gamma ( $Γ$ )	Speed	Zomma	Color

Vega ( $ν$ )	Vanna	Vomma	DvegaDtime
Vomma		Ultima

The table shows the relationship of the more common sensitivities to the four primary inputs into the Black-Scholes model (spot price of the underlying security, time remaining until option expiration, volatility and the rate of return of a risk-free investment) and to the option's value, delta, gamma, vega and vomma. Greeks which are a first-order derivative are in blue, second-order derivatives are in green and third-order derivatives are in yellow. Note that vanna is used, intentionally, in two places as these two sensitivities are mathematically equivalent.

The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging.

The Greeks in the Black-Scholes model are relatively easy to calculate, a desirable property of financial models, and are very useful for derivatives traders, especially those who seek to hedge their portfolios from adverse changes in market conditions. For this reason, those Greeks which are particularly useful for hedging delta, gamma and vega are well-defined for measuring changes in Price, Time and Volatility. Although rho is a primary input into the Black-Scholes model, the overall impact on the value of an option corresponding to changes in the risk-free interest rate is generally insignificant and therefore higher-order derivatives involving the risk-free interest rate are not common.

The most common of the Greeks are the first order derivatives: Delta, Theta, Vega and Rho as well as Gamma, a second-order derivative of the value function. The remaining sensitivities in this list are common enough that they have common names, but this list is by no means exhaustive.

[edit] Charm

$Charm = \frac{\partial \Delta}{\partial \tau} = \frac{\partial^2 V}{\partial S \partial \tau}$

Charm or delta decay, measures the instantaneous rate of change of delta over the passage of time. Charm has also been called DdeltaDtime^[4]. Charm can be an important greek to measure/monitor when delta-hedging a position over a weekend. Charm is a second order derivative of the option value, once to price and once to time.

[edit] Practical use

The mathematical result of the formula for charm (see below) is expressed in delta/year. It is often useful to divide this by the number of days per year to arrive at the delta decay per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, charm itself may change quickly, rendering full day estimates of delta decay inaccurate.

[edit] Color

$Color = \frac{\partial \Gamma}{\partial \tau} = \frac{\partial^3 V}{\partial S^2 \partial \tau}$

Color^[5], gamma decay or DgammaDtime^[6] measures the rate of change of gamma over the passage of time. Color is a third-order derivative of the option value, twice to underlying asset price and once to time. Color can be an important sensitivity to monitor when maintaining a gamma-hedged portfolio as it can help the trader to anticipate the effectiveness of the hedge as time passes.

[edit] Practical use

The mathematical result of the formula for color (see below) is expressed in gamma/year. It is often useful to divide this by the number of days per year to arrive at the change in gamma per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, color itself may change quickly, rendering full day estimates of gamma change inaccurate.

[edit] Delta

$\Delta = \frac{\partial V}{\partial S}$

Delta $Δ$ measures the rate of change of option value with respect to changes in the underlying asset's price. Delta is the first derivative of the value, $V$ , of a portfolio of derivative securities on a single underlying instrument, $S$ , with respect to the underlying instrument's price.

[edit] Practical use

Even though delta will be a number between 0.0 and 1.0 for a call and 0.0 and -1.0 for a put, these number are commonly presented as a percentage of the total number of shares represented by the option contract(s). This is convenient because the option will (instantaneously) behave like number of shares indicated by the delta. For example, if a American call option on XYZ has a delta of 0.25, it will gain or lose value just like 25% of 100 shares or 25 shares of XYZ as the price changes for small price movements.

Delta is always positive for long calls and short puts and negative for long puts and short calls. The total delta of a complex portfolio of positions on the same underlying asset can be calculated by simply taking the sum of the deltas for each individual position. Since the delta of underlying asset is always 1.0, the trader could delta-hedge his entire position in the underlying by buying or shorting the number of shares indicated by the total delta. For example, if a portfolio of options in XYZ (expressed as shares of the underlying) is +275, the trader would be able to delta-hedge the portfolio by selling short 275 shares of the underlying. This portfolio will then retain its total value regardless of which direction the price of XYZ moves. (Albeit for only small movements of the underlying, a short amount of time and not-withstanding changes in other market conditions such as volatility and the rate of return for a risk-free investment).

[edit] As a proxy for probability

Some option traders also use the absolute value of delta as an approximation of the probability that the option will expire in-the-money. For example, if an out-of-the-money call option has a delta of 0.15, the trader might estimate that the option has appropriately a 15% chance of expiring in-the-money. Similarly, if a put contract has a delta of -0.25, the trader might estimate that the likelihood of the put expiring in-the-money is 25%. (Exactly) at-the-money puts and calls have a delta of 0.5 and -0.5 respectively, or each will have an estimated 50% chance of expiring in-the-money.

[edit] Relationship between call and put delta

Given a call and put option for the same underlying, strike price and time to maturity, the sum of the absolute values of the delta of each option will be 1.00

If the value of delta for an option is known, one can compute the value of the option of the same strike price, underlying and maturity but opposite right by subtracting 1 from the known value. For example, if the delta of a call is .42 then one can compute the delta of the corresponding put a the same strike price by 0.42 - 1 = -0.58.

[edit] DvegaDtime

$\frac{\partial \nu}{\partial \tau} = \frac{\partial^2 V}{\partial \sigma \partial \tau}$

DvegaDtime^[7], measures the rate of change in the vega with respect to the passage of time. DvegaDtime is the second derivative of the value function; once to volatility and once to time.

[edit] Practical use

It is common practice to divide the mathematical result of DvegaDtime by 100 times the number of days per year to reduce the value to the percentage change in vega per one day.

[edit] Lambda

$\lambda = \frac{\partial V}{\partial S}\times\frac{1}{V}$

Lambda $λ$ , omega $Ω$ or elasticity is the percentage change in option value per change in the underlying price. It is the logarithmic derivative.

[edit] Gamma

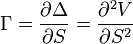$\Gamma = \frac{\partial \Delta}{\partial S} = \frac{\partial^2 V}{\partial S^2}$

Gamma $Γ$ measures the rate of change in the delta with respect to changes in the underlying price. Gamma is the second derivative of the value function with respect to the underlying price. Gamma is important because it corrects for the convexity of value.

When a trader seeks to establish an effective delta-hedge for a portfolio, the trader may also seek to neutralize the portfolio's gamma, as this will ensure that the hedge will be effective over a wider range of underlying price movements.

[edit] Rho

$\rho = \frac{\partial V}{\partial r}$

Rho $ρ$ measures sensitivity to the applicable interest rate. Rho is the derivative of the option value with respect to the risk free rate. Except under extreme circumstances, the value of an option is least sensitive to changes in the risk-free-interest rates. For this reason, rho is the least used of the primary Greeks.

[edit] Practical use

Rho is typically expressed as the amount of money, per share, that the value of the option will gain or lose as the rate of return of a risk-free investment rises or falls by 1.0%.

[edit] Speed

$Speed = \frac{\partial\Gamma}{\partial S} = \frac{\partial^3 V}{\partial S^3}$

Speed measures the rate of change in Gamma with respect to changes in the underlying price. This is also sometimes referred to as the gamma of the gamma ^[8] or DgammaDspot^[9]. Speed is the third derivative of the value function with respect to the underlying spot price. Speed can be important to monitor when delta-hedging or gamma-hedging a portfolio.

[edit] Theta

$\Theta = -\frac{\partial V}{\partial \tau}$

Theta $Θ$ , or "time decay," measures sensitivity of the value of an option to the passage of time (see Option time value).

[edit] Practical use

The mathematical result of the formula for theta (see below) is expressed in value/year. By convention, it is useful to divide the result by the number of days per year to arrive at the amount of money, per share of the underlying that the option loses in one day. Theta is always negative for long calls and puts and positive for short (or written) calls and puts. The total theta for a portfolio of options can be determined by simply taking the sum of the thetas for each individual position.

The value of an option is made up of two parts: the intrinsic value and the time value. The intrinsic value is the amount of money you would gain if you exercised the option immediately, so a call with strike $50 on a stock with price $60 would have intrinsic value of $10, whereas the corresponding put would have zero intrinsic value. The time value is the worth of having the option of waiting longer when deciding to exercise. Even a deeply out of the money put will be worth something as there is some chance the stock price will fall below the strike. However, as time approaches maturity, there is less chance of this happening, so the time value of an option is decreasing with time. Thus if you are long an option you are short theta: your portfolio will lose value with the passage of time (unless there is enough volatility to offset this).

[edit] Ultima

$Ultima = \frac{\partial vomma}{\partial \sigma} = \frac{\partial^3 V}{\partial S \partial \sigma^2}$

Ultima measures the sensitivity of the option vomma with respect to change in volatility. Ultima has also been reverred to as DvommaDvol^[10]. Ultima is a third order derivative of the option value; once to the underlying spot price and twice to volatility.

[edit] Vanna

$Vanna = \frac{\partial \Delta}{\partial \sigma} = \frac{\partial^2 V}{\partial S \partial \sigma}$

Vanna, also referred to as DvegaDspot and DdeltaDvol^[11], measures the sensitivity of the option vega with respect to change in the underlying spot price. Vanna is a second order derivative of the option value; once to the underlying spot price and once to volatility and is mathematically equivalent to DdeltaDvol^[12]: the sensitivity of the option delta with respect to change in volatility. Vanna can be a useful sensitivity to monitor when maintaining a delta- or vega-hedged portfolio as vanna will help the trader to anticipate changes to the effectiveness of a delta-hedge as volatility changes or the effectiveness of a vega-hedge against change in the underlying spot price.

[edit] Vega

$\nu=\frac{\partial V}{\partial \sigma}$

Vega, is not actually a Greek letter (The Greek letter nu, 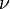$\nu\,$ is used instead). Vega measures sensitivity to volatility. Vega is the derivative of the option value with respect to the volatility of the underlying. The term kappa, $κ$ , is sometimes used (by academics) instead of vega, as is tau, $τ$ , though this is rare.

[edit] Practical use

Vega is typically expressed as the amount of money, per underlying share the option's value will gain or lose as volatility rises or falls by 1%.

Vega can be an important Greek to monitor for an option trader, especially in volatile markets since some the value of option strategies can be particularly sensitive to changes in volatility. The value of an option straddle, for example, is extremely dependant on changes to volatility.

[edit] Vomma

$Vomma = \frac{\partial \nu}{\partial \sigma} = \frac{\partial^2 V}{\partial \sigma^2}$

Vomma^[13], Volga^[14], Vega Convexity^[15] or Vega gamma measures second order sensitivity to implied volatility. Volga is the second derivative of the option value with respect to the volatility, or, stated another way, volga measures the rate of change to vega as volatility changes.

[edit] Zomma

$Zomma = \frac{\partial \Gamma}{\partial \sigma} = \frac{\partial^3 V}{\partial S^2 \partial \sigma}$

Zomma measures the rate of change of gamma with respect to changes in volatility. Zomma has also been referred to as DgammaDvol^[16]. Zomma is the third derivative of the option value, twice to underlying asset price and once to volatility. Zomma can be a useful sensitivity to monitor when maintaining a gamma-hedged portfolio as zomma will help the trader to anticipate changes to the effectiveness of the hedge as volatility changes.

[edit] Black-Scholes

The Greeks under the Black-Scholes model are calculated as follows, where $φ$ (phi) is the standard normal probability density function and $Φ$ is the standard normal cumulative distribution function. Note that the gamma and vega formulas are the same for calls and puts.

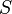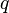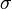For a given: Stock Price $S \,$ , Strike Price $K \,$ , Risk-Free Rate $r \,$ , Annual Dividend Yield $q \,$ , Time to Maturity, $\tau = T-t \,$ , and Volatility $\sigma \,$ ...

	Calls	Puts
value	$e^{-q \tau} S\Phi(d_1) - e^{-r \tau} K\Phi(d_2) \,$	$e^{-r \tau} K\Phi(-d_2) - e^{-q \tau} S\Phi(-d_1) \,$

delta	$e^{-q \tau} \Phi(d_1) \,$	$-e^{-q \tau} \Phi(-d_1)\,$
vega	$S e^{-q \tau} \phi(d_1) \sqrt{\tau} = K e^{-r \tau} \phi(d_2) \sqrt{\tau} \,$
theta	$-e^{-q \tau} \frac{S \phi(d_1) \sigma}{2 \sqrt{\tau}} - rKe^{-r \tau}\Phi(d_2) + qSe^{-q \tau}\Phi(d_1) \,$	$-e^{-q \tau} \frac{S \phi(d_1) \sigma}{2 \sqrt{\tau}} + rKe^{-r \tau}\Phi(-d_2) - qSe^{-q \tau}\Phi(-d_1) \,$
rho	$K \tau e^{-r \tau}\Phi(d_2)\,$	$-K \tau e^{-r \tau}\Phi(-d_2) \,$

gamma	$e^{-q \tau} \frac{\phi(d_1)}{S\sigma\sqrt{\tau}} \,$
vanna	$-e^{-q \tau} \phi(d_1) \frac{d_2}{\sigma} \, = \frac{\nu}{S}\left[1 - \frac{d_1}{\sigma\sqrt{\tau}} \right]\,$
charm	$-qe^{-q \tau} \Phi(d_1) + e^{-q \tau} \phi(d_1) \frac{2(r-q) \tau - d_2 \sigma \sqrt{\tau}}{2\tau \sigma \sqrt{\tau}} \,$	$qe^{-q \tau} \Phi(-d_1) + e^{-q \tau} \phi(d_1) \frac{2(r-q) \tau - d_2 \sigma \sqrt{\tau}}{2\tau \sigma \sqrt{\tau}} \,$

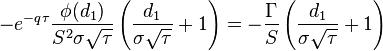speed	$-e^{-q \tau} \frac{\phi(d_1)}{S^2 \sigma \sqrt{\tau}} \left(\frac{d_1}{\sigma \sqrt{\tau}} + 1\right) = -\frac{\Gamma}{S}\left(\frac{d_1}{\sigma\sqrt{\tau}}+1\right) \,$
zomma	$e^{-q \tau} \frac{\phi(d_1)\left(d_1 d_2 - 1\right)}{S\sigma^2\sqrt{\tau}} = \Gamma\left(\frac{d_1 d_1 -1}{\sigma}\right) \,$
color	$-e^{-q \tau} \frac{\phi(d_1)}{2S\tau \sigma \sqrt{\tau}} \left[2q\tau + 1 + \frac{2(r-q) \tau - d_2 \sigma \sqrt{\tau}}{\sigma \sqrt{\tau}}d_1 \right] \,$

DvegaDtime	$Se^{-q \tau} \phi(d_1) \sqrt{\tau} \left[ q + \frac{ \left( r - q \right) d_1 }{ \sigma \sqrt{\tau} } - \frac{1 + d_1 d_2}{2 \tau} \right] \,$
vomma	$Se^{-q \tau} \phi(d_1) \sqrt{\tau} \frac{d_1 d_2}{\sigma} = \nu \frac{d_1 d_2}{\sigma} \,$

dual delta	$-e^{-r \tau} \Phi(d_2) \,$	$e^{-r \tau} \Phi(-d_2) \,$
dual gamma	$e^{-r \tau} \frac{\phi(d_2)}{K\sigma\sqrt{\tau}} \,$

where

$d_1 = \frac{\ln(S/K) + (r - q + \sigma^2/2)\tau}{\sigma\sqrt{\tau}}$

$d_2 = \frac{\ln(S/K) + (r - q - \sigma^2/2)\tau}{\sigma\sqrt{\tau}} = d_1 - \sigma\sqrt{\tau}$

$\phi(x) = \frac{e^{- \frac{x^2}{2}}}{\sqrt{2 \pi}}$

$\Phi(x) = \frac{1}{\sqrt{2\pi }} \int_{-\infty}^x e^{- \frac{y^2}{2}} \,dy = \frac{1}{\sqrt{2\pi }} \int_{-x}^{\infty} e^{- \frac{y^2}{2}} \,dy$

[edit] References

^ Banks, Erik; Siegel, Paul (2006). The options applications handbook: hedging and speculating techniques for professional investors. McGraw-Hill Professional. p. 263. ISBN 0071453156, 9780071453158.
^ Macmillan, Lawrence G. (1993). Options as a Strategic Investment (3rd ed.). New York Institute of Finance. p. 742. ISBN 0-13-636002-5 0-13-099661-0.
^ Chriss, Neil (1996). Black-Scholes and beyond: option pricing models. McGraw-Hill Professional. p. 308. ISBN 0786310251, 9780786310258.
^ Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 51
^ This author has only seen this referred to in the English spelling "Colour", but has written it here in the US spelling to match the style of the existing article.
^ Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 56
^ Espen Gaarder Haug, "Know Your Weapon, Part 2", Wilmott Magazine, July/August 2003, p. 53
^ Macmillan, Lawrence G. (1993). Options as a Strategic Investment (3rd ed.). New York Institute of Finance. p. 799. ISBN 0-13-636002-5.
^ Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 55
^ Haug, Espen Gaardner (2007). The Complete Guide to Option Pricing Formulas. McGraw-Hill Professional. ISBN 0071389970, 9780071389976.
^ Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 51
^ Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 51
^ Espen Gaarder Haug, "Know Your Weapon, Part 2", Wilmott Magazine, July/August 2003, p. 52
^ Espen Gaarder Haug, "Know Your Weapon, Part 2", Wilmott Magazine, July/August 2003, p. 52
^ Espen Gaarder Haug, "Know Your Weapon, Part 2", Wilmott Magazine, July/August 2003, p. 52
^ Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 55

[edit] See also

[edit] External links

Why We Have Never Used the Black-Scholes-Merton Option Pricing Formula, Nassim Taleb and Espen Haug
Surface Plots of Black-Scholes Greeks: Chris Murray
Delta: quantnotes.com,
Delta, Gamma, GammaP, Gamma symmetry, Vanna, Speed, Charm, Saddle Gamma: Vanilla Options - Espen Haug,
Volga, Vanna, Speed, Charm, Color: Vanilla Options - Uwe Wystup, Vanilla Options - Uwe Wystup
Online real-time option prices and Greeks calculator when the underlying is normally distributed, by Razvan Pascalau, Univ. of Alabama

[0] Banks, Erik; Siegel, Paul (2006). The options applications handbook: hedging and speculating techniques for professional investors. McGraw-Hill Professional. p. 263. ISBN 0071453156, 9780071453158.

[1] Macmillan, Lawrence G. (1993). Options as a Strategic Investment (3rd ed.). New York Institute of Finance. p. 742. ISBN 0-13-636002-5 0-13-099661-0.

[2] Chriss, Neil (1996). Black-Scholes and beyond: option pricing models. McGraw-Hill Professional. p. 308. ISBN 0786310251, 9780786310258.

[3] Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 51

[4] This author has only seen this referred to in the English spelling "Colour", but has written it here in the US spelling to match the style of the existing article.

[5] Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 56

[6] Espen Gaarder Haug, "Know Your Weapon, Part 2", Wilmott Magazine, July/August 2003, p. 53

[7] Macmillan, Lawrence G. (1993). Options as a Strategic Investment (3rd ed.). New York Institute of Finance. p. 799. ISBN 0-13-636002-5.

[8] Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 55

[9] Haug, Espen Gaardner (2007). The Complete Guide to Option Pricing Formulas. McGraw-Hill Professional. ISBN 0071389970, 9780071389976.

[10] Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 51

[11] Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 51

[12] Espen Gaarder Haug, "Know Your Weapon, Part 2", Wilmott Magazine, July/August 2003, p. 52

[13] Espen Gaarder Haug, "Know Your Weapon, Part 2", Wilmott Magazine, July/August 2003, p. 52

[14] Espen Gaarder Haug, "Know Your Weapon, Part 2", Wilmott Magazine, July/August 2003, p. 52

[15] Espen Gaarder Haug, "Know Your Weapon, Part 1", Wilmott Magazine, May 2003, p. 55

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

Greeks (finance)

From Wikipedia, the free encyclopedia

Contents

[edit] Use of the Greeks

[edit] Charm

[edit] Practical use

[edit] Color

[edit] Practical use

[edit] Delta

[edit] Practical use

[edit] As a proxy for probability

[edit] Relationship between call and put delta

[edit] DvegaDtime

[edit] Practical use

[edit] Lambda

[edit] Gamma

[edit] Rho

[edit] Practical use

[edit] Speed

[edit] Theta

[edit] Practical use

[edit] Ultima

[edit] Vanna

[edit] Vega

[edit] Practical use

[edit] Vomma

[edit] Zomma

[edit] Black-Scholes

[edit] References

[edit] See also

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages